

Детская энциклопедия
ДЭ, том 2 Мир небесных тел. Числа и фигуры
Часть II
Том 2 Содержание
Предыдущий раздел
Юный математик.
«Поединок».
Если спросить всех школьников, какой предмет нравится им больше других, то вряд ли большинство из них назовут математику. Обычно ее скорее уважают, чем любят. У нас в стране научные знания пользуются большим почетом, но, конечно, и среди наших школьников есть такие, которые тяготятся изучением математики. По-видимому, дело объясняется не только тем, что ее изучение многим нелегко дается и требует упорства и труда, но также и тем, что некоторые вопросы школьной математики иногда кажутся недостаточно интересными и даже порой скучными. Однако азбука и грамматика какого-либо языка часто также не очень интересны, а между тем только через их изучение лежит путь ко всей литературе с ее увлекательными сказками, рассказами, повестями, романами и стихами. Подобно этому, через те простейшие, азбучные положения математики, которые изучаются в школе, лежит столбовая дорога к современной математике - огромной, почти необозримой по своему богатству области человеческого знания, которая находит с каждым годом все большее применение.
Иногда приходится слышать мнение, что в математике в основном все уже известно, что времена открытий в этой науке давно прошли, а теперь остается только изучать теоремы, названные именами ученых прошлых веков, и применять их к решению разных задач. Но в действительности это далеко не так. Даже более того, именно сейчас математика переживает период чрезвычайно бурного развития, несмотря на то что родилась она много тысячелетий назад. Новые математические открытия в наши дни делаются буквально ежедневно во всех частях света. Чтобы получить представление о количестве этих открытий, достаточно знать следующее. В Советском Союзе издается ежемесячный реферативный журнал «Математика», в котором убористым шрифтом печатаются самые краткие сообщения (рефераты) о различных математических открытиях, сделанных в самое последнее время во всем мире. Так вот, комплект этого журнала за 1963 г. представляет собой огромный том (свыше 1100 страниц большого формата!), содержащий более 16 000 рефератов. Так велико число математических открытий, сделанных всего за один год: в среднем по 45 открытий в день! Конечно, не все они одинаково значительны, но все-таки почти каждое из них означает продвижение науки вперед, пусть иногда даже на совсем маленький шажок.
Такое бурное развитие математики тесно связано с тем, что теория и практика выдвигают все новые и новые задачи, которые математики должны решать. И вот когда старых знаний не хватает, приходится изобретать новые пути, находить новые методы. Ныне математика применяется не только в астрономии, механике, физике, химии и технике, где она применялась и раньше, но также в биологии, некоторых отраслях обще-
261
ственных наук и даже в языкознании. Особенно большое поле для ее применений открылось в связи с созданием быстродействующих электронных вычислительных машин. Они предсказывают погоду, вычисляют орбиты искусственных спутников, космических кораблей, переводят научные тексты с одного языка на другой.
В ближайшее время новые типы вычислительных универсальных и специализированных машин еще более широко будут применяться в самых разнообразных областях человеческой деятельности, в том числе для управления производственными процессами, для статистического и бухгалтерского учета, плановых и проектных расчетов.
Коротко математику можно охарактеризовать как науку о числах и фигурах. Трудно назвать такую отрасль человеческой деятельности, где не приходилось бы ставить и решать вопросы о количестве предметов, об их размерах и форме. С глубокой древности, по мере развития человеческого общества, накапливалось все больше сведений о числах, о размерах и формах различных предметов. Появилась необходимость приводить эти сведения в порядок, чтобы их легче было передавать от одного поколения другому. Так постепенно зарождалась математика.
Начатки математических знаний обнаруживаются уже примерно за 4 тыс. лет до н. э. Об этом свидетельствуют дошедшие до нас египетские папирусы, клинописные вавилонские таблички, где встречаются решения различных арифметических, геометрических и алгебраических задач.
Большого расцвета математика достигла в древней Греции. Более чем за 300 лет до н. э. здесь появились «Начала» Евклида - сочинение, в котором систематически излагалась геометрия в том примерно объеме, в каком она доныне изучается в средней школе, а также давались сведения о делимости чисел и о решении квадратных уравнений (в геометрической форме). В III в. до н. э. Архимед нашел способ определения площадей,
Современная математика на службе народного хозяйства. На снимке показан внешний вид электронной вычислительной машины БЭСМ-2.
262
объемов и центров тяжести простых фигур. В конце III в. до н. э. Аполлоний написал книгу о свойствах некоторых замечательных кривых - эллипса, гиперболы и параболы. Если к этому добавить еще, что во II в. н. э. Птолемей в астрономическом сочинении, известном под арабским названием «Альмагест», изложил основы тригонометрии, дал таблицы синусов (вернее, длин хорд окружности) и способы решения сферических треугольников (т. е. треугольников, сторонами которых являются дуги больших кругов, проведенных на шаре), то станет ясно, какой большой вклад в развитие математических знаний внесли древние греки за много столетий до нашего времени. Можно смело утверждать, что нынешние школьники изучают за все время пребывания в средней школе лишь небольшую часть этих знаний (правда, они получают также и ряд сведений, которые древним грекам были неизвестны).
Много сделали для развития математики ученые народов Востока (особенно больших успехов добились индийцы и арабы в развитии алгебры и тригонометрии). Ученым Западной Европы после длительного застоя в развитии науки во времена средневековья пришлось затратить немало усилий, чтобы усвоить труды их предшественников. Лишь после этого они смогли двигаться вперед самостоятельно. Расцвет математики в Европе начинается к XVII в. В это время зарождаются новые отрасли математики, которые относятся к так называемой высшей математике и изучаются ныне в высших учебных заведениях. Особенно глубоко высшая математика изучается на физико-математических факультетах университетов и педагогических институтов, некоторые ее разделы изучаются в высших технических учебных заведениях.
Основу высшей математики составляют аналитическая геометрия и дифференциальное и интегральное исчисления. Их создание, связанное с именами великих ученых XVII в.- Р. Декарта, П. Ферма, И. Ньютона
263
и Г. Лейбница, позволило математически изучать движение, процессы изменения величин и геометрических фигур. Вместе с этим в математику вошли координаты, переменные величины и понятие функции. С координатами, переменными величинами и функциями школьники знакомятся при изучении алгебры и тригонометрии. Но при этом они остаются лишь у порога той высшей математики, которая в течение последних трехсот лет проявила себя как незаменимый инструмент исключительной силы и тонкости, позволивший сменяющим друг друга поколениям астрономов, физиков, механиков и представителям других областей науки решать труднейшие проблемы естествознания и техники.
Невозможно проследить здесь, хотя бы и бегло, успехи математики за последние столетия. Отметим большой вклад, внесенный русскими учеными Н. И. Лобачевским, П. Л. Чебышевым и советскими математиками. Можно сказать, что современная математика достигла такой степени развития и так богата содержанием, что одному человеку, даже самому ученому, нельзя охватить ее всю и приходится специализироваться в какой-либо определенной ее области.
Надо заметить, что современная математика состоит не только из алгебры и геометрии, как школьный курс; сейчас насчитывается несколько десятков различных областей математики, каждая из которых имеет свое особое содержание, свои методы и области применения.
В разделе тома, посвященном математике и названном «Числа и фигуры», мы поместили несколько статей, тесно связанных со школьным курсом математики, дополняющих и углубляющих те знания, которые читатель уже имеет. Но мы считали необходимым также приподнять завесу, отделяющую элементарную, школьную математику от математики высшей.
Мы понимаем, что некоторые из наших статей нельзя назвать простыми и легкодоступными. Мы советуем при чтении таких статей вооружиться терпением, а также бумагой и карандашом и одолевать их шаг за шагом. Если читатель и тут потерпит неудачу - отчаиваться не следует. Можно вспомнить слова, с которыми знаменитый французский математик Ж. Лагранж обращался к молодым математикам: «Читайте, понимание придет потом».
Во всяком случае, мы надеемся, что каждый любитель математики найдет здесь такие статьи, которые будут для него сразу же доступны. Что касается остальных, то к ним можно обратиться позже, когда читатель продвинется вперед в школьном курсе. Словом, понимание придет!
ЧИСЛА
Все числа мы привыкли записывать с помощью десяти знаков-цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Например, число, состоящее из четырех сотен, четырех десятков и четырех единиц, мы записываем так: 444. При этом один и тот же знак «4» обозначает число единиц, если он стоит на последнем месте, число десятков - если на предпоследнем, и число
десятков десятков, т. е. сотен, если он стоит на третьем месте от конца. Такой принцип записи чисел называется позиционным или поместным, потому что каждая цифра получает числовое значение не только в зависимости от своего начертания, но и от того, на каком месте она стоит при записи числа. Позиционный принцип позволяет с помощью десяти знаков-цифр записать любое сколь угодно большое число. Действительно, пусть нам дано целое число N. Для того чтобы записать его в нашей системе, находим сначала остаток от деления N на 10, затем остаток от деления
265
частного на 10 и т. д.- до тех пор, пока в качестве частного не получим числа, меньшего 10. Например:
N =523=10·52+3; 52=10·5+2; 5=10·0+5.
Полученные остатки и являются последовательными цифрами нашего числа, записанного в позиционной десятичной системе:
N=523, или, более подробно:
N=5·10² +2· 10 +3.
Для тех, кто знаком с алгеброй, скажем, что каждое целое число М можно представить в таком же виде. Если
10n ≤ М< 10n +1, то
M = an 10n +an _1 10n-1 +... a1 10+а0,
где каждый из коэффициентов а0, a1, ..., аn меньше 10 (это просто остатки от последовательного деления числа М на 10). Следовательно, каждый из коэффициентов выразится одной из десяти цифр. Следуя десятичному позиционному принципу, записываем число М так:
М = аn аn-1 ...а1 a0,
где а0 означает число обычных единиц, или единиц первого разряда, содержащихся в М, а1 - число единиц второго разряда, т. е. десятков, а2 - число единиц третьего разряда, т. е. сотен, и т. д.
Число 10 называется основанием нашей системы.
Итак, для записи чисел мы пользуемся десятичной позиционной системой счисления.
Однако вовсе не обязательно считать десятками. Можно, например, вести счет двойками или тройками. Для этого за основание системы счисления примем число 2 или 3, а в остальном будем поступать точно так же, как это делали, когда основание равнялось десяти. Для записи по двоичной системе понадобятся всего две цифры: 0 и 1. Число «два» в этой
системе запишется как 10, так как 2=1·2+0.
Таблица сложения
А чтобы не спутать нашу запись с обычной, будем справа внизу ставить маленькую цифру2 - это будет означать, что основанием системы служит число «два». Итак, 102 будет записью числа 2. Число 3=1·2+1, поэтому его записью будет 112 .
Число 4 = 1·2² +0·2+0·1, поэтому оно запишется в виде 1002. Записью числа 5 будет 1012, а числа 7 будет 1112 .
Чтобы найти запись любого числа N, нужно определить остатки от последовательного деления этого числа на 2. Мы предоставляем читателям проверить, что записью числа 35 в двоичной системе будет 100 0112 .
Если число N таково, что
2n £ N<2n+1, то его можно представить в виде:
N = аn 2 n + аn-1 2n-1 +... +а1 2 + а0,
т. е. запись этого числа в двоичной системе будет иметь вид:
N=an an _1 ...a1 a0,
но здесь уже каждый из коэффициентов аi может принимать только два значения: 0 или 1.
Более подробно о двоичной системе, которая сейчас приобрела большое значение в связи с ее применением в быстродействующих вычислительных машинах, узнаете, если прочтете статью «Электронные вычислительные машины», помещенную в этом томе.
Для записи числа в троичной системе нужны три цифры, например 0, 1, 2. Число 3 здесь будет записываться как 103, а 4 - как 113. Записью числа 35 в той системе будет 10223 .
Приведем таблицы сложения и умножения чисел, записанных по троичной системе:
Таблица умножения
Но можно считать и дюжинами, т. е. пользоваться системой счисления с основанием двенадцать. Еще не так давно в нашей стране и в Западной Европе некоторые предметы, например перья и карандаши, принято было считать дюжинами. Сервизы тоже обычно составляют из 12 чашек, 12 блюдец, 12 тарелок, а комплек-
266
ты мебели - из 12 стульев или кресел. Существовало даже специальное название для дюжины дюжин - гросс.
О широком распространении двенадцатеричной системы свидетельствуют такие факты: мы до сих пор делим год на 12 месяцев, а сутки на 24 часа, причем в повседневной жизни часы считаем только до 12, а затем начинаем счет сначала (час дня, два часа дня и т. д.). Число 12 часто встречается также в сказках и легендах (двенадцатиглавый змей, двенадцать братьев-разбойников), что тоже свидетельствует о древнем происхождении двенадцатеричной системы счисления.
Посмотрим, как будут изображаться числа в этой системе. Во-первых, в ней должно быть двенадцать цифр. Значит, к нашим десяти цифрам надо прибавить еще две, например А для обозначения десяти и Б - для одиннадцати. Во-вторых, запись чисел в ней будет короче, чем в нашей системе, а таблица умножения длиннее. Число 12 запишется как 1012 (снова ставим значок12 для того, чтобы знать, в какой системе сделана запись), число 13 - как 1112, число 35=2·12+11 - как 2 Б12, а число 133 = 11·12+ +1 - как Б112, т. е. оно станет двузначным. Приведем таблицу умножения чисел, записанных в этой системе1 :
Некоторые ученые считали, что такая система была бы удобнее, чем десятичная, так как число 12 имеет больше делителей, чем число 10. На самом же деле это обстоятельство не дает больших преимуществ.
Ниже мы расскажем о том, что когда-то существовали нумерации с основанием 20 и даже 60.
¹ При записи этой таблицы мы опускаем значок 12. Но не надо забывать, что все числа записаны в двенадцатеричной системе.
А теперь сделаем некоторые общие выводы: 1) всякое число, отличное от единицы, может служить основанием позиционной системы счисления; 2) в системе счисления должно быть столько цифр, сколько единиц содержится в основании системы.
Несмотря на то что принципиально все позиционные системы счисления равноправны, в разных случаях удобнее пользоваться разными системами. Например, как мы уже говорили, при счете на электронных вычислительных машинах в основном пользуются двоичной системой.
Сейчас мы приведем несколько задач, для решения которых удобнее будет воспользоваться не десятичной системой счисления, а другими.
Вот одна из классических задач, решить которую можно сразу же, если выбрать систему счисления с подходящим основанием. Эта задача приведена в математической книге знаменитого математика XIII в. Леонардо Пизанского. Ею интересовался также в XVIII в. и Л. Эйлер.
Требуется выбрать 5 гирь так, чтобы с их помощью можно было взвесить любой груз до 30 кГ при условии, что гири ставятся только на одну чашу весов.
Какие же гири нужно выбрать?
Сумма веса всех гирь должна быть не меньше 30 кГ. Но, конечно, этого недостаточно. Если мы выберем, например, гири весом в 1, 2, 3, 10, и 15 кГ, то с их помощью нельзя будет взвесить грузы в 7, 8, 9, 22, 23 и 24 кГ.
Разберем математический смысл задачи. Чтобы взвесить некоторый груз, помещая гири только на одну чашу весов, надо представить его вес в виде суммы весов имеющихся гирь, причем так, чтобы каждая гиря бралась не более одного раза. Если выбранные нами гири имеют вес p1 , р2, р3, р4, р5, то груз весом Q £ 30 кГ должен представляться так:
Q=a1 p1 + а2 p2 + а3 р3 + а4 p4 + a5 p5,
где каждый коэффициент равен единице, если кладем соответствующую гирю на чашу весов, и нулю, если не пользуемся ею при взвешивании.
При такой постановке вопроса видно сходство с представлением числа Q в двоичной системе счисления. Нужно только в качестве p1, p2. p3, p4, p5 взять гири весом: р1 =1 кГ, р2 =2 кГ, p3 =4 кГ, р4 =8 кГ, р5 =16 кГ.
267
Сумма их веса 1 +2+4+8+16=31>30 кГ. Кроме того, каждое число Q, не большее 31, можно представить в виде:
Q = b4 24 + b3 2³ + b2 2² + b1 2 + b0,
где каждый из коэффициентов b0, b1 b2, b3, b4 будет, как нам и нужно, либо нулем, либо единицей.
Пусть, например, надо взвесить груз в 22 кГ. Запишем число 22 по двоичной системе:
22 = 101102 .
Значит, нужно взять гири р2 =2 кГ ', р3 = 4 кГ и р5 = 16 кГ.
Теперь несколько видоизменим задачу: пусть требуется выбрать 4 гири, с помощью которых можно было бы взвесить любой груз до 40 кГ, при условии, что гири можно класть и на левую и на правую чашу весов.
Нетрудно убедиться, что для решения этой задачи нужно воспользоваться троичной системой счисления, т. е. выбрать следующие 4 гири: р1 = 1 кГ, р2 = 3 кГ, р3 = 9 кГ, р4 = 27 кГ.
Пусть, например, надо взвесить груз в 19 кГ. Число 19 представим в виде:
19 = 3·6 + 1 = 3·(3·2)+1=2·9+1=0·27+2·9+0·3+1=2013 .
Теперь груз в 19 кГ кладем на правую чашу весов. На левую кладем груз в 1 кГ. Затем надо было бы положить туда еще 2 гири по 9 кГ, но у нас имеется только одна такая гиря.
Но 18=2·9 можно представить еще и иначе: 18=2·9=(3-1)·9=27-9,
т. е. на левую чашу весов надо положить еще гирю в 27 кГ, на правую - в 9 кГ.
Так же будем поступать и в других случаях. Если груз Q £ 40 кГ, то его можно всегда представить в виде:
Q = b3 3³ + b2 3² + b1 3+ b0,
где каждый из коэффициентов b0, b1, b2, b3 может равняться 0, 1 или 2. Если он равен О, то соответствующую гирю отставляем в сторону; если 1, то кладем ее на левую чашу весов; если 2, то поступаем так, как только что делали, т. е. кладем гирю на правую чашу весов, а следующую по величине гирю - на левую. Следует помнить, что, хотя в различных системах счисления числа записываются по-разному, основные свойства их от этого не меняются: так, число 20 будет делиться на 2, в какой бы системе мы его ни записали, а 27 не будет делиться на 2, но будет делиться на 3. Числа 3, 5, 7 останутся простыми в любых системах счисления. Однако признаки делимости, которые устанавливаются исходя из записи числа в определенной системе счисления, будут меняться вместе с основанием системы. Так, число делится на 5, если его запись по десятичной позиционной системе оканчивается нулем или пятеркой. Но число не всегда делится на 5, если на 0 оканчивается его запись в троичной системе, например числа 103 (т. е. 3), 1003 (т. е. 9), 10003 (т. е. 27) не делятся на 5, а число 1203 (т. е. 15) будет делиться на 5.
И русский, и француз, и немец одно и то же число назовут по-разному (на своем языке), а запишут его одинаково.
268
Теперь, естественно, возникает вопрос: почему мы все-таки пользуемся десятичной системой, а не системой с другим основанием? И еще: всегда ли люди записывали числа, пользуясь позиционным принципом?
На эти вопросы мы и постараемся дать ответ.
Чтобы лучше понять, как люди считали в старину, обратимся сначала к. нашей речи, к нашему устному счету. Прежде всего заметим, что наш устный счет очень отличается от письменного.
Как мы называем число 444? Мы говорим: «Четыреста сорок четыре», т. е. произносим три разных слова. В то же время это число записываем тремя одинаковыми знаками. Если то же самое число нужно будет записать немцу или французу, то они напишут такие же три знака, а произнесет каждый из них различные слова: один - по-немецки, другой - по-французски.
Итак, наша письменная нумерация носит международный характер, тогда как названия числительных и способы их образования у разных народов различны. Но дело не только в этом. Давайте рассмотрим более подробно, как мы называем числа.
Для нуля и первых девяти чисел мы употребляем специальные названия: «нуль», «один», «два»,..., «девять». Для следующего числа у нас есть новое слово - «десять»; мы не говорим «один, нуль», хотя и записываем его с помощью единицы и нуля: 10.
Все числа от 11 до 99, как правило, составляются из названий первых чисел: «одиннадцать» (т. е. один-на-десять), «тридцать один» (т. е. три-десять-один) и т. д. Для 100 мы употребляем новое слово - «сто». Все наименования чисел от 101 до 999 опять составные, а для 1000 вводится новое слово - «тысяча». Далее тоже идут новые слова: «миллион», «миллиард», «триллион» и т. д. Как видим, по мере роста самих чисел возрастает и количество названий для них. Из этого явствует, что способ наименования чисел не является позиционным. Наш устный счет сохранил следы каких-то более старых нумераций, одной из которых мы и сейчас пользуемся при записи чисел по римской системе. В римской системе имеются специальные знаки для единицы (I), пяти (V), десяти (X), пятидесяти (L), ста (С), пятисот (D) и тысячи (М). Остальные числа записываются при помощи этих символов с применением сложения и вычитания: III, например, есть запись числа три (I+I+I), IV - числа четыре (V-I),
VI - числа шесть (V+I) и т. д. Наше число 444 запишется в римской системе так: GDXLIV. Эта форма записи менее удобна, чем та, которой мы теперь пользуемся. Здесь четыре единицы записываются одними символами (IV), четыре десятка - другими (XL), четыре сотни -
Цифры в древнем Риме.
третьими (CD). Запись чисел получается намного длиннее. Но не только в этом дело: с числами, записанными в римской нумерации, очень трудно производить арифметические действия. Попробуйте, например, перемножить 444 на 36, если оба числа обозначены римскими цифрами, и вы сразу же убедитесь в трудности задачи. Сами римляне пользовались для производства арифметических операций специальной счетной доской - абаком.
В римской системе есть и еще один существенный недостаток: она не дает способа для
Так написали бы 444 древние египтяне.
записи сколь угодно больших чисел. Например, чтобы написать по этой системе 1 000 000, надо либо 1000 раз повторить знак М, либо ввести новый символ. Таким образом, для записи чисел по мере их роста надо будет вводить все
269
новые и новые знаки. Это происходит потому, что римская нумерация не является позиционной. Знак V, например, означает в ней только пять единиц и не может обозначать пяти десятков или пяти сотен. Римская нумерация не является и строго десятичной. В ней сохранились следы другого основания - пяти. Действительно, здесь есть специальные знаки для пяти, пятидесяти и пятисот.
В нашем устном счете имеются некоторые черты, напоминающие эту систему. Так, мы тоже прибегаем к операции сложения, образуя числительные от 11 до 19: «одиннадцать» (один-на-десять) и т. д. Но начиная с 20 пользуемся для образования числительных еще и умножением, чего нет в римской системе: «двадцать» означает два-десять, т. е. два X десять, «тридцать» - три X десять.
В нашем языке сохранились также следы нумерации с основанием 40, которой пользовались наши предки. Действительно, для этого числа употребляется новое, несоставное название - «сорок». Нам известны такие выражения:
«сорок сороков церквей», «сорок сороков черных соболей». О том, что число 40 когда-то играло особую роль при счете, говорят и некоторые связанные с ним поверья. Так, сорок первый медведь считался роковым для охотника. Аналогично этому широко распространен у европейских народов предрассудок, будто число 13 является несчастливым. Это связано с тем, что некогда была распространена двенадцатеричная система счисления.
Во французском языке сохранились следы нумерации с основанием 20; число 80 читается: quatre-vingts - «четыре-двадцать», число 90-
quatre-vingts-dix - «четыре-двадцать-десять»,
число 120 - «шесть-двадцать»; в старофранцузском языке и другие названия чисел составлялись аналогичным образом. Следы двадцатеричной системы сохранились также в английском и голландском языках, следы пятеричной - в скандинавских языках.
Итак, устная речь показывает, что наши предки пользовались непозиционной нумерацией, причем в качестве оснований, кроме десяти, были и другие числа.
На основании каких же источников можно ответить на вопрос: как люди считали в старину?
Во-первых, на земном шаре сохранились народы, которые еще недавно стояли во многих отношениях на таком же низком уровне развития, как и наши далекие предки. Многие путешественники описали немало способов счета, применявшихся у таких народов. Это - один источник, с которым мы познакомимся.
Вторым источником являются письменные документы древних народов: египтян, вавилонян, древних греков, индейцев племени майя и других. Наконец, русские рукописи XI - XII вв. помогут нам узнать, как считали раньше на Руси. Итак, начнем по порядку.
Еще недавно существовали племена, в языке которых были названия только двух чисел: «один» и «два». Но это не значит, конечно, что представители этих племен не могли сосчитать большее количество предметов.
У туземцев островов, расположенных в Торресовом проливе (отделяющем Новую Гвинею от Австралии), единственными числительными являлись «урапун» (один) и «окоза» (два). Островитяне считали так: «окоза-урапун» (три), «окоза-окоза» (четыре), «окоза-окоза-урапун» (пять) и «окоза-окоза-окоза» (шесть). О числах начиная с семи туземцы говорили «много», «множество». Таким образом, люди здесь освоили только небольшое количество целых чисел. Кстати, многие русские пословицы говорят о том, что именно так дело обстояло и у наших предков. Мы говорим: «У семи нянек дитя без глаза», «Семь бед - один ответ», «Семеро одного не ждут», «Семь раз отмерь, один раз отрежь». Здесь, очевидно, число «семь» употребляется в смысле «много»: у большого числа нянек дитя без глаза, много бед - один ответ и т. д.
Но вернемся к нашему рассказу.
270
Очень рано у людей появилась необходимость сообщать друг другу о том, что такое-то число предметов должно быть доставлено через столько-то дней или что каждое племя должно выставить такое-то число воинов. И даже те народы, у которых имелось только два числительных, умели в известном смысле «сосчитывать» довольно большое количество предметов. Вот как, по рассказу замечательного русского путешественника Н. Н. Миклухо-Маклая, поступали туземцы Новой Гвинеи: «Излюбленный способ счета состоит в том, что папуас загибает один за другим пальцы руки, причем издает определенный звук, например «бе-бе-бе...». Досчитав до пяти, он говорит «ибон-бе» (рука). Затем он загибает пальцы другой руки, снова повторяет «бе-бе...», пока не доходит до «ибон-али» (две руки). Затем он идет дальше, приговаривая «бе-бе», пока не доходит до «самба-бе» и «самба-али» (одна нога, две ноги). Если нужно считать дальше, папуас пользуется пальцами рук и ног кого-нибудь другого».
Итак, предметы при счете сопоставлялись обычно с пальцами рук и ног. При переговорах туземцу достаточно было сказать, например, что он дошел в своем счете до третьего пальца правой ноги. Чтобы отсчитать нужное количество предметов, счет начинали сначала, от первого пальца правой руки. При этом, отсчитывая каждый палец, одновременно отмечали и предметы. Островитяне Торресова пролива для такого пересчета употребляли не только пальцы, а и другие части тела (запястье, локоть, плечо), но всегда в определенном порядке. Так они могли пересчитывать до 33 предметов.
Суть этого способа заключается в том, что равночисленность некоторых совокупностей предметов устанавливалась при помощи сопоставления их с частями тела, а иногда и просто палочками. Разумеется, наиболее удобным «инструментом» пересчета являются пальцы, вследствие чего предметы при пересчете чаще всего группировали по пяти, по десяти и по двадцати. Этим и объясняется то, что основанием большинства сложившихся систем счисления является 10 (по числу пальцев на обеих руках), а иногда 5 или 20.
Со временем хозяйство племен становилось все более сложным и обширным. Чаще приходилось сосчитывать все большее количество различных предметов, и простое установление равночисленности при помощи счета на пальцах перестало удовлетворять людей.
Люди постепенно привыкали при счете располагать предметы устойчивыми группами по
два, по десяти или двенадцати. Появились специальные слова для обозначения таких устойчивых совокупностей предметов. Так, у туземцев Флориды слово «на-куа» означало 10 яиц, «на-банара» - 10 корзин. Но слово «на», которое, казалось бы, соответствует числу 10, отдельно не употреблялось. То же можно было наблюдать на островах Фиджи и Соломоновых, где имелись специальные названия для 100 челноков, 100 кокосовых орехов, 1000 кокосовых орехов и в то же время отвлеченных чисел не было. Числа являлись по существу именованными, это еще «числа-совокупности» конкретных предметов.
Но с течением времени такими устойчивыми «числами-совокупностями» начали обозначать не только данные предметы, а и другие, похожие на них. Например, «числа-совокупности», обозначающие определенное количество орехов, могли впоследствии употребляться для счета любых круглых предметов. Это привело к тому, что во многих языках первобытных народов образовалось несколько рядов числительных: одни употреблялись только для счета людей, другие - для подсчета круглых предметов, третьи - продолговатых и т. д. Например, у чишмиенов (Британская Колумбия) имелось семь видов числительных, каждый из них употреблялся для счета предметов определенного вида.
Однако у большинства народов числа, которыми считали «деньги», постепенно вытеснили все остальные. По-видимому, это произошло тогда, когда в качестве денег в основном служил скот: приходилось сосчитывать стада, обменивать на них другие предметы. Естественно, что числа, служившие для подсчета скота, получили наибольшее распространение: их все хорошо знали. Они-то и стали теми универсальными числами, которые позволили считать любые предметы.
Однако так образовались только те числа, которым соответствовали «числа-совокупности»: если счет велся десятками, то появились названия для десяти, десяти десятков (т. е. ста), десяти сотен (т. е. тысячи). Кроме того, индивидуальные названия получили, как правило, все числа, меньшие десяти. Что касается чисел 11, 12, ..., 19, 21 и т. д., то они составлялись из основных при помощи тех операций, которые первоначально фактически производились над пересчитываемыми предметами. Так, на языке кламатов (Северная Америка), а также племен Британской Колумбии для обозначения составных чисел употреблялись специальные глаголы. Например, индеец го-
271
ворил: «На дважды десять плодов я кладу сверху шесть»,- и это обозначало 26 плодов. Такая фраза полностью соответствует фактическому пересчету: индейцы располагали 10 предметов в ряд, с 11-го начинался новый ряд и т. д. А постепенно эти двигательные операции перешли в арифметические.
Хорошей иллюстрацией к такому способу счета служат обозначения чисел, принятые в XI - XVI вв. индейцами племени ацтеков (Мексика): единицу они обозначали точкой, двойку - двумя точками (см. рисунок) и т. д. до пяти .
Так в Мексике обозначали числа индейцы племени ацтеков в XI-XVI вв.
В запись числа шесть входила вертикальная черта, которая отделяла пять первых точек от шестой. Ясно, что здесь счет велся группами по пяти предметов. Черта отделяла одну такую группу от другой, причем сама черта никакого числа не обозначала.
Основной операцией для образования составных чисел было сложение, но наряду с этим применялось и вычитание, а иногда даже умножение. Например, в русском языке, как мы уже говорили, для образования числительных употребляются и сложение, и умножение (двадцать семь: дваХдесять+семь). В угро-финских языках применяется и вычитание: число 8 там произносится как «два-десять» (т. е. десять без двух), 80 - как «два-сто», 800 - «два-десять-сто» («десять-сто», т. е. тысяча, - принцип умножения!). Так происходило освоение натурального ряда чисел. Посмотрим теперь, какими были первые записи чисел и как люди оперировали числами.
Одна из древнейших нумераций - египетская. До нас дошли надписи, сохранившиеся внутри пирамид, на плитах и обелисках. Они состоят из картинок-иероглифов, которые изображают птиц, зверей, людей, части человеческого тела (глаза, ноги) и различные неодушевленные предметы. Такой способ письма вообще характерен для ранних ступеней культуры. Подобные письмена были у обитателей Центральной Америки - индейцев племени майя, в Перу. Расшифровка их представляет огромные трудности, так как часто неизвестны ни язык древних народов, ни значение отдельных иероглифов. Казалось бы, задача является неразрешимой. И все-таки многие надписи уже прочитаны! Сначала были разгаданы письмена древних египтян, затем - вавилонская клинопись. В 30-х годах нашего века были прочитаны долго не поддававшиеся расшифровке хеттские надписи. И, наконец, совсем недавно найден ключ к разгадке письмен индейцев племени майя и надписей с острова Пасхи.
Сохранились два математических папируса, позволяющие судить о том, как считали древние египтяне. Один из них хранится в Британском музее в Лондоне, а другой - в Музее изобразительных искусств им. А. С. Пушкина в Москве. Для записи чисел древние египтяне употребляли иероглифы, означающие (последовательно): единицу, десять, сто, тысячу, десять тысяч, сто тысяч (лягушка), миллион (человек с поднятыми руками), десять миллионов:
Полагают, что иероглиф для сотни изображает измерительную веревку, для тысячи - цветок лотоса, для десяти тысяч - поднятый кверху палец, а... для десяти миллионов - всю Вселенную. Все остальные числа составлялись из основных с помощью только одной операции - сложения. При этом запись производилась не слева направо, как у нас, а справа налево. Число 15, например, записывалось так:
А число 444 писали так:
Мы видим, что древнеегипетская нумерация похожа на римскую, только при записи чисел не употребляется вычитание. Знакомясь с римской нумерацией, мы убедились, что умножать
272
Цифры в древнем Египте.
числа, записанные в непозиционной системе, очень неудобно. Как же считали древние египтяне? Оказывается, умножение и деление они производили путем последовательного удвоения чисел. Пусть, например, надо умножить 19 на 37. Египтяне последовательно удваивали число 37, причем в правом столбце записывали результаты удвоения, а в левом - соответствующие степени двойки:
Удвоение продолжалось до тех пор, пока не оказывалось, что из числа левого столбца можно составить множитель (в нашем примере: 19 = 1+2+16). Египтяне отмечали соответствующие строки вертикальными черточками и складывали те числа, которые стоят в этих же строках справа. В данном случае надо сложить 37 + +74 + 592 = 703. Так получали произведение.
Если теперь число 703 нужно было разделить на 19, то египтяне начинали последовательно удваивать делитель и продолжали это до тех пор, дока числа правого столбца оставались меньше 703. Затем из чисел правого столбца они пытались составить делимое, и тогда сумма чисел в левом столбце давала делитель:
В данном случае 703 = 608+76+19, т. е. частное будет 1+4+32=37. Если бы делимое не
делилось без остатка на делитель, то его не удалось бы составить из чисел правого столбца. У нас получилось бы и частное и остаток.
Египетский способ умножения нетруден, но требует очень большого количества операций, даже при умножении двузначных чисел. Если бы пришлось перемножать таким способом трехзначные или четырехзначные числа, мы не могли бы обойтись без помощи машины. Заметим также, что для умножения и деления египтяне пользовались фактически представлением числа по двоичной системе.
Мы видели, что непозиционные нумерации малоудобны: запись чисел в них очень длинна, арифметические операции производить трудно. По мере развития торговли и ремесла эти неудобства становились все чувствительнее, и вот в Малой Азии, где были древнегреческие колонии, которые вели оживленную торговлю, в середине V в. до н. э. появилась система счисления нового типа, так называемая алфавитная нумерация. Ее обычно называют ионийской. В этой системе числа обозначались при помощи букв алфавита, над которыми ставились черточки: первые девять букв обозначали числа от 1 до 9, следующие девять - числа 10, 20, 30, ..., 90 и следующие девять - числа 100, 200, ..., 900. Таким образом можно было обозначать любое число до 999.
Для обозначения чисел 1000, 2000, ..., 9000 греки употребляли те же буквы, что и для чисел 1, 2, ..., 9, но только при их записи ставили косую черточку слева внизу. Как это делалось, видно из прилагаемого рисунка на стр. 274. Да-
а
лее, для числа 10 000 употреблялся знак М - это число называлось мириадой; две мириады,
т. е. 20 000, обозначались так: М. Этим способом можно было обозначить все числа до мириады мириад, т. е. до 108. Более высокие десятичные разряды уже не могли быть записаны в ионийской нумерации и не имели названия в древнегреческом языке.
Великий математик, механик и инженер древности Архимед (III в. до н. э.) посвятил целое сочинение тому, чтобы дать общий прием наименования сколь угодно больших чисел. Издавна у греков, как, впрочем, и у других народов, наглядным образом для представления об очень большом и даже неисчислимом количестве служило число песчинок. В народных
273
сказках, например, встречается «неразрешимая» задача: сосчитать звезды на небе, капли в море или песчинки на земле. Архимед показал, что такие задачи можно решить. Свое сочинение он так и назвал «Исчисление песка» («Псаммит»). В нем он построил систему счета, в которой имелись числа, не только превосходящие количество песчинок в его родной Сицилии, но и такие, которые больше числа песчинок во Вселенной, если даже считать, что Вселенная сплошь заполнена песком. Но что же понимали греки времен Архимеда под всей Вселенной? В своем сочинении Архимед, следуя за греческим астрономом Аристархом Самосским, полагал, что в центре Вселенной находится Солнце, а Земля и другие планеты вращаются вокруг него. Вселенная имеет форму сферы, на поверхности которой расположены неподвижные звезды. Это была первая гелиоцентрическая система мира.
Греческое алфавитное изображение чисел.
Для подсчета количества песчинок Архимед должен был, хотя бы приблизительно, определить размеры диаметров Вселенной и песчинки, а затем найти отношение их объемов. Архимед сделал это, опираясь на данные астрономии своего времени и на собственные исследования в этой области. Число песчинок, которое должно было у него при этом получиться, в нашей нумерации записывается так: 1063. Это очень большое число, и до Архимеда не было средств ни для записи, ни для наименования чисел такого порядка.
Чтобы решить поставленную задачу, Архимед поступает следующим образом: все числа, меньшие мириады мириад, т. е. все числа от 1 до 108 -1, он объединяет в первую октаду (т. е. восьмерицу) и называет их «первыми числами». Число 108 служит единицей второй октады, в которую входят все числа от 108 до 102·8 -1. Это - «вторые числа». Аналогично этому число 102·8 является единицей третьей октады, а числа от 102·8 до 103·8 -1 являются «третьими». Продолжая это построение, можно дойти до мириадо-мириадной октады, которая содержит числа от 10(10 8 -1) · 8 до 108·10 8 -1. Все эти октады Архимед объединяет в первый период. Число 108·10 8 служит единицей первой октады второго периода и т. д. Этим способом можно дойти до последнего числа последней октады мириадо-мириадного периода. Здесь Архимед останавливается, но ясно, что с помощью его способа можно двигаться и дальше, объединив все периоды в какой-нибудь новый разряд.
Но и тех чисел, которые построил Архимед, вполне достаточно для подсчета числа песчинок во Вселенной. Необходимое число содержится уже в восьмой октаде первого периода. Архимед продолжил свое построение дальше для того, чтобы разъяснить метод наименования сколь угодно больших чисел.
Способ Архимеда близок к позиционному, но понадобилось еще около тысячи лет, прежде чем человечеству удалось создать десятичную позиционную систему счисления.
Так записывались числа в древнеславянской нумерации.
Алфавитные системы были, кроме ионийцев, у древних евреев, финикийцев, армян, грузин и других народов. Алфавитная нумерация была принята и в древней Руси. Над буквами, обозначавшими числа, ставился специальный знак - титло. Это делалось для того, чтобы отличать их от обычных слов.
Удобны ли алфавитные системы?
Запишем в славянской нумерации число 444:
274
Мы видим, что запись получилась не длиннее нашей. Это объясняется тем, что в алфавитных нумерациях имелось 27 цифр, тогда как в египетской, например, для обозначения всех чисел до 1000 было всего лишь три цифры.
Но алфавитные нумерации имели и крупный недостаток: с их помощью нельзя обозначать сколь угодно большие числа. Они были очень удобны только для записи чисел до 1000.
Правда, славяне, как и греки, умели записывать и большие числа, но для этого к алфавитной системе добавляли новые обозначения. Числа 1000, 2000 и т. д. они записывали теми же буквами, что 1, 2 и т. д., только слева внизу
ставился специальный знак
, например, 1000
обозначали
Аналогично:
Число 10 000 опять обозначалось той же буквой, что и 1, только без титла, но его уже обводили кружком:
Называлось это число «тьмой». Отсюда, между прочим, произошло выражение «тьма народу».
Итак, для обозначения тем первые 9 цифр обводились кружками:
10 тем, или 100 000, было единицей высшего разряда. Ее называли «легион». Для обозначения легионов вокруг первых 9 цифр ставился кружок из точек:
и т. д.
10 легионов составляли новую единицу, которая называлась «леодр». Для обозначения леодров соответствующие числа заключали в кружок из черточек:
Эти обозначения можно рассматривать как зачатки позиционной системы, так как в ней для обозначения единиц разных разрядов применялись одни и те же символы, к которым добавлялись знаки для определения разряда. Такая система называлась «малым числом». В ней обозначения не шли дальше миллионов. Но наряду с этим имелось и «большое», или «великое», число, в котором словом «тьма» обозначался уже миллион. Тьма тем (т. е. 1012) называлась легионом, легион легионов (т. е. 1024) - леодром, леодр леодров (т. е. 1048) - вороном и, наконец, число 1048 называлось колодой. В рукописи XVII в, говорится: «И более сего несть человеческому уму разумевати», т. е. для больших чисел уже нет названий. Для обозначения воронов буквы ставили в кружок из крестиков:
а колоду обозначали так:
Алфавитные нумерации, как мы говорили, были мало пригодны для оперирования с большими числами, встречавшимися уже в древности (например, при астрономических расчетах). В ходе развития человеческого общества эти системы уступили место позиционным. Но остатки алфавитных нумераций сохранились в нашем обиходе и по сей день. Так, мы часто нумеруем пункты при помощи букв алфавита. Правда, буквы служат только для обозначения последовательного порядка, а не количества. Никаких арифметических операций над такими буквами мы уже не производим.
Первой известной нам позиционной системой счисления была шестидесятеричная система вавилонян, возникшая примерно за 2500- 2000 лет до н. э. Основанием ее служило число 60. Следовательно, в ней должно было быть 60 цифр. А таблица умножения должна была состоять из 60·60/2=1800 строк.
Как же вавилоняне записывали свои цифры и как запоминали такую чудовищную таблицу умножения?
Вавилоняне поступали так: записывали все числа от 1 до 59 по десятичной системе, применяя принцип сложения. При этом они пользовались всегда двумя знаками: прямым клином
для обозначения 1 и лежачим клином
для 10. Число 32, например, писали так:
275
Эти знаки и служили цифрами в их системе. Число 60 снова обозначалось тем же знаком,
что и 1, т. е.
Так же обозначались и числа 3600, 60³ и все другие степени 60. Например, число 92 записывали так:
Таким образом, «цифры», т. е. все числа от 1 до 59, вавилоняне записывали по десятичной непозиционной системе, а число в целом - по позиционной системе с основанием 60. Поэтому-то мы и называем их систему шестидесятеричной (а не шестидесятичной, как нужно называть, учитывая только одно основание 60).
Клинописная запись чисел древних вавилонян.
Но нумерация вавилонян имела и еще одну важную особенность: в ней не было знака для
нуля. И если был изображен прямой клин
то без дополнительных пояснений нельзя было определить, какое число записано: 1, 60, 3600 или какая-нибудь другая степень 60. Запись числа 92, приведенная выше, могла обозначать не только 92 = 60 + 32, но и 3600+32=3632.
Она могла также означать 132 /60 или 132 /3600 и т.д.
Таким образом, запись в вавилонской нумерации не носила абсолютного характера - для определения абсолютного значения числа нужны были еще дополнительные сведения. Впоследствии вавилоняне ввели специальный символ для обозначения пропущенного шестидесятичного разряда. Например, число 3632 нужно
было бы записать так:
Но в конце числа этот символ обычно не ставился. Таблицу умножения вавилоняне никогда не запоминали - это было почти невозможно. Они пользовались при своих вычислениях готовыми таблицами умножения, так же как мы теперь пользуемся, например, таблицами логарифмов.
Цифры индейцев племени майя.
Шестидесятеричная система вавилонян сыграла большую роль в развитии математики и астрономии. Следы ее сохранились до наших дней. Так, мы до сих пор делим час на 60 минут, а минуту на 60 секунд. Точно так же, следуя примеру вавилонян, окружность мы делим на 360 частей (градусов).
В начале нашей эры индейцы племени майя, которые жили на полуострове Юкатан в Центральной Америке, пользовались другой позиционной системой - с основанием 20. Свои цифры индейцы майя, как и вавилоняне, записывали, пользуясь принципом сложения. Единицу они обозначали точкой, а пять - горизонтальной чертой (см. рис.), но в этой системе уже был знак для нуля. Он напоминал по своей форме полузакрытый глаз. И, например, число 20 индейцы майя записывали при помощи знака для единицы и внизу знака для нуля (числа писали не в строчку, а столбцами).
Десятичная позиционная система впервые сложилась в Индии не позднее VI в. н. э. Здесь же был введен наш символ для нуля.
Итак, позиционные системы счисления возникли независимо одна от другой в древнем Двуречье, у племени майя и, наконец, в Индии. Все это говорит о том, что возникновение позиционного принципа не было случайностью.
Каковы же были предпосылки для его создания? Что привело людей к этому замечательному открытию?
Чтобы ответить на эти вопросы, мы снова обратимся к истории. В древнем Китае, Индии и в некоторых других странах существовали системы записи, построенные на мультипликативном принципе.
Пусть, например, десятки обозначаются символом X, а сотни - С. Тогда запись числа 323 схематично будет выглядеть так:
ЗС2 X 3.
В таких системах для записи одинакового числа единиц, десятков, сотен или тысяч применяются одни и те же символы, но после каждого символа пишется название соответствую-
276
щего разряда. На аналогичном принципе основаны наши счеты: одно и то же количество косточек означает число десятков, сотен, тысяч и т. д., в зависимости от того, в каком ряду расположены эти косточки.
Но именно такой способ счета применялся при счете «числами-совокупностями». Так, йорубы1, считая раковины-каури (игравшие у них роль денег), раскладывали их в кучки по 20 раковин в каждой, затем 20 таких кучек они объединяли в одну большую кучу и т. д. При таком способе счета подчеркивается то обстоятельство, что с кучами можно поступать так же, как и с отдельными раковинами. Н. Н. Миклухо-Маклай рассказывал о способе счета у папуасов, который уже очень близок к построению чисел по принципу умножения. Чтобы сосчитать число дней до возвращения корвета «Витязь», папуасы поступали следующим образом: «Первый, раскладывая кусочки бумаги на колене, при каждом обрезке повторял «каре-каре» (один), другой повторял слово «каре» и загибал при этом палец прежде на одной, затем на другой руке. Насчитав до десяти и согнув пальцы обеих рук, он опустил оба кулака на колени, повторив «две руки», причем третий папуас загнул один палец руки. Со вторым десятком было сделано то же, причем третий папуас загнул второй палец: то же самое было сделано для третьего десятка».
Рассказывают, что так же считали стада в Южной Африке: один из африканцев считал каждую голову, второй - число десятков, сосчитанных первым, а третий - число десятков, сосчитанных вторым, т. е. число сотен. Если бы мы теперь обозначили палец первого через I, палец второго через X и палец третьего через С, то результат по мультипликативной системе записали бы, например, так: 3C2X3I. В Китае и Индии с древнейших времен существовал именно такой способ записи чисел. Кроме того, индийцы издавна проявляли глубокий интерес к большим числам и способам их записи. В одной из индийских книг - «Лалитавистара» - говорится о состязании между женихами прекрасной Гопы. Предметом состязания были письменность, арифметика, борьба и искусство стрельбы из лука. Почти половина книги посвящена описанию состязаний по арифметике. Победитель Гаутама придумал шкалу чисел, идущих в геометрической прогрессии со знаменателем 100, последним членом которой было 107+9·46 .
Следующей ступенью- к позиционному принципу было опускание названий разрядов при письме (подобно тому, как мы говорим «три двадцать», а не «три рубля двадцать копеек»). Но при записи больших чисел по системе с основанием 10 очень часто бывал необходим символ для обозначения нуля.
Как же появился нуль?
Мы видели, что уже вавилоняне употребляли межразрядовый знак. Начиная со II в. до н. э. греческие ученые познакомились с многовековыми астрономическими наблюдениями вавилонян. Вместе с их вычислительными таблицами они переняли и вавилонскую шестидесятеричную систему счисления, но только числа от 1 до 59 записывали не с помощью клиньев, а в своей, алфавитной нумерации. Но самое замечательное было то, что для обозначения пропущенного шестидесятеричного разряда греческие астрономы начали употреблять символ О (первая буква греческого слова
Этот знак, по-видимому, и был прообразом нашего нуля.
Действительно, индийцы, владевшие уже мультипликативным принципом записи чисел, как раз между II и VI вв. н. э. познакомились с греческой астрономией. Это видно из того, что они переняли и общие теоретические положения этой астрономии, и многие греческие термины.
Одновременно они должны были познакомиться с шестидесятеричной нумерацией и греческим круглым нулем. Индийцы и соединили принципы нумерации греческих астрономов со своей десятичной мультипликативной системой. Это и был завершающий шаг в создании нашей нумерации.
Из Индии новая система распространилась по всему миру. При этом одни народы переняли у индийцев только принцип обозначения чисел, оставив старые начертания цифр, другие заимствовали и написание цифр.
Мы приводим таблицу (см. стр. 278), на которой видно, как постепенно видоизменялись цифры «губар», употреблявшиеся в мавританских государствах, пока они не приняли современной формы.
Откуда произошли сами цифры «губар», до сих пор остается неясным.
В страны Европы новая индийская нумерация была занесена арабами в X-XIII вв. (отсюда и сохранившееся поныне название «арабские цифры»); однако принята она была далеко
¹ Одно из африканских племен.
277
Постепенно изменяясь, цифры «губар» (вторая строка) приняли форму, близкую к современной.
не сразу. Вплоть до XVIII в. в официальных бумагах разрешалось применять только римские цифры. Однако преимущества позиционного принципа счисления были настолько велики, что еще в XIII в. он стал применяться итальянскими купцами. Тогда же Леонардо Пизанский выступил убежденным сторонником новой системы. В Германии, Франции и Англии до конца XV в. новая нумерация почти не употреблялась. Но к концу XVI - началу XVII в. позиционная система одержала решительную победу - ее приняли не только купцы, но и все ученые. Ее стали применять повсеместно.
В России, как мы уже знаем, в старину употреблялась алфавитная система, которая имеет много преимуществ по сравнению с римской. Но и здесь новая нумерация быстро вошла в употребление: во всех без исключения математических рукописях XVII в. применялась десятичная позиционная система счисления. При Петре I индийские цифры уже вытесняют на монетах славянские, а в послепетровские времена славянские цифры вообще быстро исчезают из обихода.
Приведем в заключение слова знаменитого французского математика и физика XVIII-XIX вв. П. Лапласа: «Мысль выражать все числа девятью знаками, придавая им, кроме значения по форме, еще значение по месту, настолько проста, что именно из-за этой простоты трудно понять, насколько она удивительна. Как нелегко было прийти к этому методу, мы видим на примере величайших гениев греческой учености Архимеда и Аполлония, от которых эта мысль осталась скрытой».
ПРОСТЕЙШИЕ НЕОПРЕДЕЛЕННЫЕ УРАВНЕНИЯ
Футбольное поле - это прямоугольная площадка длиной примерно 90 м и шириной 60 м. Как разметить такую площадку? Прямоугольник на листе бумаги строят при помощи линейки и циркуля или линейки и угольника. Эти приборы слишком малы для работы на местности. Они не обеспечат нужной точности в построении прямых углов такой площадки, как футбольное поле. Если же сделать циркуль и угольник достаточно больших размеров, то ими будет невозможно пользоваться.
С давних времен известен очень простой способ построения на местности прямых углов. Выполним такое построение. Возьмем шнур и три колышка. На шнуре отметим 12 равных долей. Затем узлами выделим три части шнура MB, BC, CN так, чтобы первая часть состояла из пяти, вторая из четырех и последняя из трех
Для построения прямоугольной площадки следовало бы взять угольник и циркуль таких размеров.
278
Построение прямого угла на местности.
таких долей. Узлы М и N свяжем вместе и обозначим вновь полученный узел через А.
С помощью колышков натянем часть шнура ВС вдоль данной прямой так, чтобы точка С совпала с точкой, через которую должен быть проведен перпендикуляр к данной прямой. Потом оттянем шнур за узел А так, чтобы участки АВ и АС стали прямолинейными, и вобьем в точке, где будет находиться узел А, колышек. Задача построения на местности прямого угла решена, так как угол АСВ прямой.
Чтобы убедиться в этом, докажем, что прямоугольным будет всякий треугольник, стороны которого, измеренные какой-нибудь единицей измерения, выражаются числами 3, 4 и 5. Для доказательства возьмем прямоугольный треугольник с катетами, равными двум меньшим сторонам данного треугольника, и найдем его гипотенузу х. По теореме Пифагора x² =3² +4². Поэтому х =5. Таким образом, три стороны данного треугольника соответственно равны трем сторонам прямоугольного треугольника. А отсюда следует, что и данный треугольник - прямоугольный.
Доказанное свойство треугольника со сторонами 3, 4 и 5 было, по-видимому, известно еще древнеегипетским землемерам. Поэтому такой треугольник называют египетским. Вся-
кий целочисленный треугольник1, подобный египетскому, также является прямоугольным.
Существуют ли другие целочисленные прямоугольные треугольники.
Если катеты и гипотенузу какого-нибудь целочисленного прямоугольного треугольника обозначить буквами х, у и z, то по теореме Пифагора получим:
z² +y² = z². (1)
Оказывается, что верно и обратное, т. е. если х, у и z - натуральные числа, удовлетворяющие уравнению (1), то треугольник со сторонами х, у и z - прямоугольный.
Целочисленный прямоугольный треугольник для краткости иногда называют пифагоровым.
Наше рассуждение показывает, что задача отыскания всех пифагоровых треугольников сводится к решению уравнения (1) в натуральных числах.
Рассмотрим несколько других задач.
Можно ли 28 Г некоторого вещества отвесить на чашечных весах, имея гири весом только в 3 и 5 Г?
Оказывается, это можно сделать, даже несколькими способами.
Попытаемся найти все способы взвешивания. Для этого поместим груз в 28 Г на правую чашу весов и уравновесим его гирями весом в 3 и 5 Г. Возможны такие случаи: а) все гири находятся на левой чаше весов; б) гири по 3 Г находятся на левой чаше весов, а гири по 5 Г вместе с грузом находятся на правой чаше весов; в) гири по 5 Г находятся на левой чаше весов, а гири по 3 Г вместе с грузом находятся на правой чаше весов.
Если через х обозначить число использованных гирь весом в 3 Г, а через у - число использованных гирь весом в 5 Г, то в соответствии с отмеченными выше случаями получим:
а) Зх+5у=28, (2)
б) Зх =28+5 у, или 3x-5y= 28,
в) 5у=28+3 x, или 5y-3x =28.
Чтобы найти все способы взвешивания, нужно решить каждое из полученных уравнений
¹ Целочисленным называют треугольник, длины сторон которого выражаются целыми числами.
279
в неотрицательных целых числах. Можно решить одно уравнение (2) в целых числах, но при этом нужно иметь в виду, что значения неизвестных х и y указывают не только на число использованных гирь, но и на их место на чашах весов. Так, если значение неизвестного х положительно, то число гирь весом в 3 Г равно х и все они находятся на левой чаше весов; если значение неизвестного х отрицательно, то число гирь весом в 3 Г равно | х | и все они находятся на правой чаше весов.
Сколько нужно взять гирь?
В деревообделочный цех одного завода поступил заказ вырезать из фанеры заготовки двух видов для 1000 изделий. Известно, что на одно изделие идет две заготовки первого вида и три второго. На складе имеется 800 листов фанеры одного образца. Были предложены три способа раскроя этих листов. При первом способе из листа фанеры получается пять заготовок первого вида и две второго, при втором - одна заготовка первого вида и пять второго и, наконец, при третьем - три заготовки первого вида и четыре второго.
Достаточно ли для выполнения заказа листов фанеры, имеющихся на складе? Сколько листов фанеры нужно кроить по первому, сколько по второму и по третьему способам, чтобы выполнить этот заказ?
Обозначим буквами х1, х2, х3 соответственно число листов фанеры, раскроенных по первому, второму и третьему способам. Тогда 5 x1 + x2 +3 х3 - количество полученных заготовок первого вида и 2х1 + 5х2 +4 x3 - количество полученных заготовок второго вида. Так как для выполнения заказа требуется не менее чем 2000
заготовок первого и 3000 заготовок второго вида, то должны выполняться неравенства:
5 х1 +х2 + 3 х3³ 2000,
2 х1 + 5 х2 + 4 x3³ 3000.
Чтобы заменить неравенства строгими равенствами, обозначим через x4 количество заготовок первого вида, которые придется изготовить сверх 2000, а через х5 - количество «лишних» заготовок второго вида. Тогда, учитывая, что х1 + x2 + x3 =800, получим следующую систему уравнений:
Конечно, x4 и x5, так же как и x1, x2, х3, должны быть целыми неотрицательными числами.
Каждому варианту ( х1 , х2, х3) распределения 800 листов фанеры по способам раскроя соответствует решение ( х1, x2, x3 , x4, х5) системы уравнений (3) в целых неотрицательных числах. Наоборот, каждому решению (х1 , х2 , х3, x4, x5) системы (3) в целых неотрицательных числах соответствует определенный вариант распределения 800 листов фанеры по способам раскроя. Поэтому задача о раскрое фанеры приводит к отысканию решений системы (3) в целых неотрицательных числах.
Каждая из рассмотренных задач сводится, как мы убедились, к решению в целых числах некоторых уравнений или систем уравнений. При этом число неизвестных всякий раз превосходило число уравнений. Такие уравнения и системы называют неопределенными. При решении неопределенных уравнений или систем уравнений обычно ищут значения неизвестных, удовлетворяющие тем или иным арифметическим условиям. Например, их решают в целых или рациональных числах.
Еще александрийский математик Диофант (III в. н.э.) занимался решением алгебраических уравнений в рациональных (вообще говоря, дробных) числах. Решением неопределенных урав-
280
Задача о раскрое фанеры - одна из задач бурно развивающейся в настоящее время математической теории, которая называется линейным программированием.
Если во всем искать математику, то можно построить интересную полезную математическую теорию, рассматривая, например, затейливые узоры на древнегреческой вазе или прихотливо повторяющиеся рисунки мозаик и паркета в старинных дворцах. Простейшая математическая теория ряда мозаик получится, если на плоскости рассматривать .мозаики, состоящие из правильных многоугольников. Чтобы особо подчеркнуть важность того, что мозаики получаются повторением рисунка, введем следующее определение. Назовем преобразованием рисунка всякое его перемещение, которое надо совершить, чтобы совместить его с другим таким же рисунком. Оказывается, что для таких преобразований существует очень простая и красивая алгебра и такие преобразования образуют группу (более подробно о такой алгебре и теории групп см. в статье «Чем занимается алгебра?»).
Эти преобразования можем подразделить на несколько видов: параллельный перенос рисунка, поворот его на какой-то угол и зеркальное отражение. При этом оказывается, что на плоскости для любых мозаик из правильных многоугольников может быть только 17 различных групп таких преобразований. Этот замечательный факт установил в 1891 г. знаменитый русский кристаллограф Б. С. Федоров.
Изучение мозаик дает богатую пищу не только для математических исследований, но и для воображения художника. На прилагаемом рисунке можно видеть как «портреты» некоторых абстрактных групп, так и мозаики другого типа. Эти остроумные рисунки сделал датский художник Мориц К. Ешер. Первое впечатление, что утки летят, а всадники скачут только слева направо. Но тут же глаз замечает, что такая же процессия с занимательной точностью движется в противоположном направлении. Художник предлагает каждому попробовать свои силы в составлении таких мозаик. Однако он предупреждает, что такая работа требует усидчивости! Интересно отметить, что для таких произвольных мозаик теория групп уже не является таким же удобным и плодотворным математически» аппаратом, как для правильных мозаик. Но здесь начинается применение другой любопытной математической теории, именно теории о покрытии плоскости без пропусков и наложений фигурами сложных очертаний. И эта математическая теория даёт много интересных и полезных сведений всякому, кто познакомится с ней поближе.
нении в целых числах впервые начали заниматься ученые Индии. Они предложили общий метод для решения в целых числах неопределенных уравнений первой степени с целыми коэффициентами, а также нашли решение в целых числах некоторых неопределенных уравнений второй степени с двумя неизвестными.
Рациональные и целые решения неопределенных уравнений первой степени.
Решить неопределенные уравнения первой степени с целыми или дробными коэффициентами в рациональных числах нетрудно. Возьмем, например, уравнение
29х-13 y =17. (4)
Чтобы найти все решения этого уравнения, узнаем, при каких рациональных значениях одного неизвестного соответствующее значение второго неизвестного рационально. Каждому значению неизвестного х соответствует единственное значение неизвестного у, определяемое из формулы:
29х - 17/13. (5)
Если значение неизвестного х рационально, то и значение неизвестного у, получаемое из формулы (5), рационально.
В формуле (5) роли неизвестных х и у различны. Неизвестному х мы даем произвольное значение, а значение неизвестного у находится в зависимости от выбранного значения неизвестного х. В соответствии с этим называют неизвестное х свободным, а неизвестное у зависимым. Уравнение (4) можно разрешить не только относительно неизвестного у, но и относительно неизвестного х. В таком случае неизвестное у станет свободным, а неизвестное х зависимым.
Для отыскания целых решений уравнения (4) мы не можем непосредственно воспользоваться формулой (5), так как при целых значениях одного неизвестного второе неизвестное не обязательно принимает целые значения. Чтобы найти все целые решения уравнения (4), найдем такие целые значения неизвестного x, для которых соответствующее значение неизвестного у является целым числом.
Это незначительное на первый взгляд изменение постановки задачи открывает путь для ее решения.
Замечая, что
29/13 =2+3/13, а 17/13=1+4/13,
и пользуясь формулой (5), получим:
у =2х-1+(3 x-4)/13. (6)
Мы должны узнать, при каких целых значениях неизвестного х неизвестное у принимает целые значения. Так как при целом х число 2х- 1 является целым, то из формулы (6) следует, что неизвестное у при целом х только в том случае принимает целое значение, если выражение (3 x-4)/13 есть целое число.
Наша задача еще не решена, но мы приблизились к цели.
В самом деле, полагая (3 x-4)/13 = у1, замечаем, что вопрос, при каких целых значениях неизвестного х неизвестное у принимает целые значения, равносилен вопросу о целых решениях уравнения
З x -13 y1 =4. (7)
Таким образом, решение в целых числах уравнения (4) удалось свести к решению в целых числах уравнения (7). Чем же второе уравнение предпочтительнее первого?
Самым простым из неопределенных уравнений первой степени естественно считать такое, у которого хотя бы один из коэффициентов при неизвестных равен 1 или -1. В этом случае неизвестное с таким коэффициентом при любых целых значениях остальных неизвестных при-
281
Будем решать задачу методом рассеивания.
нимает целые значения. Поэтому чем меньше наименьшая из абсолютных величин коэффициентов при неизвестных, тем уравнение предпочтительнее. В уравнении (4) наименьшая из абсолютных величин коэффициентов при неизвестных равна 13, а в уравнении (7) равна 3. Как удалось достичь этого? Коэффициент при неизвестном х и свободный член уравнения были заменены остатками от деления этих чисел на 13. Но остаток от деления целого числа на натуральное число всегда меньше этого натурального числа. Понятно, почему с самого начала неизвестное у было выражено через неизвестное х: мы выбрали неизвестное с наименьшим по абсолютной величине коэффициентом. Теперь ясно, как поступать с уравнением (7).
При каких целых значениях неизвестного y1 неизвестное х принимает целые значения?
Из равенства:
x=( 4+13 y1)/3=1+4y1 +(1+y1)/3 (8)
находим, что неизвестное х при целых значениях неизвестного у1 только в том случае принимает
целые значения, если (1+y1)/3 есть целое число.
Обозначая через х1 это выражение, получим 1+y1 =3x1, или
3 x1 -y1 =1. (9)
Таким образом, задача сведена к решению в целых числах уравнения (9). Но решить в целых числах уравнение (9) - значит узнать, при каких целых значениях неизвестного x1 неизвестное y1 принимает целые значения. Но y1 = 3 x1 -1, поэтому у1 принимает целые значения при любых целых значениях неизвестного X]. Из равенств (8) и (6) последовательно найдем выражения для неизвестных x и y .
х =1+4 (3x1 - 1)+ х1 =13 х1 - 3, у= 2(13 x1 - 3)-1 +3х1 - 1=29 x1 -8.
Из приведенных рассуждений следует, что формулы:
при x1 =0,+: 1,+2,+3,... дают все целые решения уравнения (4).
Аналогично решается уравнение с тремя и более неизвестными. Показанный на примере метод решения неопределенных уравнений в целых числах несущественно отличается от метода, предложенного индийцами. В связи с тем что при решении неопределенного уравнения по этому методу оно сводится к цепи уравнений с уменьшающимися коэффициентами, индийские математики назвали этот метод методом рассеивания.
Итак, нам нужно решить в целых числах уравнение (2). Определяем неизвестное х:
x =(28-5 y)/3=9- y +(1-2 y)/3 Верно и такое равенство:
х =9-2 у+( 1 + y) /3 .
Им-то мы и воспользуемся. Ведь наша цель - уменьшить коэффициент при неизвестном. Введем обозначение: x1 = (1 +y)/3. Задача сведена к решению в целых числах уравнения 3x1 - y =1. Решая это уравнение, получим y =3 х1 -1, где х1 - любое целое число. А тогда
х= 9-2·(3 x1 -1)+ x1 = 11-5 х1. Таким образом, общее решение уравнения (2) можно записать так:
282
Найдем несколько решений этого уравнения:
Уравнение (2) имеет бесконечное множество решений, но мы сможем воспользоваться только некоторыми. Это зависит от числа гирь в нашем распоряжении, да и размеров чаш.
Мы рассмотрели два уравнения первой степени. Каждое из них, как удалось установить, имеет целочисленные решения. Однако на-
Задача о взвешивании решена!
ряду с ними можно указать уравнения, которые решений в целых числах не имеют. Таково, например, уравнение
З х -6 у =5. (11)
В самом деле, допустив, что при некоторых целых х и у равенство (11) верно, мы получим, что 5 делится на 3.
Какие неопределенные уравнения разрешимы в целых числах?
Можно ли для всякого разрешимого в целых числах неопределенного уравнения первой степени найти его решение методом рассеивания?
На первый вопрос отвечает теорема:
Уравнение с целыми коэффициентами а1,
а2 , ...,аn, b :
а1 х1 + а2 x2 +...+ аn xn = b (12)
разрешимо в целых числах только в том случае, если свободный член b делится на наибольший общий делитель чисел а1, а2, ..., аn .
Ответим на другой вопрос: всегда ли предложенный метод решения в целых числах неопределенных уравнений первой степени приводит к цели?
Если а1 - наименьший по абсолютной величине коэффициент при неизвестном в уравнении (12), то мы заменяем это уравнение другим, в котором все коэффициенты, кроме коэффициента a1, заменены остатками от деления этих чисел на а1. Если хотя бы один из коэффициентов а2, а3, ..., аn не делится на а1, то получим уравнение, коэффициенты которого по абсолютной величине меньше, чем у данного. С этим уравнением поступаем так же, как сданным. Если все числа а2, а3, ..., аn делятся на a1 а b не делится, то данное уравнение неразрешимо. Если все числа a2, а3, ..., аn и b делятся на а1, то, деля обе части уравнения на а1, получим уравнение, целые решения которого находятся без труда.
Из этого рассуждения следует, что описанный метод позволяет найти целые решения всякого разрешимого в целых числах неопределенного уравнения с целыми коэффициентами.
При решении в рациональных числах неопределенных систем уравнений первой степени с рациональными коэффициентами обычно пользуются методом последовательного исключения неизвестных. Решим, например, в рациональных числах такую систему уравнений:
Из первого уравнения находим:
Подставляя значение неизвестного х во второе уравнение, получим:
Давая в уравнении (14) неизвестному z какое-нибудь рациональное значение, т. е. принимая неизвестное z за свободное неизвестное, а за зависимые неизвестные х и у, мы, пользуясь равенствами (14) и (13), сможем найти все решения в рациональных числах данной системы уравнений.
283
В целых числах такую систему можно решить сходным способом. Сначала рассматривают одно из уравнений системы и решают его в целых числах. Найденные выражения для неизвестных этого уравнения через некоторые вспомогательные целочисленные неизвестные подставляют во второе уравнение. Решив в целых числах полученное уравнение с новыми неизвестными, можно найти все решения в целых числах и данной системы уравнений.
284
Теперь приступим к решению системы уравнений (3). Мы имеем три уравнения с пятью неизвестными. Поэтому два неизвестных будут свободными, а остальные три - зависимыми. Конечно, в качестве зависимых неизвестных нужно брать те, у которых абсолютная величина коэффициентов минимальна.
Поэтому выберем в качестве свободных неизвестных х1 и х2 и выразим x3, х4 , х5 через x1 и x2. Для этого значение х3 = 800- х1 - x2 подставим в первые два уравнения, получим:
x3 =800- х1 -х2 , х4 =400 + 2 х1 -2 х2, х5 = 200- 2 x1 + х2 .
Теперь, давая x1 и x2 целые значения, получим всевозможные решения системы (3) в целых числах.
Исследуйте самостоятельно, какие целые неотрицательные значения следует давать х1 и х2, чтобы х3, х4 и х5 также были неотрицательными.
Ниже приведена таблица некоторых решений системы (3).
Из таблицы видно, что листов фанеры достаточно и что самый выгодный способ раскроя будет при x1 =0, x2 =100, х3 =700. В этом случае
образуются «лишние» заготовки еще для 100 изделий. В других случаях «лишние» заготовки будут некомплектными. Но нужно ли раскраивать все 800 листов? Ведь нужны заготовки для 1000 изделий, а не для 1100.
Поэтому практический интерес представляет следующий дополнительный вопрос к этой задаче: какое наименьшее число / листов фанеры следует взять со склада и какими из указанных способов следует кроить взятые листы, чтобы выполнить заказ? Для ответа на этот вопрос из всех решений в целых неотрицательных числах системы уравнений
для которого f = x1 + x2 + x3 принимает наименьшее значение, или, как мы будем говорить дальше, удовлетворяет условию минимальности.
Чтобы облегчить поиски, откажемся временно от требования, чтобы значения неизвестных были целыми. Попытаемся решить нашу задачу удачным выбором свободных неизвестных. Удобнее всего такими выбрать x4, х5 и какое-нибудь из неизвестных x1 , x2, x3. Поэтому, исключая из уравнений (15) сначала, например, x1, а затем x2 и опуская промежуточные выкладки, будем иметь:
При данном значении х3 наименьшее значение f мы получим, если неизвестным x4 и х5 дадим нулевое значение (это и понятно, ведь x4 и x5 - количество «лишних» заготовок!). Пусть x4 = x5 =0. Легко видеть, что при возрастании значений неизвестного х3 значение f будет убывать. Но рост х3 сдерживается требованием, чтобы значения неизвестных х1 и x2
были неотрицательными. Так как 7000/11<11000/44,
то из равенств [см. (16) при x4 = x5 =0]:
видно, что при возрастании х3 отрицательные значения прежде всего будет принимать неиз-
284
вестное x1. Поэтому естественно неизвестное x1 сделать свободным, а неизвестное х3 - зависимым.
Исключая из уравнений (15) неизвестные x2 и x3, найдем:
x2 =(1/11)(1000+14 x1 - 4 x4 +3 x5),
x3 =(1/11)(7000-23 x1 +5 x4 - x5) , f =(1/11)(8000+2 x1 + x4 +2 x5).
Легко видеть, что наименьшее значение f получим, если свободным неизвестным х1 , x4 и x5 дадим нулевые значения. При этом для зависимых неизвестных получим положительные значения:
х2 = 1000/11 , x3 = 7000/11.
Следовательно, решение
х1 = 0; x2 =1000/11=90,9...;
х3 = 7000/11 = 636,3 ...; x4 =0; х5 =0
системы (15) удовлетворяет условию минимальности. Но нам требуется найти целочисленное решение в неотрицательных числах, удовлетворяющее условию минимальности. Из приведенных рассуждений следует, что для такого решения f³ 8000/11 = 727,2... или даже f³ 728,
так как число должно быть целым. Можно ожидать, что искомое решение мы получим, если немного изменим значение неизвестных. Положим, например, х1 =0, х2 = 91, х3 = 637. Тогда:
f = x1 + x2 + x3 =728,
5·0+91+3·637=2002>2000,
2·0+5·91+4 ·637=3003>3000.
А это убеждает нас, что целочисленное решение с условием минимальности найдено. Итак, со склада достаточно взять лишь 728 листов фанеры и 91 из них кроить по второму, а остальные по третьему способу.
Решенная нами задача о раскрое фанеры относится к числу задач, составляющих предмет теории линейного программирования. В этой теории рассматривают задачи следующего типа: из всех решений в неотрицательных числах некоторой системы уравнений первой степени найти решение, удовлетворяющее условию минимальности. Иногда, как в задаче о раскрое фанеры, выдвигают дополнительное требование, чтобы значения неизвестных были целыми числами.
Жозеф Луи Лагранж.
Весьма многие проблемы экономики страны, в частности вопросы планирования производства и перевозок, приводят к этим задачам.
Решение в целых числах неопределенных уравнений степени выше первой с целыми коэффициентами - во многих случаях задача более сложная, чем решение в целых числах неопределенных уравнений первой степени.
Индийские математики (V - XII вв.) нашли решение в целых числах некоторых уравнений второй степени с двумя неизвестными. Полностью задачу нахождения в целых числах неопределенных уравнений второй степени с двумя неизвестными решил в 1766 г. французский математик Ж. Лагранж.
Уравнения третьей степени с двумя неизвестными до сих пор до конца не исследованы. С некоторыми типами таких уравнений удалось справиться советскому математику Б. Н. Делоне. Нужно сказать, что даже установить число решений таких уравнений третьей и более высоких степеней исключительно трудно.
285
В начале нашего столетия норвежскому математику А. Туэ удалось доказать интересную теорему:
Неопределенное уравнение с целыми коэффициентами:
а0 хn +а1 х n-1 у + а2 хn-2 у² ...аn уn = b ,
где n - целое число, большее двух, имеет только конечное множество решений (в частности, может не иметь решений) в целых числах, за исключением случаев, когда левая часть этого уравнения есть степень однородного двучлена первой степени или трехчлена второй степени.
Еще более трудным является вопрос о решении в целых числах неопределенных уравнений выше первой степени с тремя и более неизвестными. До сих пор неизвестен общий метод решения таких уравнений. Уравнение (1) является простейшим из них. Древние греки и даже вавилоняне знали тождество:
(2 mn)² +( m² - n²)² = ( m² + n²)² .
Пользуясь таким тождеством, нетрудно находить натуральные решения уравнения (1). Для этой цели нужно в формулах
переменным m и n давать натуральные значения с условием, что m > n. При помощи простых соображений доказывается, что из формул (17) можно получить все решения уравнения (1) в натуральных и взаимно простых числах, если параметрам m и n давать натуральные, взаимно простые и разной четности значения с условием m > n .
Занимаясь неопределенными уравнениями, известный французский математик П. Ферма высказал в середине XVII в. предположение, что для любого натурального числа n , большего 2, уравнение
хn + уn = zn
не имеет решений в натуральных числах. Доказательство этого утверждения для n =3 и n =4 было найдено Л, Эйлером.
В дальнейшем предпринимались многочисленные попытки доказать это утверждение (так
называемую великую теорему Ферма) полностью, но они не имели успеха1. Однако такие попытки не были безрезультатными - они содействовали возникновению и развитию нового отдела математики - алгебраической теории чисел.
В 1770 г. шотландский математик Э. Варинг высказал предположение, что для всякого натурального k, не равного 1, существует такое натуральное число r , что при любом натуральном /V, уравнение
хk 1 +хk 2 ... + xkr = N (18)
разрешимо в целых числах. Доказательство частного случая этого утверждения принадлежит Ж. Лагранжу. Он установил, что всякое число можно представить в виде суммы четырех квадратов целых неотрицательных чисел, например:
23= 3² +3² + 2² +1², 26=4² +3² +1² +0² .
Полностью эту теорему удалось доказать в 1909 г. немецкому математику Д. Гильберту. Но ему не удалось дать оценку минимального числа r , для которого уравнение (18) разрешимо в целых неотрицательных числах. Значительный успех в определении g(k) (так обозначают наименьшее r , для которого при любом натуральном N уравнение (18) разрешимо в целых неотрицательных числах) стал возможен только после создания советским математиком И. М. Виноградовым особого метода для решения этой и сходных с ней задач.
Сравнительно недавно стали изучаться показательные неопределенные уравнения. К этой области принадлежит интересная теорема советского математика А. О. Гельфонда:
Уравнение ах + bу = cz, где а, b и с - целые, каждое из которых не равно ни нулю, ни степени двойки, может иметь не более чем конечное число решений в целых числах х, у и z.
Наиболее трудными являются неопределенные уравнения, связанные каким-либо способом с простыми числами. Но и в этой области за последние годы наметился успех. Мы не будем останавливаться здесь на этой сложной и увлекательной проблеме.
¹ В настоящее время теорема доказана для всех n £ 10 000.
Кое-кто, возможно, считает, что различные замысловатые линии и поверхности можно встретить только в книгах ученых-математиков.
Однако стоит внимательно осмотреться, и мы сразу обнаружим вокруг нас всевозможные геометрические фигуры. Оказывается, их очень иного. Просто мы их раньше не замечали,
Вот комната. Все ее стены, пол и потолок
являются плоскостями (не будем обращать внимания на проемы окон и дверей), а сама комната имеет форму параллелепипеда.
Посмотрим на паркетный пол. Планки паркета - прямоугольники или квадраты. Пройдем в ванную комнату. Плитки пола там часто бывают правильными шестиугольниками или восьмиугольниками, между которыми уложены небольшие квадратики.
287
Но вернемся в комнату и посмотрим на мебель. Шкаф в своей основе - параллелепипед. Письменный стол не что иное, как очень плоский параллелепипед, лежащий на двух других параллелепипедах - тумбочках, в которых размещаются ящики. На столике - лампа с абажуром. Этот абажур - конус.
Ведро представляет собой усеченный конус, у которого верхнее основание больше нижнего. Впрочем, ведро бывает и цилиндрической формы. Вообще цилиндров и конусов в доме очень много. Все прямые трубы (водопровод, паровое отопление, газопровод) - цилиндры. А там, где трубы изогнуты, образуются так называемые каналовые или трубчатые поверхности.
В буфете стоит посуда. Вот граненый стакан с боковой поверхностью правильной многогранной усеченной пирамиды. Чайное блюдечко - тоже усеченный конус. Воронка состоит из двух усеченных конусов, которые переходят один в другой.
Нальем в стакан воду. Края ее поверхности имеют форму круга. Наклоним стакан так, чтобы вода не выливалась; тогда край водной поверхности станет эллипсом.
Выйдем на улицу. Перед нами - дома. Если не обращать внимания на различные особенности их архитектурной отделки, можно сказать, что стены домов являются плоскостями. Две стены, встречаясь под углом, пересекаются по прямой линии. Дом в целом, с этой точки зрения, есть тело, ограниченное пересекающимися друг с другом плоскостями, т. е. многогранник. На вклейке изображен такой дом-многогранник. Он состоит из нескольких параллелепипедов и призм, переходящих друг в друга.
Многие жилые дома, дворцы, общественные здания украшены колоннами. Колонны в большинстве случаев - цилиндры, но могут иметь и более сложную форму.
Кто был в Москве, знает, как красив Московский Кремль. Прекрасны его башни! Сколько интересных геометрических фигур положено в их основу! Вот, например, Набатная башня (см. рис. между стр. 288-289). На высоком параллелепипеде стоит параллелепипед поменьше, с проемами для окон, а еще выше воздвигнута четырехугольная усеченная пирамида. На ней расположены четыре арки, увенчанные восьмиугольной пирамидой.
По улице движутся автомобили, трамваи, троллейбусы. Их колеса с геометрической точки зрения - круги. Мы настолько привыкли к
288
Каких только геометрических форм не встретишь вокруг! Форму различных многогранников имеют кристаллы, причудливую симметричную форму - листья, а шары - главная деталь шарикоподшипника. Форму тора имеет спасательный круг, а планета, на которой мы живем, - форму геоида.
Многим условиям должны удовлетворять геометрические формы различных сооружений, создаваемых человеком. Обтекаемую форму придают пароходу, -подводной лодке, автомобилю (особенно гоночному). А космическая ракета - транспортное средство будущего - имеет форму конуса, поставленного на цилиндр. Самую разнообразную форму имеют здания и их различные детали.
этому, что даже не думаем об окружности как о кривой, которая помогла людям во много раз облегчить труд. А ведь было время, когда люди еще не знали колеса.
Посмотрим на автомобильные фары. Их внутренняя поверхность зеркальная. Конструкторы автомобилей знают, что свет должен выходить из фар пучком параллельных лучей: тогда сила света будет слабее всего уменьшаться с увеличением расстояния. А чтобы зеркало фар отражало лучи параллельным пучком, зеркалу нужно придать форму параболоида вращения, внутри которого в определенной точке (в фокусе) находится лампочка. Параболоид вращения - это поверхность, которая образуется при вращении параболы вокруг ее оси.
У некоторых марок автомобилей фары находятся внутри капота и снаружи виднеется только стекло. У других же весь корпус фары выступает наружу и ясно видно, что она параболической формы.
Параболоид вращения служит отражающим зеркалом и у прожекторов, которые посылают в небо мощные лучи. Форму параболоида вращения имеет купол Московского планетария (см. рис. на вклейке).
Перед нами мост. Арки мостов бывают разной формы: одни из них эллиптические, другие- параболические. На парапете моста часто укрепляют спасательные круги. Они по форме очень близки к тору. Тор - это поверхность, образующаяся при вращении окружности вокруг оси, когда ось не пересекается с окружностью, но лежит с ней в одной плоскости (см. рис. на вклейке).
Мы подходим к радиостанции. Здесь возвышаются радиомачты с излучателями электромагнитных колебаний на верхушках. Но какой странной формы эти мачты! Они состоят из отдельных частей (секций), поставленных друг на друга. А каждая секция похожа на круглую сетку, образованную прямолинейными стержнями.
289
Рассмотрим любую из секций (они отличаются только размерами). Представим себе, что стержни расположены вплотную друг к другу. В таком случае они будут образовывать замечательную кривую поверхность, которая называется одно полостным гиперболоидом. Те прямолинейные стержни, которые мы видим, не что иное, как прямолинейные образующие этой поверхности. Посмотрите на однополостный гиперболоид (рис. на стр. 292-293). Трудно поверить, что он состоит из прямых линий. Однако это именно так. Эта конструкция очень легка и отличается исключительной прочностью.
Иногда строят односекционные вышки из прямолинейных металлических стержней высотой в многоэтажный дом. Так построена водонапорная башня около Сельскохозяйственной академии им. К. А. Тимирязева в Москве. Такие башни были впервые сконструированы советским инженером В. Г. Шуховым и называются шуховскими.
Своим названием однополостный гиперболоид обязан гиперболе. Эта поверхность образована вращением гиперболы вокруг той из ее осей, которая ее не пересекает. В таком случае при вращении образуется единая поверхность (одна полость).
А теперь сядем в поезд. Город остался далеко позади. Бегут телеграфные столбы. Но и здесь геометрия не покидает нас. Вдоль дороги на столбах натянуты провода. Вот проходит линия высоковольтной передачи. Провода от собственной тяжести слегка провисают. Какая же линия образуется при этом? Такой вопрос имеет большое практическое значение. Когда требуется определить длину провода, необходимого для передачи электроэнергии на большие расстояния, приходится учитывать, что его длина (благодаря провисанию) будет большей, чем расстоя-
Возьмем какое-нибудь целое положительное число, например 13. Прибавим сумму его цифр, тогда образуется число 17. К этому результату тоже прибавим сумму его цифр, образуется число 25. Продолжая так действовать, получим последовательность чисел: 13, 17, 25, 32, 37, 47, ...
Прежде всего давайте выясним, можно ли полученную последовательность продолжить влево, т. е. существует ли число, которое в сумме с его же цифрами дало бы 13? Пробуем 12:
12+3=15 - плохо. Пробуем 11:
11+2=13 - хорошо. Значит, перед числом 13 в нашей последовательности должно быть число 11. А перед ним? Попробуем 10:
10 + 1 = 11 - хорошо. А перед числом 10? Здесь и без пробы ясно, что числу 10 будет предшествовать 5. В самом деле:
5 + 5 = 10.
Но уже для числа 5 нет предшественника среди целых положительных чисел. Таким образом, в последовательности:
5, 10, 11, 13, 17, 25, ... все числа, кроме пятерки, «сформированы» по единому правилу, а число 5 оказалось как бы «самородком».
Отправимся в поиски других «самородков», аналогичных числу 5.
Однозначные «самородки» обнаруживаются сразу. Это, очевидно, 1, 3, 5, 7 и 9.
Из двузначных наименьшим «самородком» будет число 20. (Легко убедиться, что ни одно из чисел от 1 до 19 в сумме с его же цифрами не образует 20.) Следующий двузначный «самородок» - число 31. (Убедитесь!)
А сколько же всего двузначных «самородков»? Выясните самостоятельно. (Ответ на стр. 321.)
Есть «самородки» и среди многозначных чисел, например: 132, 143, 233, 929, 1952, 874 531 и т. д.
Не так-то легко было выявить их!
290
ние между конечными пунктами линии электропередачи. И чтобы точно подсчитать длину проводов, необходимо определить, какая именно линия образуется при провисании провода между двумя столбами. Оказывается, что между каждыми двумя столбами провод провисает по так называемой цепной линии. Точно так же провисает и шнур, укрепленный на двух гвоздиках, вбитых в стену. Цепная линия очень похожа на параболу, но это не парабола; свойства цепной линии и параболы различны.
Наш поезд идет по прямолинейному железнодорожному пути и время от времени плавно проходит закругления рельсов. Плавное движение поезда на изгибах железнодорожного полотна обусловлено тем, что железнодорожный путь на закруглениях искривлен не просто по окружности, а также по некоторым довольно замысловатым кривым. Лишь иногда, на очень крутых поворотах, мы ощущаем, что нас слегка отталкивает к одной из стенок вагона. Мы знаем, что на закруглениях на вагоны действует сила, которую называют центробежной. Она стремится опрокинуть вагоны и отклоняет все тела, находящиеся в поезде, к внешней стороне закругления.
Чтобы вагоны не опрокинулись, внешний рельс железнодорожного полотна на повороте слегка поднимают по сравнению с внутренним, и этот подъем тем больше, чем круче поворот. Но если заставить поезд сразу переходить с прямолинейного участка пути на круговой, то надо сразу и круто приподнять один из рельсов и вагоны будут испытывать при переходе резкие и сильные толчки. Чтобы этого избежать, переход на закругление делают постепенным. После прямолинейного участка пути рельсы сначала укладывают по так называемой переходной кривой (вдоль которой искривленность возрастает постепенно) и лишь потом эту кривую переводят в дугу окружности. Так поступают и в конце поворота. В качестве переходных используются разные линии (в зависимости от кривизны поворота, скорости поезда на повороте и т. д.). Обычно применяют либо дугу кубической параболы, либо дугу лемнискаты, либо дугу спирали Корню (рис. на стр. 292-293).
До сих пор мы говорили только о тех простейших линиях и поверхностях, которые видны с первого взгляда. А если присмотреться внимательнее, то обнаружим все новые и новые линии и поверхности.
Заглянем на завод. Заводские трубы - пример усеченного конуса: широкие снизу, они постепенно суживаются кверху. На заводе работают станки. Какое множество самых разнообразных линий описывают различные движущиеся части станков! На любом винте имеются винтовые нарезки. Мы увидим станки с эллиптическими колесами, зубчатые колеса с самыми разнообразными формами зубцов, выточенных по дуге циклоиды, эллипса, эвольвенты круга. Свойства этих кривых, имеющих важное применение в технике, изучаются средствами высшей математики.
Кажется, мы не упомянули еще о шаровой поверхности. А ведь она встречается часто. Вспомним хотя бы шариковые подшипники. Более того, форму шара придают иногда и газгольдерам, т. е. резервуарам для хранения газа (см. рис. на стр. 292-293). Это объясняется одним замечательным свойством шаровой поверхности: на изготовление шара расходуется значительно меньше материала, чем на сосуд любой другой формы того же объема.
А сколько еще встречается различных поверхностей, сложных по форме, не имеющих специальных названий!
Вот паровой котел, напоминающий цилиндр. В нем находится пар под высоким давлением. Поэтому стенки цилиндра слегка (пусть незаметно для глаза) изгибаются, образуя поверхность очень сложной и неправильной формы, которую, однако, инженеры обязаны хорошо знать, чтобы суметь рассчитать котел на прочность. Сложную форму имеет и корпус подводной лодки. Он должен быть хорошо обтекаемым, прочным и вместительным. От формы кора-
С помощью кусочков пластилина я соорудил пирамиду и заметил, что в этой конструкции содержится четыре равных равносторонних треугольника.
«А не могу ли я теперь образовать в одной плоскости четыре равных равносторонних треугольника из шести одинаковых отрезков?»
Прикинул на спичках - получилось! И пластилин не потребовался.
Если вам не удастся самостоятельно воспроизвести эту новую конструкцию, взгляните на страницу 321.
291
бельного корпуса зависит и прочность корабля, него устойчивость, и скорость.
Высокие скорости движения заставили инженеров обратить серьезное внимание на форму современных поездов, самолетов, автомобилей. Именно от нее зависит встречное сопротивление воздуха, которое быстро возрастает с увеличением скорости. А если форма будет удачной, обтекаемой, сопротивление воздуха можно значительно уменьшить. Например гоночный автомобиль; его кузову придают такую форму, чтобы встречные потоки воздуха плавно обтекали машину и плотнее прижимали ее к земле (см. рис. на стр. 288-289).
Мотор автомобиля заключен в обтекаемый капот, ветровое стекло отклонено назад, крыша кузова плавно переходит в наклонную заднюю стенку, И капот, и крыша, и задняя стенка не плоские. Они представляют собой сложные поверхности, с которыми школьная математика не имеет дела. Но ими очень интересуются инженеры, которые тщательно их рассчитывают в своих конструкторских бюро.
Мы живем в эпоху завоевания космоса. Наши ракеты запускают космические корабли, спутники Земли. Космическая лаборатория сфотографировала обратную сторону Луны.
Какие геометрические формы мы здесь используем? В основе корпус ракеты состоит из цилиндра, заключающего внутри себя двигатели и горючее. В конической головной части помещается кабина с приборами или с космонавтом (см. рис. на стр. 288-289).
Итак, мы познакомились со множеством различных линий, поверхностей и тел, которые нас окружают. Теперь вы и сами, несомненно, заметите множество геометрических форм, о которых мы здесь не упоминали.
Впрочем, об одной из них, о линии, которую никто не видит, но которая всегда находится около нас, мы расскажем, ибо заметить ее самому, ничего не зная о ней заранее, невозможно.
Пол и потолок в нашей комнате поддерживаются балками, концы которых вмурованы в стены. Балки под влиянием большой нагрузки слегка прогибаются (этот прогиб незаметен для глаза), и, чтобы рассчитать допустимую нагрузку на балки, архитектор должен знать линию ее прогиба. Оказывается, балка, поддерживающая пол или потолок, прогибается по кривой, которая называется параболой 4-й степени. Не будет преувеличением сказать, что эта линия всегда находится у нас под ногами и всегда висит над нашей головой.
Мы видим, сколько самых разнообразных
геометрических линии и поверхностей использует человек в своей деятельности - при строительстве жилищ, фабрик, заводов, мостов, машин, в транспорте. Пользуется же он ими не из простой любви к интересным геометрическим фигурам, а потому, что свойства этих геометрических линий и поверхностей позволяют с наибольшей простотой решать разнообразные технические задачи.
Но чтобы применять эти свойства в технике, надо их знать. Следовательно, надо изучать все эти линии и поверхности. И не только их, но и многие другие, так как техника развивается и с каждым годом использует для своих нужд все новые и новые геометрические формы. Изучая свойства разных линий и поверхностей, мы ставим себе целью выразить эти свойства в виде формул, чтобы уметь по ним производить расчеты машин, зданий и других сооружений.
До сих пор мы в основном упоминали о геометрических формах, созданных руками человека. Однако и в самой природе очень много замечательных геометрических форм.
Так, мы живем на своеобразной поверхности, которая хотя и именуется земным шаром, но на самом деле является, как говорят астрономы, геоидом и по форме очень близка к эллипсоиду вращения (рис. на стр.288- 289). Этот эллипсоид образован вращением эллипса вокруг его малой оси. Правда, он мало отличается от шара (полуоси эллипса, вращением которого образован эллипсоид, относятся
друг к другу как 299/300). Но все-таки это различие приходится принимать во внимание при составлении географических карт.
Взглянем на кристаллы (рис. на стр. 424- 425). Мы обнаружим в них сочетание призм, пирамид и других многогранников.
Листья на деревьях ограничены самыми причудливыми линиями.
Ничего не может быть проще и однообразнее для глаза, чем безграничная плоская поверхность моря в безветренную погоду. Но сколько хлопот причиняет людям морская поверхность, едва подует ветер! Вначале образуются неболь-
292
Форму разнообразных геометрических фигур имеют все архитектурные и строительные конструкции.
1. Радиомачта, каждая секция которой представляет собой однополостный гиперболоид.
2. Мост с параболической (слева) и эллиптической арками.
3. Газгольдеры шарообразной формы.
4. Заводские трубы - усеченные конусы.
5. Поезд делает поворот по переходной кривой:
а) схема переходной кривой,
б) переходная кривая - спираль Корню,
в) переходная кривая - лемниската Бернулли,
г) переходная кривая - кубическая парабола.
Полуправильные выпуклые многогранники. Их грани - правильные многоугольники разных наименований, а все многогранные углы равны между собой.
Всего существует тринадцать вполне определенных полуправильных многогранников (они были известны Архимеду, поэтому их также называют телами Архимеда) и еще две бесконечные серии так называемых призм и антипризм Архимеда.
На рисунке изображены все тринадцать типов полуправильных многогранников: 1) усеченный тетраэдр (грани - правильные треугольники и шестиугольники), 2) кубооктаэдр (грани - правильные треугольники и квадраты), 3) усеченный октаэдр (грани - квадраты и правильные шестиугольники), 4) усеченный куб (грани - правильные треугольники и восьмиугольники), 5) икосододекаэдр (грани - правильные треугольники и пятиугольники), 6) усеченный икосаэдр (грани - правильные пятиугольники и шестиугольники) 7) ромбокубоэктаэдр (грани - правильные треугольники и квадраты), 8) плосконосый куб (грани - правильные треугольники и квадраты), 9) усеченный додекаэдр (грани - правильные треугольники и десятиугольники), 10) ромбоикосододекаэдр (грани - правильные треугольники, пятиугольники и квадраты), 11) усеченный кубооктаэдр (грани - квадраты, правильные шестиугольники и восьмиугольники), 12) плосконосый додекаэдр (грани - правильные треугольники и пятиугольники), 13) усеченный икосододекаэдр (грани - квадраты, правильные шестиугольники и десятиугольники).
На всех чертежах показаны также правильные многогранники, из которых усечением получаются полуправильные.
Подсчитайте, сколько каких граней имеет каждое из тел Архимеда, сколько вершин, сколько ребер. Правильность этого подсчета можно проверить по формуле Эйлера, верной для всякого выпуклого многогранника
Г + В − Р = 2,
где Г - количество граней, В - количество вершин, Р - количество ребер.
шие волны, потом они принимают самую причудливую геометрическую форму, сталкиваясь между собой, обгоняя друг друга, попадая в узкие проливы или на отмели, ударяясь о стенки молов и причалов. Формы поверхности этих волн приходится изучать в физике и механике, так как на основе этого изучения проектируются корпуса кораблей, наименее подверженные качке, а также наиболее прочные стенки волнорезов и набережных, успешно сопротивляющиеся ударам волн.
Во многих случаях наблюдения над явлениями природы помогают человеку в решении его технических задач. Достаточно сказать, что на заре развития авиации наш знаменитый ученый Н. Е. Жуковский, которого В. И. Ленин назвал «отцом русской авиации», и С. А. Чаплыгин исследовали полет птиц, чтобы сделать выводы относительно наивыгоднейшей формы крыла самолета и условий его полета.
Из всего сказанного видно, какую важную роль в нашей жизни играет геометрия.
Наша школьная, элементарная геометрия изучает лишь простейшие из геометрических фигур. Но существуют и другие геометрические науки, изучающие более сложные линии и поверхности.
Истоки геометрии, как и других наук, лежат в практической деятельности людей. Само слово «геометрия» - греческое, в переводе означает «землемерие».
Люди очень рано столкнулись с необходимостью измерять земельные участки. Уже за 3-4 тыс. лет до н. э. каждый клочок плодородной земли в долинах Нила, Тигра и Евфрата имел значение для жизни людей. После разлива рек, особенно Нила, приходилось вновь делить землю. Это требовало определенного запаса геометрических и арифметических знаний.
Но вот урожай собран. Как в то время отмеривали зерно? Первоначально это делали так, как поступаем и мы при измерении воды или керосина, т. е. мерили его по объему. Выбирали в качестве единицы измерения сосуд определенной вместимости и считали, сколько содержится таких сосудов в куче зерна. Этот первый способ определения объема приводил к вопросу о соотношении между объемами разных тел.
Постепенно люди начали измерять более сложные геометрические фигуры и изучать их свойства.
По дошедшим до нас египетским папирусам и древневавилонским текстам видно, что уже за 2 тыс. лет до н. э. люди умели определять площади треугольников, прямоугольников, трапеций, приближенно вычислять площадь круга. Они знали также формулы для определения объемов куба, цилиндра, конуса, пирамиды и усеченной пирамиды. Сведения по геометрии вскоре стали необходимы не только при измерении земли. Развитие архитектуры, а несколько позднее и астрономии предъявило геометрии новые требования. И в Египте, и в Вавилоне сооружались колоссальные храмы, строительство которых могло производиться только на основе предварительных расчетов. В VI в. до н. э. в одном из древнегреческих государств на острове Самос был построен водопровод, по которому вода в город поступала из источника, лежащего за горой Кастро. Водопровод проходил через туннель длиной в 1 км. Замечательно, что туннель этот начали рыть с обеих сторон одновременно и оба участка его почти точно сошлись под землей! Это значит, что предварительно было определено направление туннеля, т. е. решена задача вычислительной геометрии, которая и сейчас считается в инженерном деле отнюдь не простой. При этом строители древно-
293
сти должны были пользоваться какими-то чертежами, должны были знать учение о подобии. Еще до Пифагора были хорошо известны частные случаи теоремы, носящей его имя. А именно: было известно, что если длины сторон прямоугольного треугольника могут быть выражены в целых числах, то квадрат длины гипотенузы равен сумме квадратов длин катетов. Знали уже и обратную теорему: если а, b и с такие целые числа, что c² =a² +b² (например, а=3, 5=4, с=5), то треугольник со сторонами а, b, с будет прямоугольным. Именно в таком виде
«теорема Пифагора» и обратное ей предложение были известны в Вавилоне.
И все же, несмотря на то что человечество накопило такие обширные знания, геометрия как наука еще не существовала.
Дело в том, что в странах Древнего Востока, о которых шла речь, геометрические знания напоминали сборник мало связанных между собой полезных рецептов, их даже и излагали так, как в наши дни кулинарные рецепты или советы по домоводству. Для решения задачи приводился рецепт, в правильности которого можно было убедиться на конкретных примерах. Общие предложения не доказывались.
Примерно такой же характер имели геометрические знания и в древней Греции в VII - VI вв. до н. э. Греческая культура была более молодой, и поэтому многие научные сведения греки заимствовали у египтян и вавилонян. Именно здесь, в Греции, в VI в. до н. э. и произошло коренное преобразование способа изучения геометрии, здесь и возникла она как наука.
Это было время установления демократии в большинстве греческих городов-государств, время бурного развития общественно-политической жизни Греции и появления научно-философских школ. В этих школах ученые впервые в истории человечества пытались понять и объяснить устройство мира с естественнонаучной и философской точек зрения. До этого в странах Древнего Востока господствовали догматы религии, в которые надо было верить, обсуждать их было нельзя. В Греции же каждая из школ старалась доказать правильность своей теории и опровергнуть противников, показав, что их доводы логически противоречивы. Логические рассуждения получили в это время широкое применение не только в естественных науках и философии, но и в судах, и в народных собраниях.
Особенно большую роль сыграли логические рассуждения в геометрии - они-то и сделали из собрания геометрических фактов стройную науку. Сами греки связывали рождение геометрии с деятельностью Пифагора и его школы. О Пифагоре у нас нет почти никаких достоверных сведений; уже в древности его имя было окружено самыми фантастическими легендами. Из-
В последовательности натуральных чисел зачеркните простое число р и все кратные ему. Из оставшихся чисел образуйте такую последовательность:
единица, сумма первых двух чисел, сумма первых трех чисел и т. д.
В получившейся последовательности снова зачеркните числа, кратные p , и опять образуйте последовательность сумм таким же способом, как первый раз.
Если указанную операцию выполнить р раз, причем в последний раз уже не производить никаких вычеркиваний, то образовавшиеся числа будут p-ми степенями натуральных чисел.
Пример. Пусть р = 3. Тогда из последовательности натуральных чисел надо вычеркнуть числа
3, 6, 9, 12,...; из оставшейся последовательности
1, 2, 4, 5, 7, 8, 10, 11,... образуем новую последовательность, как указано:
1, 3, 7, 12, 19, 27, 37, 48,..., вычеркивая числа, кратные 3, составляем третью последовательность:
1, 8, 27, 64,...,
а это и есть последовательность кубов чисел натурального ряда: 1³, 2³, 3³, 4³, ..., как и было обещано!
294
вестно только, что Пифагор переселился около середины VI в. до н. э. с острова Самос в Южную Италию (так называемую Великую Грецию), где находились богатые греческие города-колонии, и основал там союз, имевший и политические и научные цели. Мы знаем выдающихся математиков V в. до н. э., которые называли себя пифагорейцами, Поэтому у нас есть все основания говорить о пифагорейской математической школе, хотя мы не знаем в точности, какие открытия были сделаны самим Пифагором, а какие принадлежат его последователям.
Что же сделали пифагорейцы в геометрии? Прежде всего они начали строить геометрию как абстрактную науку, изучающую общие свойства неких идеальных фигур, которые «в чистом виде» в природе не встречаются. Так в геометрию были введены линии, имеющие только длину, но не имеющие ширины; точки, не имеющие ни длины, ни ширины; фигуры, составленные из таких линий, и т. д. Эти новые геометрические объекты являются отвлечениями, абстракциями от формы реальных физических тел. Например, прямая линия могла возникнуть как абстракция от формы туго натянутой веревки, струны, луча света и т. п. Но ясно, что мы никогда не сможем построить отрезок идеальной прямой: как бы точно мы его ни вычертили тушью или мелом, стоит только посмотреть на рисунок в сильную лупу, чтобы убедиться, что это вовсе не отрезок прямой, а неровная палочка из туши или мела.
Создание отвлеченных геометрических понятий было вовсе не легким делом. Далеко не все мыслители древности понимали их пользу. Так, например, софист Протагор не признавал геометрических абстракций. Он говорил, что никто не видел линий без ширины, не видел, чтобы круг касался линейки только в одной точке - касание всегда будет происходить по маленькому отрезочку, поэтому таких вещей и не существует.
Однако новая точка зрения на геометрию позволила в очень короткий срок добиться таких удивительных результатов, что большинство ученых признали эти абстракции и начали с ними оперировать. Как же они это делали? Как вообще можно изучать свойства тех идеальных фигур, с которыми имеет дело геометрия?
Величайшим достижением древних греков было то, что они создали метод для изучения геометрических абстракций, введя в математику логические доказательства.
Рассмотрим, например, как можно установить, что сумма углов треугольника точно равна 2d.
Непосредственным измерением это сделать нельзя, во-первых, потому, что на практике мы никогда не имеем дела с идеальными треугольниками, и, во-вторых, потому, что измерение углов на практике всегда производится с определенной степенью точности, например с точностью до 1' или 1".
Но если бы даже мы и могли измерять идеальные треугольники (с помощью идеальных инструментов!), то и тогда мы не могли бы установить теорему о сумме углов любого треугольника, потому что различных треугольников бесконечно много, невозможно перебрать их все!
Но все сказанное можно дословно повторить и о любой другой теореме: она относится не к одной определенной геометрической фигуре (например, к треугольнику со сторонами 3, 4, 5), а к целому классу фигур (например, ко всем треугольникам, или ко всем прямоугольным треугольникам, или ко всем равнобедренным треугольникам), причем каждый такой класс состоит из бесконечного множества отдельных фигур.
Древнегреческие ученые понимали, что установить правильность какого-нибудь свойства для всех фигур некоторого класса можно только с помощью логического доказательства. Но как построить такую систему геометрии, в которой все правильные предложения можно было бы доказать? И можно ли построить такую систему?
Во-первых, ясно, что все правильные предложения доказать нельзя. Действительно, вспомним, как доказываются геометрические предложения. При этом обычно опираются на некоторые другие предложения, которые были доказаны раньше. Эти предложения в свою очередь доказываются ссылками на какие-то третьи теоремы и т. д. Эти ссылки мы могли бы продолжать до бесконечности, и процесс доказательства при этом никогда бы не закончился. Как же быть? Это обстоятельство заметили еще в древности, о нем говорил, например, Аристотель (IV в. до. н. э.). И вот геометры пришли к удивительно смелой мысли, что все геометрические свойства тел нашего пространства можно вывести из небольшого числа основных предложений - аксиом. Эти предложения принимались без доказательств, их справедли-
295
вость подкреплялась многовековым опытом. Усилия многих геометров были направлены на то, чтобы отыскать все аксиомы, необходимые для построения геометрии. Система, в которой каждое предложение выводится на основании логических правил из конечного числа предложений, принятых без доказательства, и получила название дедуктивной.
Первую такую систему геометрии - «Начала» - пытался построить еще в V в. до н. э. Гиппокарт Хиосский. Было еще несколько попыток такого рода, но наиболее совершенная из них знаменитые «Начала» Евклида, которые были написаны около 300 г. до н. э. и служили в течение более 2 тыс. лет образцом математической строгости.
Евклид разделил предложения, принятые без доказательства, на аксиомы и постулаты. В качестве постулатов он выбрал предложения, в которых утверждалась возможность выполнения некоторых простейших геометрических построений, например: 1) через две точки всегда можно провести прямую линию, 2) из данной точки данным радиусом можно описать окружность. Как нетрудно видеть, это именно те построения, которые можно сделать с помощью циркуля и линейки. Всякое построение в геометрии Евклида осуществляется с помощью последовательного выполнения простейших построений: проведения прямых, окружностей и отыскания их точек пересечения, поэтому геометрия Евклида есть геометрия циркуля и линейки.
Среди постулатов Евклида особое место занимает так называемый V постулат о параллельности. В «Началах» он формулируется так: если две прямые, лежащие в одной плоскости, пересечены третьей и если сумма внутренних
односторонних углов меньше 2d, то при продолжении прямые пересекутся с той стороны, где эта сумма меньше 2d (рис. 1). Этот постулат сыграл огромную роль в дальнейшем развитии геометрии, о чем мы будем говорить дальше.
Кроме постулатов, Евклид принял также некоторые общие предложения - аксиомы: 1) две величины, порознь равные третьей, равны между собой; 2) если к равным величинам прибавить равные, то и суммы будут равны; 3) целое больше части и др.
На основе своих постулатов и аксиом Евклид развил всю планиметрию, а с ее помощью построил элементы алгебры и учение о квадратных уравнениях. В его сочинении содержатся также общая теория отношений, которая применяется в учении о подобии, теория чисел, метод определения площадей и объемов и основы стереометрии. Венчает «Начала» учение о правильных выпуклых многогранниках, т. е. таких, все грани которых являются равными правильными многоугольниками и все многогранные углы при вершинах тоже правильные и равные. Евклид доказал, что существует пять правильных многогранников: тетраэдр, куб, октаэдр, икосаэдр и додекаэдр - и никаких других правильных многогранников не существует (рис. 2).
Можно сказать, что в «Началах» Евклида были заложены основы не только геометрии, но и всей античной математики.
На новую, более высокую ступень исследования основ геометрии ученые поднялись только в XIX в. Тогда было выяснено, что Евклид перечислил не все аксиомы, которые на самом деле нужны для построения геометрии. В действительности при доказательствах он ими пользовался, хотя и не формулировал их. Однако все это нисколько не умаляет роли Евклида, который первым показал, как можно и как нужно строить математическую теорию. Созданный им дедуктивный метод прочно во-
296
Рис. 2. Правильные многогранники.
шел в математику. В этом смысле все последующие математики, вплоть до наших современников, являются учениками Евклида.
При построении дедуктивной системы геометрии выяснилось, что доказательства служат не только для того, чтобы установить истинность некоторого предложения, но и для выявления взаимосвязей между предложениями. Так, при анализе доказательства предложения о том, что сумма углов треугольника равна 2 d, оказалось, что оно зависит от V постулата Евклида, тогда как, например, теорема о том, что внешний угол треугольника больше каждого внутреннего, с ним не смежного, от постулата параллельности не зависит.
Таким образом, доказательства помогают уяснить существо, смысл математических предложений. В частности, можно в евклидовой геометрии выделить все те предложения, которые доказываются без постулата параллельности,- они составляют так называемую абсолютную геометрию.
Математики все время испытывали некоторую неудовлетворенность, связанную с постулатом о параллельности, который, как мы видели, формулировался довольно сложно. Казалось, что его можно доказать, вывести из других постулатов и аксиом. Начиная с глубокой древности и до конца XVIII в. многие геометры пытались доказать этот постулат как теорему.
Однако все доказательства V постулата, которые были придуманы, либо содержали прямую ошибку, либо опирались на новое предложение, которого не было среди постулатов и аксиом Евклида. При более тщательном анализе всегда оказывалось, что это новое предложение равносильно постулату о параллельности, т. е. из него можно вывести этот постулат и, наоборот, из V постулата можно получить это новое предложение. К началу XIX в. вопрос о V постулате казался безнадежно запутанным. Но как раз в 20-х годах прошлого века было получено совершенно неожиданное решение этого многовекового вопроса. Это решение было связано с совершенно новым взглядом на геометрию, к которому пришли независимо друг от друга три великих геометра: Н. И. Лобачевский, К. Ф. Гаусс и Я. Бояи.
297
Впервые в печати решение вопроса появилось в работе Н. И. Лобачевского в 1829 - 1830 гг. (эта работа была доложена Лобачевским в Казанском университете еще в 1826 г.), и несколько позже - в 1832 г.- было опубликовано исследование Бояи. Гаусс вообще не опубликовал те смелые выводы, к которым пришел.
Новая идея, которая легла в основу решения, состояла в следующем: геометрия Евклида не является единственной возможной геометрией, можно построить и другие системы геометрии, столь же стройные и непротиворечивые, как евклидова. При этом и Н. И. Лобачевский, и К. Ф. Гаусс были глубоко убеждены, что новая геометрия получит применение для описания и изучения геометрических свойств нашего пространства.
Такой взгляд противоречил двухтысячелетней традиции, благодаря которой сложилось убеждение, что геометрия Евклида столь же естественна, как смена дня и ночи, и что только она описывает пространственные соотношения между реальными телами.
Как же строить новые геометрические системы? В XVIII в. геометры придумали новый способ доказательства V постулата. Они предполагали, что V постулат неверен, и старались прийти к противоречию, как это делается при доказательствах от противного. Действительно, если V постулат можно вывести из других постулатов и аксиом геометрии Евклида, т. е. он является теоремой, то предположение, что он неверен, должно было бы привести нас к противоречию. Однако как ни пытались геометры получить противоречие, им этого сделать не удавалось. Они получали все новые и новые следствия; некоторые из них выглядели парадоксально, например: сумма углов треугольника у различных треугольников различна, но всегда меньше 2 d ; линия, равноотстоящая от некоторой прямой (эквидистанта), сама не является прямой; не существует подобных треугольников и вообще подобных фигур. Однако ни одно из следствий не противоречило другому следствию и остальным аксиомам евклидовой геометрии.
Лобачевский, Гаусс и Бояи пришли к убеждению, что противоречия и не получится, потому что V постулат не является теоремой в евклидовой геометрии. Что же в таком случае представляют полученные следствия? Оказывается - теоремы новой геометрии! Таким образом, для построения новой геометрии нужно было заменить V постулат другим и вывести из новой системы постулатов и аксиом возможные следствия. Они-то и будут теоремами новой геометрии.
V постулату Евклида часто придают такую форму: через точку вне прямой в плоскости, определяемой этой точкой и этой прямой, можно провести только одну прямую, не пересекающую данной.
Если этот постулат не имеет места, то это означает, что: 1) либо можно провести по крайней мере две прямые, не пересекающие данной (рис. 3), 2) либо таких прямых не существует вовсе (т. е. вообще нет параллельных прямых).
Второе из этих предположений легко приводится к противоречию с другими аксиомами и постулатами Евклида. Первое же Н. И. Лобачевский выбрал в качестве нового постулата о параллельности. Он построил стройную систему геометрии, которая носит теперь его имя. При этом Н. И. Лобачевский показал, что геометрия Евклида может быть получена как предельный случай новой геометрии.
Исследования Н. И. Лобачевского открыли новую эру в истории геометрии. Если до этого казалось, что в основном в геометрии все сделано уже самим Евклидом, то после создания неевклидовой геометрии открылись широкие возможности для новых геометрических изысканий.
В 60-х годах прошлого века немецкий математик Риман предложил новый метод построения всех неевклидовых геометрий, в которых можно мерить длины, площади, углы, объёмы (так называемых метрических геометрий). При этом он не ограничился случаем трехмерного пространства, а строил геометрии пространств любого числа измерений. Интересно отметить, что, в частности, он построил такую геометрию, в которой нет параллельных прямых. Конечно, для построения такой геометрии пришлось отказаться от некоторых других аксиом евклидовой геометрии.
Эта геометрия похожа на сферическую, ее называют эллиптической или геометрией Ри-
298
мана (в узком смысле слова, в отличие от общих римановых геометрий). В этой геометрии, так же как в геометрии Лобачевского, нет подобных фигур, но сумма углов треугольника в ней всегда больше 2d, а длины прямых линий ограничены.
Были предложены и другие методы построения новых геометрий.
Но в связи с новыми геометриями встали и другие вопросы: геометрия Лобачевского отличается от евклидовой постулатом о параллельности. Что будет, если заменять и другие постулаты? Всегда ли при этом будут получаться новые системы геометрии? В каких случаях новые системы будут непротиворечивыми, т. е. в них нельзя доказать некоторую теорему и одновременно доказать, что эта теорема неверна?
Для ответа на эти вопросы ученые прежде всего вновь обратились к исследованию геометрии Евклида с тем, чтобы найти все аксиомы, нужные для ее построения, а затем уже изучить связи между этими аксиомами, посмотреть, что будет, если отбросить одну или несколько из них и заменить другими. Многие математики конца прошлого века занимались этой проблемой, но впервые ее удалось решить немецкому математику Д. Гильберту в 1899 г. В его книге «Основания геометрии» была изучена первая полная система аксиом геометрии Евклида и исследованы вопросы, о которых мы говорили выше. Это направление исследований привело к созданию современного аксиоматического метода, значение которого трудно переоценить.
Неевклидовы геометрии открыли новую эру не только в математике, но и в физике. Как и предвидели создатели этих геометрий, они сделались незаменимым математическим аппаратом многих важнейших частей современной физики, особенно теории относительности.
Более подробно о новых геометриях вы можете узнать из статьи «О различных геометриях».
Итак, мы видим, что возникновение геометрии как науки далеко не закончилось построением системы евклидовой геометрии. Это было только начало, блестящее продолжение которого осуществилось в XIX в.
В настоящее время геометрия представляет большую, широко разветвленную науку, тесно связанную со всеми остальными разделами математики.
Прежде чем завести разговор о геометрических преобразованиях, остановимся на вопросе о самом содержании предмета геометрии; впоследствии мы увидим, что к понятию геометрического преобразования этот вопрос имеет самое непосредственное отношение.
Геометрия изучает свойства плоских фигур и пространственных тел. Однако в геометрии рассматриваются вовсе не все свойства фигур или тел. Ясно, например, что цвет или вес тела для геометра безразличен - геометрические свойства куба останутся одними и теми же независимо от того, идет ли речь о металлическом кубе или о кубе, сделанном из фанеры и окрашенном в красный цвет. (Заметим, что физические свойства этих двух кубов во многом будут различны.) Также и расстояние от вер-
шины изображенного на доске треугольника до края доски не интересует геометра. Один из двух равных между собой треугольников (рис. 1) расположен заметно ближе к краю MQ доски, чем второй; однако все геометрические свойства этих треугольников - их соответственные стороны, углы, высоты, медианы, площади, радиусы вписанной и описанной окружностей, расстояние от центра описанной окружности до точки пересечения медиан и т. д.- будут одинаковыми. Как же охарактеризовать тот круг свойств фигур и тел, который интересует геометра?
299
Рис. 4. Равные фигуры.
Все свойства тел, которые рассматриваются в геометрии, полностью определяются формой и размерами тела и никак не зависят от его расположения. Другими словами, это означает, что каждые две равные фигуры или два равных тела обладают в точности теми же самыми геометрическими свойствами; поэтому геометр не может иметь никаких оснований для того, чтобы как-либо различать эти фигуры или тела. Это обстоятельство подразумевается и самим названием «равные тела». Ведь «равные числа» в арифметике - это не что иное, как одно и то же число; так, 1/2 и 3/6 это одно и
то же число, только записанное по-разному. Точно так же в геометрии слова «равные фигуры» иногда заменяют выражением «одна и та же фигура». Так, например, говорят, что задача построения треугольника А B С по двум сторонам ВС=а и АС= b и углу АСВ= g имеет единственное решение (рис. 2). На самом деле существует, конечно, очень много (даже бесконечно много!) треугольников, имеющих две стороны длин а и b и заключенный между ними угол величины у (рис. 3). Однако все эти треугольники равны между собой; поэтому мы их принимаем за один треугольник.
Вспомним теперь, какие фигуры или тела считаются в геометрии равными. Две фигуры F и F' (рис. 4) называются равными, если при наложении одной из них на другую они совпадают всеми своими точками, другими словами - если существует движение, при помощи которого можно совместить фигуру F с фигурой F'. Таким образом, само определение равенства фигур (или тел) связано с понятием движения. Учитывая определение равенства фигур, мы можем сказать, что фигуры, получающиеся одна из другой движением, считаются в геометрии одинаковыми, не различаются между собой; все геометрические свойства одной из этих фигур совпадают с геометрическими свойствами другой фигуры. Последнее обстоятельство можно принять за определение геометрических свойств, т. е. тех свойств фигур и тел, которые изучаются геометрией: геометрия изучает те (и только те!) свойства фигур и тел, которые сохраняются при движениях.
Приведем несколько примеров движений плоских фигур.
Параллельным переносом называется движение, при котором фигуру как целое перемещают в определенном направлении, не поворачивая ее.
Параллельный перенос характеризуется направлением, которое задается указанием некоторой прямой l с поставленной на этой прямой стрелкой и расстоянием а, на которое переносятся фигуры. Каждую точку А параллельный перенос переводит в такую точку А', что АА' || l (причем направление от точки А к точке
300
А' совпадает с тем, которое указано стрелкой на прямой l) и АА'=а (рис. 5).
Поворот (вращение) вокруг точки О на угол а характеризуется тем, что каждая точка А переходит в такую точку А', что ОА= O А' и Ð АОА'= a . (рис.6); при этом должно быть указано также и направление поворота, которое может совпадать с направлением вращения часовой стрелки или быть противоположно ему.
Рис, 6. Поворот вокруг точки О на угол a .
Поворот вокруг точки О на угол 180° называется также симметрией относительно точки О; здесь каждая точка А переходит в такую точку А', что О есть середина отрезка АА' (рис. 7).
Еще один важный пример движения представляет собой симметрия относительно прямой l ; это движение можно реализовать, перегнув лист бумаги по прямой l. Симметрия относительно прямой l переводит каждую точку А в такую точку А', что отрезок АА' перпендикулярен прямой l и делится этой прямой пополам (рис. 8). Каждый легко может получить симметричные фигуры, сделав кляксу на листе бумаги и затем перегнув лист (рис. 9).
Эти примеры достаточно хорошо характеризуют содержание понятия «движение». Каждое движение задается указанием определенного закона или правила, указывающего, как найти точку А', в которую это движение
Рис. 7. Симметрия относительно точки O.
переводит произвольную точку А. На рис. 10 перечислены правила, относящиеся к указанным выше движениям. Вообще, задание правила, позволяющего перейти от произвольной точки А к новой точке А' (которая может и совпадать с исходной точкой А, определяет геометрическое преобразование.
Под фигурой в геометрии понимают совокупность, или множество, точек; так, окружность с центром О и радиусом r есть совокупность таких точек М, что ОМ= r (рис. 11); отрезок с концами A и В есть совокупность таких точек М, что АМ+МВ=АВ (рис. 12); прямую можно охарактеризовать как совокупность таких точек М, что АМ=ВМ, где точки А и В заданы (рис. 13).
Геометрическое преобразование переводит каждую точку А, входящую в состав фигуры F, в новую точку А'. При этом совокупность точек фигуры F переходит в некоторую новую совокупность точек, образующую фигуру F'. Про
301
Рис. 10. Правила, по которым точка А переводится в точку А'.
302
фигуру F' говорят, что она получается рассматриваемым преобразованием из фигуры F (рис. 14).
Движения представляют собой простейшие геометрические преобразования - такие, которые переводят каждую фигуру F в равную ей фигуру F', т. е. сохраняют форму и размеры фигур.
Преобразования, сохраняющие форму фигур, но, возможно, изменяющие их размеры, называются преобразованиями подобия. Каждую фигуру F преобразование подобия переводит в подобную ей фигуру F', представляющую собой увеличенную или уменьшенную копию первоначальной фигуры; все размеры фигуры F' равны соответствующим размерам фигуры F, умноженным на одно и то же число k (рис. 15). Это
Рис. 15. Подобные фигуры.
число называется коэффициентом подобия двух фигур. Подобные фигуры можно получить, например, поместив под лампой вырезанную из куска картона фигуру F, плоскость которой параллельна поверхности стола; в таком случае тень F', отбрасываемая этой фигурой на стол, будет подобна F (рис. 16). Более «математический» пример преобразования подобия представляет собой гомотетия с центром О и коэффициентом k, переводящая каждую точку А в такую точку А' луча ОА, что
OA'/OA=k (рис. 17).
Некоторые свойства фигуры F', подобной фигуре F, будут отличаться от свойств фигуры F; так, например, гомотетия с коэффициентом 2 переводит фигуру ABCD в фигуру
A'B'C'D', площадь которой в 4 раза больше площади фигуры ABCD (рис. 17). Но большинство свойств фигуры F' будет совпадать со свойствами фигуры F : так, все имеющиеся на фигуре F' углы будут равны соответствующим им углам, имеющимся на фигуре F ; отношение расстояний между какими-либо точками фигуры F' будет равно отношению расстояний между соответственными точками фигуры F (см. рис. 15, где, скажем, AB/CD = A'B'/C'D')
и т. д. Таким образом, преобразования подобия меняют свойства геометрических фигур очень
1
Не вычисляя площадей треугольников со сторонами а=5, b=5, с=b, a1=5, b1=5, с1=8, выяснить, равновелики ли они.
2
Найти три равновеликих прямоугольных треугольника при условии, что все 9 сторон - различные целые числа.
3
Трех плоских разрезов достаточно, чтобы перестроить этот брусок в куб.
Как добиться наименьшего возможного числа частей, на которые распадается брусок? Ответы на стр. 321.
303
мало: окружность они переводят снова в окружность, квадрат - в квадрат, равнобедренный треугольник с углом при вершине в 40° - снова в равнобедренный треугольник с углом при вершине в 40° и т. д.
Эти свойства преобразований подобия иногда могут быть использованы для решения содержательных геометрических задач. Поставим, например, такую задачу: определить, что представляет собой множество середин всех
отрезков AM, где точка А фиксирована, а точка М пробегает, скажем, равностороннюю гиперболу G (график обратной пропорциональной зависимости). Очевидно, что искомое множество точек образует фигуру G', гомотетичную гиперболе G с центром гомотетии А и коэффициентом гомотетии1 /2. Отсюда следует, что это будет точно такая же гипербола, только в 2 раза «меньшая» (такая, что расстояние между двумя точками гиперболы G' в 2 раза меньше расстояния между соответствующими точками гиперболы G ; рис. 18).
Рассмотрим тень, отбрасываемую на солнце вырезанной из картона фигурой F на плоскость a, не обязательно параллельную этой фигуре (рис. 19). Геометрически переход от фигуры F к ее тени F' описывают как параллельное проектирование, переводящее каждую точку А фигуры F в такую точку А ' плоскости a, что АА' ║ а, где а - заданная прямая, характеризующая направление проектирования (ибо лучи солнца можно считать параллельными).
Фигура F' может значительно отличаться от первоначальной фигуры F; так, каждый знает, насколько сильно искажены на тени истинная форма и размеры предметов, если солнце стоит достаточно низко (рис. 20). Одна-
304
Одним из видов «движения» является симметрия. Фигуры, которые в результате «движения» переходят в себя, называются симметричными. На рисунке изображены фигуры, обладающие осевой, центральной симметрией и симметрией порядка n (говорят, что фигура обладает симметрией порядка и, если она переходит в себя при повороте вокруг точки - центра симметрии - на угол 360° / n). Определите, к какому из этих трех видов симметрии относится каждая фигура, найдите ось или центр симметрии, а для фигур с симметрией порядка m найдите это число.
Кривые линии, которые получаются при пересечении поверхности прямого кругового конуса плоскостями, не проходящими через его вершину, называются кривыми второго порядка или коническими сечениями. Конические сечения могут быть трех типов:
1) Секущая плоскость пересекает все образующие конуса в точках одной ее полости, линия пересечения есть замкнутая овальная
линия - эллипс; окружность как частный случай эллипса получается, когда секущая плоскость перпендикулярна оси конуса.
2) Секущая плоскость параллельна одной из касательных плоскостей конуса; в сечении получается незамкнутая уходящая в бесконечность кривая - парабола, целиком лежащая в одной полости.
3) Секущая плоскость пересекает обе полости конуса; линия пересечения - гипербола, состоит из двух одинаковых незамкнутых простирающихся в бесконечность частей (ветвей гиперболы), лежащих на обеих полостях конуса.
На рисунках внизу изображены линии, которые описывает точка круга, когда он катится по прямой линии. При этом точка окружности описывает линию с остриями - циклоиду. Всякая точка внутри круга описывает линию без остриев - укороченную циклоиду. А если точка закреплена вне круга на продолжении его радиуса, то она описывает линию с петлями - удлиненную циклоиду.
ко некоторое сходство между фигурой F и ее тенью F ' и тут сохранится. Так, например, каждая, прямая, проведенная в плоскости фигуры F, перейдет снова в прямую линию (рис. 21); параллельные прямые перейдут в параллельные прямые; отношение длин отрез-
Рис. 21. Параллельное проектирование.
ков, принадлежащих одной прямой (но не разным прямым!), при параллельном проектировании сохранится (см. рис. 21, где AB/BC = A'B'/B'C').
Квадрат ABCD параллельное проектирование уже не переведет в квадрат; однако оно переведет его в параллелограмм, который отличается от квадрата не так уж резко.
Геометрические преобразования, обладающие такими свойствами, называются линейными преобразованиями. К числу линейных преобразований относится, например, так называемое сжатие к прямой l, которое описывается так: точку А плоскости сжатие к прямой l переводит в такую точку А', что точки А и А' лежат на одном перпендикуляре к прямой l и PA'/PA =k: где Р - основание перпендикуляра (рис. 22). Постоянное
Рис. 22, Сжатие к прямой.
число k называется коэффициентом сжатия к прямой (при k>l было бы правильнее говорить о «растяжении» от прямой l). Нетрудно убедиться, что сжатие к прямой также переводит прямую линию снова в прямую, параллельные прямые переводит в параллельные, сохраняет отношения длин отрезков, принадлежащих одной прямой.
Знание свойств, сохраняющихся при линейных преобразованиях, позволяет использовать эти преобразования для доказательства некоторых геометрических теорем. Разумеется, квадрат ABCD и получающийся из него параллельным проектированием параллелограмм A'B'C'D' имеют много разных свойств;
305
306
однако те свойства, которые сохраняются при линейных преобразованиях, совпадают у квадрата и у параллелограмма. Выберем произвольную точку Е на диагонали АС квадрата ABCD и проведем через нее отрезки MN ║ АВ и PQ ║ ВС (рис. 23, а). Нетрудно видеть, что прямая А С явится осью симметрии полученного чертежа; поэтому прямые MQ и PN (симметричные относительно прямой АС!) пересекутся на прямой АС. А отсюда вытекает, что и отрезки M'N' ║ А'В' и P'Q' ║ В'С', пересекающиеся на диагонали А'С' параллелограмма A'B'C'D', отсекают от параллелограмма меньшие параллелограммы M'D'Q'E' и N'B'P'E', диагонали M'Q' и N'P' которых пересекаются на прямой А'С' (рис. 23, б). Доказать это, не пользуясь линейными преобразованиями, было бы затруднительно!
Рассмотрим еще и такой пример. Ясно, что каждый треугольник АВС можно параллельным проектированием перевести в равносторонний треугольник АБС' (рис. 24; треугольники А B С' и ABC расположены в разных плоскостях; СС ' - направление проектирования). При этом медианы треугольника А B С переходят в медианы треугольника А B С' (это следует из свойств параллельного проектирования). Но медианы равностороннего треугольника являются одновременно и биссектрисами; поэтому они пересекаются в одной точке - центре окружности, вписанной в треугольник А B С'. А отсюда следует, что также и медианы исходного треугольника А B С пересекаются в одной точке. Это доказательство теоремы о точке пересечения медиан треугольника является, вероятно, простейшим!
Вот еще пример на использование свойств линейных преобразований. Линейное преобразование уже не переводит окружность снова в окружность - оно переводит ее в другую линию, называемую эллипсом (рис. 25). Эллипс можно определить как линию, получающуюся при сечении кругового цилиндра произвольной плоскостью (рис. 26); это означает, что эллипс образуется из окружности в результате параллельного проектирования.
Заметим, что центр О окружности S является ее центром симметрии, т. е. что все проходящие через О хорды окружности S делятся этой точкой пополам (рис. 27, а). Линейные преобразования не сохраняют отношения длин отрезков, принадлежащих разным прямым; поэтому проходящие через точку О радиусы окружности S переходят в «радиусы» эллипса S', пересекающиеся в одной точке О', но уже не равные между собой (рис. 27, б). Но отношение длин отрезков, принадлежащих одной прямой, при линейном преобразовании сохраняется, и поэтому все проходящие через точку О' хорды эллипса S' делятся в этой точке пополам. Таким образом, мы убеждаемся, что каждый эллипс S' обладает центром симметрии О'; эту точку О' часто называют просто центром эллипса.
Число примеров подобного рода можно увеличить. Проведем из точки М к окружности S касательные МА и MB (рис. 28. а). Мы знаем, что МА= MB ; что ОМ ^ АВ, где О - центр окружности S', что АК=КВ, где К - точка пересечения ОМ и АВ (все эти факты следуют из того, что прямая ОМ есть ось симметрии; см. рис. 28, а). Равенство отрезков МА и М B не может быть перенесено на эллипс (отношение длин отрезков, принадлежащих разным прямым, не сохраняется при параллельном проектировании); перпендикулярность прямых ОМ и АВ также характерна именно для окружности (углы не сохраняются при линейных преобразованиях). А вот то обстоятельство, что отрезки АК и К B , принадлежащие одной прямой, равны между собой, имеет место и в случае эллипса: если из внешней точки М' провести к эллипсу S ' с центром О' касательные М'А' и М'В', то прямая О'М' разделит хорду А'В' пополам (рис. 28, б).
Докажем еще, что середины всех параллельных между собой хорд эллипса принадлежат одной прямой, проходящей через центр эллипса (диаметр у эллипса). В самом деле, пусть наш
Чтобы изготовить модель многогранника из куска картона, надо прежде всего начертить развертку требуемого многогранника. На рисунке изображена правильная пирамида, все грани которой - равносторонние треугольники, и две развертки такой пирамиды. Сгибая каждую развертку по пунктирным линиям, можно построить модель пирамиды. Какие-либо другие формы разверток пирамиды, все грани которой равносторонние треугольники, невозможны. Куб в этом смысле богаче: у него более десятка разверток различных форм. А сколько же все-таки точно? Начертите все развертки куба.
Решение на стр. 321.
307
Рис. 29.
эллипс S' получился линейным преобразованием (скажем, центральным проектированием) из окружности S. Середины всех параллельных между собой хорд окружности принадлежат одной прямой, проходящей через центр О окружности и перпендикулярной проведенным хордам (рис. 29, а). При линейном преобразовании параллельные между собой хорды окружности S переходят в параллельные хорды эллипса S', а диаметр d окружности, делящий ее хорды пополам,- в диаметр d' эллипса, делящий пополам параллельные хорды эллипса (рис. 29, b).
Рассмотрим теперь тень, отбрасываемую вырезанной из картона фигурой, помещенной под электрической лампочкой, на поверхность стола, не обязательно параллельную плоскости фигуры (рис. 30). Эта тень может очень сильно отличаться от исходной фигуры - однако начерченная на фигуре прямая линия перейдет при этом снова в прямую.
Здесь мы имеем дело с центральным проектированием фигуры из точки на плоскость стола, переводящим каждую точку фигуры в точку пересечения прямой с плоскостью стола.
Центральное проектирование доставляет нам пример проективного преобразования. Проективные преобразования гораздо сильнее меняют свойства фигур, чем линейные; так, квадрат ABCD они могут перевести в произвольный четырехугольник A'B'C'D' (рис. 31). Однако и здесь можно указать ряд свойств геометрических фигур, сохраняющихся при центральных проектированиях, и воспользоваться
этим для вывода интересных свойств произвольных четырехугольников из свойств квадрата. Проективные преобразования переводят окружность в так называемые конические сечения. Это название связано с тем, что если центральное проектирование с центром О переводит окружность S в фигуру S', то S' представляет собой плоское сечение кругового конуса с вершиной О (рис. 32). Можно доказать, что к числу конических сечений принадлежат как рассмотренный выше эллипс, так и изучаемые в средней школе гипербола (график обратной пропорциональной зависимости) и парабола (график функции y =х²). Используя это обстоятельство, а также общие свойства проективных преобразований, можно доказать, что гипербола и парабола обладают рядом интересных свойств, родственных свойствам окружности и эллипса.
Рис. 32. образование конических сечений
308
Немецкий математик Ф. Клейн в конце прошлого столетия предложил положить геометрические преобразования в основу классификации всех свойств геометрических фигур и тел. Он предложил различать геометрические свойства по тем преобразованиям, при которых эти свойства сохраняются. К одной группе при этом будут относиться те свойства, которые сохраняются лишь при движениях фигур; сюда относятся все свойства, связанные с расстояниями между точками, и все теоремы, в которых фигурируют длины или площади (например, теорема: площадь треугольника равна половине произведения длины основания на длину опущенной на основание высоты). В другую группу попадут свойства, сохраняющиеся при преобразованиях подобия, например все свойства, связанные с величинами углов; к этой группе свойств относится, скажем, известное свойство прямоугольного треугольника с углом в 30° (ведь отношение длины гипотенузы к длине меньшего катета также сохраняется при преобразованиях подобия!). Еще одну группу составят свойства геометрических фигур, сохраняющиеся при линейных преобразованиях. Далее можно будет рассмотреть свойства фигур, сохраняющиеся при проективных преобразованиях,
и т. д. Так как линейные преобразования изменяют свойства фигур сильнее, чем движения, то свойства, сохраняющиеся при этих преобразованиях, следует считать более глубокими; с этой точки зрения свойство треугольника, выражаемое теоремой: «медианы треугольника пересекаются в одной точке», оказывается более глубоким, чем, скажем, аналогичное свойство высот треугольника. Еще более глубокими следует считать те свойства фигур, которые сохраняются при проективных преобразованиях, очень сильно изменяющих фигуру.
Такая классификация геометрических теорем (Клейн даже говорил об отдельных «геометриях», охватывающих изучение свойств фигур, сохраняющихся при тех или иных преобразованиях) поясняет сказанное выше об использовании геометрических преобразований для доказательства теорем. Все свойства, сохраняющиеся при линейных преобразованиях, будут одинаковы для окружности и для эллипса; поэтому при рассмотрении их мы всегда можем ограничиться изучением окружности, являющейся частным случаем эллипса (окружность - это сечение кругового цилиндра плоскостью, параллельной основанию цилиндра). Точно так же при изучении соответствующих свойств треугольника мы можем считать его равносторонним,
Феликс Клейн.
при изучении свойств параллелограмма - принять его за квадрат и т. д. При изучении проективных свойств произвольного четырехугольника можно считать его квадратом, а при изучении проективных свойств конического сечения - принять это коническое сечение за окружность и т. д. Таким образом, точка зрения Клейна, выделяющая ряд отдельных ветвей геометрии, может существенно помочь при доказательстве геометрических теорем.
Чтобы разрезать куб на 27 равных кубиков, надо сделать 6 разрезов. Можно ли уменьшить число разрезов, если позволить после каждого разрезания перекладывать части?
Ответ на стр. 321.
309
Поверхность кольца, надеваемого на палец, имеет две стороны. Одной стороной она соприкасается с пальцем, вторая сторона наружная. У этих сторон две границы (два края), каждая имеет форму окружности. Если какая-нибудь букашка захочет переползти с наружной стороны кольца на внутреннюю, то она при этом непременно должна пересечь ту или другую границу.
Немецкий математик А. Мебиус указал простую модель поверхности совсем другого фасона - односторонней поверхности. Ее легко приготовить, перекрутив на пол-оборота один конец прямоугольной бумажной полоски и приклеив его к другому концу той же полоски. Эту модель с той поры так и называют: лист Мебиуса.
Чтобы наглядно удостовериться в том, что у поверхности листа Мебиуса только одна сторона, возьмите карандаш и начните последовательно закрашивать лист, не отрывая карандаша от поверхности листа и не пересекая края листа. Когда вернетесь к тому месту, с которого начали, вы увидите, что окажется окрашенной вся поверхность листа, хотя его край вы и не пересекали ни разу.
Возьмите несколько листов плотной бумаги (например, обложки старых журналов большого формата), клей, ножницы и исследуйте «поведение» листа Мебиуса и других моделей, изготовляемых из прямоугольных полосок бумаги, если разрезать их по линиям вдоль края.
1. Что получится, если обыкновенное (не перекрученное) бумажное колечко разрезать вдоль его средней линии? Очевидно, два колечка, причем длина окружности каждого будет такой же, как длина окружности первоначально взятого колечка. А вот если лист Мебиуса мы также разрежем вдоль его средней линии, то образуется...
Проделайте и посмотрите, что получится.
2. Приготовьте второй лист Мебиуса из достаточно широкой полоски и разрезайте его ножницами так, чтобы линия разреза все время шла вдвое ближе к левому краю первоначальной полоски, чем к правому (линия разреза обойдет лист Мебиуса дважды). Теперь образуются два кольца, но они окажутся сцепленными. Проделайте!
А что получится, если вновь взять бумажную полоску, один ее конец перекрутить на полный оборот (на 360°), приклеить к другому концу и разрезать получившуюся модель по средней линии?
3. Надрежьте концы бумажной полоски поглубже, чем показано на рисунке. Склейте концы А и D.
Пропустите конец В под А и приклейте его к Е. Пропустите конец С между В и А, а конец F между D и Е, после чего склейте концы С и F . Все склеивания концов производите прямо, т. е. без предварительного перекручивания.
Теперь каждый начатый разрез продолжайте вдоль всей модели; получится интересное переплетение трех колец: любые два будут сцеплены друг с другом и оба с третьим кольцом.
Если вы ошибетесь и конец С приклеите к концу F, не пропустив С между В и А, то после указанного разрезания получится обычная цепь из трех колец.
310
Всем хорошо известно, что выводы элементарной (школьной) геометрии находят широкое применение при решении самых разнообразных практических задач. Знания геометрии необходимы слесарю, инженеру, ученому - всем, кому приходится исследовать свойства различных фигур и тел. Как же геометрия изучает наш реальный мир? Каждому, по-видимому, приходилось слышать выражения «с математической точностью», «как дважды два - четыре». Этими словами обычно принято характеризовать абсолютно точное и неоспоримое. Ниже мы попытаемся выяснить, с какой точностью геометрические теоремы отражают действительное положение вещей в нашем мире. Действительно ли эта точность беспредельна?
Для того чтобы ответить на эти вопросы, нам понадобится внимательно проанализировать, как строится наука геометрия и как эта наука изучает реальный мир.
В учебнике геометрии постоянно изучаются геометрические объекты различной сложности: треугольники, трапеции, параллелограммы, призмы, пирамиды, сферы и т. п., которые должны быть точно охарактеризованы. Это делается в так называемых определениях. Для того чтобы полностью разобрать то или иное произвольно взятое определение, надо знать определения, изложенные в учебнике ранее. Например, чтобы понять определение трапеции, надо заранее знать определение параллельности прямых, определение четырехугольника, а для этого надо знать определение отрезка. Последнее требует знания того, что такое прямая и точка.
Всякое другое определение точно так же в конце концов приводит нас к первой странице учебника геометрии, где мы надеемся найти определения основных геометрических понятий: точки, прямой, плоскости.
Но, увы, нас ожидает разочарование. Оказывается, что и здесь нет точных математических определений точки, прямой и плоскости. В то же время все дальнейшие определения, которые опираются на эти основные геометрические понятия, сформулированы с полной математической строгостью. Такое положение на первый взгляд может показаться весьма странным.
Правда, в начале учебника даются некоторые пояснения того, что же мы понимаем под точкой, прямой и плоскостью. Пояснения эти, однако, ни в какой мере не могут служить точными математическими определениями. Кроме того, эти пояснения нигде далее в геометрии не используются. Они совершенно не нужны для доказательства теорем. Важным является лишь указание на то, что в дальнейшем будут изучаться именно точки, прямые и плоскости.
Что же такое точка, прямая и плоскость?
Отметим сразу же, что нигде в природе не встречаются точки, прямые и плоскости.
Представим себе шарик малого диаметра, скажем в 1 мм. Уменьшим его диаметр вдвое, втрое, ..., в тысячу раз и т. д. Наступит ли момент, когда уже весьма малый шарик можно будет назвать точкой? Нет!
Учитель ставит на доске весьма «жирную» точку. Ученики рисуют в тетради тоже весьма крупные точки. На самом же деле каждый раз изображаются маленькие кружочки. Но точки ли это? Звезды на небе тоже нам представляются «точками», хотя некоторые из них во много раз больше Солнца. А если представить себе шарик столь малым, что его нельзя увидеть ни в один современный микроскоп,- будет ли это точка? Опять нет.
Дело в том, что точка - это не какой-то конкретный предмет. Точка - это абстрактное понятие, которое образовано нашим сознанием в результате длительного изучения весьма малых (или кажущихся малыми при определенных условиях) реальных объектов - шариков, кружочков и т. п. Это абстрактное понятие точки наделяется нами целым рядом свойств, общих для тех конкретных предметов, в результате наблюдения над которыми и возникло понятие точки.
311
Рис. 2. Представление о прямой дает луч света, проходящий через малое отверстие.
Обратимся теперь к понятию прямой. На бумаге изображена линия. Прямая ли она? Как в этом убедиться? Надо приложить линейку, сравнить линию с краем линейки. Но при этом возникает вопрос: прямая ли наша линейка? Каждому, вероятно, приходилось видеть столяра, который для проверки прямизны выстроганной планки рассматривает ее так, как показано на рис. 1. Если линейка не прямая, на ней есть изъяны, это будет видно на свет. Таким образом, проверяя прямизну сделанной линейки, ее сравнивают с лучом света. Точно так же обстоит дело и с туго натянутой нитью, которую практически считают прямой. Чтобы убедиться, что нить хорошо натянута и не провисает, надо опять-таки взглянуть вдоль нити, т. е. (как и планку) сравнить ее с лучом света.
Значит, можно сказать, что луч света является эталоном прямой. На первый взгляд все хорошо. Но на самом деле нигде в природе не встречается то, что мы мыслим себе «одним лучом света».
Допустим, что свет небольшого источника А (рис. 2) пропускают сквозь малое отверстие. Получится узкий пучок света. Представим себе, что отверстие все время уменьшается и источник света тоже уменьшается. Тогда пучок, исходящий из отверстия, будет становиться все уже и уже. Конечно, этот пучок никогда не станет лучом, если бы даже и можно было его сделать сколь угодно узким1. Вот если бы источник света А был точкой и отверстие В тоже было точкой, тогда пучок стал бы лучом. Но ведь мы говорили о том, что в реальном мире точек не бывает. Значит, не бывает и лучей. Таким образом, и луч (т. е. прямая) является абстрактным понятием, хотя и имеет весьма реальную природу и физическое происхождение. Точно так же, как и в случае точки, рисуя на бумаге прямую, мы только создаем реальный образ - рисунок, стремясь в той или иной (нужной нам) мере сделать его похожим на те физические объекты, из которых произошло, выкристаллизовалось абстрактное понятие прямой. И здесь, как и в случае точки, абстрактное понятие прямой наделяется нами всеми свойствами, общими для тех конкретных предметов, в результате наблюдения над которыми возникло само понятие прямой.
Точно так же обстоит дело и с плоскостью. Представим себе, что свет источника А пропускают сквозь прямую щель (рис. 3). Прямизна щели может быть, например, в нужной нам мере проверена при помощи эталона - луча света так, как указано выше. Получится изображенный на рисунке пучок света. Если бы уменьшить размер источника до «идеальной» точки и сузить щель до «идеальной» прямой, тогда пучок света стал бы «идеальной» плоскостью. Здесь применимы все рассуждения, приведенные в случае прямой, и мы не будем на них останавливаться.
Да, есть и такой музей. Часов там много всяких: старинных и современных, механических и электрических, огромных и крошечных, с боем и без боя, с циферблатом и без циферблата.
Первые механические часы были изобретены около середины X в. Очень долго часы имели лишь одну стрелку - часовую. Только с 1700 г. появилась и минутная стрелка, а еще через 60 лет - секундная.
400 лет часы приводятся в действие пружиной. Но эра пружины на исходе. Современные наручные электронно-механические часы совсем и заводить не надо.
В числе тикающих и безмолвствующих обитателей музея была пара действующих часов с боем, одинаковым по тембру. Однажды они ударили подряд, как я насчитал, 19 раз. Это произошло потому, что начало боя на первых часах опаздывало по отношению ко вторым часам на две секунды. Кроме того, первые часы, оказывается, ударяли через каждые 3 секунды, а вторые - через 4 секунды. Который был час?
Решение на стр. 321.
1 В этом мысленном «идеальном» эксперименте мы умышленно не учитываем возникающие здесь физические явления: дифракцию, преломление и т. п.
312
Рис. 3. Представление о плоскости дает свет, проходящий через узкую прямолинейную щель.
Итак, в геометрии изучаются свойства абстрактных понятий - точки, прямой, плоскости. Эти свойства формулируются и доказываются в так называемых теоремах. Доказательство же всех теорем основано в конечном счете на некоторых аксиомах, которые в геометрии никак не доказываются. Подробнее о том, как выбираются аксиомы, каким требованиям должен удовлетворять этот выбор, рассказано в статье «Как возникла геометрия».
Наиболее ранняя из дошедших до нас систем аксиом была построена Евклидом (III в. до н. э.). Аксиоматика (система аксиом), данная Евклидом, была, правда, далеко не безупречной. Строгое современное изложение евклидовой геометрии было дано лишь в конце XIX в. и базируется на двух десятках аксиом, которые мы здесь перечислять не будем. Все теоремы геометрии лишь с той точностью описывают
реальный мир, с какой аксиомы правильно отражают действительное положение вещей.
Существо дела заключается в следующем. Пусть, например, мы рассматриваем распространение света в природе - так сказать, «световые лучи». Они ведут себя в соответствии с действующими физическими законами. И вот геометры-математики выбирают некоторые обнаруженные в опытах особенности распространения света и объявляют их аксиомами, присущими абстрактным понятиям точки, прямой, плоскости. На базе выбранных аксиом и строят математическую науку - геометрию. Эта геометрия является как бы мысленным слепком с действительного мира. Изучение этого слепка позволяет обнаруживать закономерности реального мира уже не путем непосредственных измерений, а мысленно, геометрически (т. е. на слепке).
Чтобы подробнее пояснить это, рассмотрим, например, задачу об определении расстояния между пунктами А и В, разделенными рекой (рис. 4). Понятно, что прямое измерение расстояния АВ практически неосуществимо. (Еще труднее найти расстояние между звездами.) Для решения подобных задач необходима геометрия. Как же найти расстояние АВ с помощью геометрии? Укажем два способа решения этой задачи.
Первый способ. Выберем на местности еще один пункт С так, чтобы расстояние А С можно было непосредственно измерить. Найдя АС, измерим с помощью какого-либо угломерного инструмента (скажем, теодолита) поочередно углы a и g (положим для определенности, что они оказались острыми).
Рис. 4. Измерение расстояния между пунктами А и В, разделенными рекой.
313
Теперь, уже мысленно, рассмотрим абстрактный треугольник А B С, у которого задана сторона А С и углы a и g. Мы можем для наглядности нарисовать этот треугольник (рис. 5), хотя никакой необходимости в этом нет, все дальнейшие рассуждения можно проводить мысленно, не обращаясь к рисунку. Поэтому и рисунок, если уж его желательно сделать, может быть выполнен приблизительно, без соблюдения каких-либо чертежных правил.
Опуская из вершины В перпендикуляр на сторону А С, получим точку D. Обозначим BD = h, AD=x. Тогда DC=AC-x. Очевидно,
h/x = tg a ; h/(A C-x)=tg g. Отсюда
xtg a =(AC-x)tg g . Следовательно:
AC tg g /(tg a +tg g).
После этого по теореме Пифагора легко найдем:
АВ= √‾(x² + h²)= √‾( x² + (xtg a))² = х √‾ (1+ tg² a) =( AC tg g √‾(1+tg² a))/(tg a +tg g).. Зная АС, a, g, можно по полученной формуле легко найти искомое расстояние АВ 1 .
Второй способ. Постараемся на бумаге по возможности точно начертить план местности (план треугольника А B С). Разумеется, невозможно начертить его в натуральную величину. Поэтому выберем определенный масштаб и уменьшим измеренную величину АС в n раз. Построим на чертеже отрезок
А'С'=(1/ n) АС (рис. 6). Далее, на концах этого отрезка с помощью транспортира построим углы а и у, равные найденным при измерении на местности. Продолжив стороны этих углов, получим точку В' - третью вершину треугольника.
Так как два угла а и у треугольника А'В'С' равны соответствующим углам треугольника А B С, то эти треугольники подобны. А так как подобие треугольников означает пропорциональность их соответствующих сторон, то приходим к выводу, что сторона А'В' должна быть меньше стороны АВ также в n раз. Поэтому, измерив на чертеже А'В', можно найти, что АВ = n А'В'.
В первом случае мы нашли АВ простым вычислением, во втором - пришлось дополнительно измерить на чертеже А'В' и выполнить достаточно точный чертеж. В обоих случаях для определения АВ нам пришлось воспользоваться многими теоремами геометрии: теоремой Пифагора, теоремой о свойстве подобных треугольников и т. п. Отметим, что второй способ (наряду с первым) часто используется в инженерной практике, где поэтому весьма важным является точное выполнение чертежей. Можно ли гарантировать, что описанные методы дают величину АВ, которая с необходимой точностью совпадает с расстоянием между пунктами А и В, если бы его действительно уда-
¹ Расстояние АВ можно найти еще проще, если воспользоваться известной в тригонометрии теоремой синусов.
314
лось измерить? Ответ на этот вопрос зависит от того, насколько точно аксиомы геометрии (а следовательно, теоремы) отображают реальную действительность, насколько хорош наш геометрический слепок с реального мира.
Разумеется, может оказаться, что этот слепок недостаточно хорош. Тогда надо попытаться сделать лучший. Для этого надо тщательнее проанализировать опыты, на основании которых выбраны те или иные аксиомы, точнее, выбрать аксиомы. С помощью новых аксиом, более точно отображающих действительность, надо построить новую геометрию, новый, более точный слепок с реального мира.
В течение двух тысячелетий считалось, что евклидова геометрия описывает мир с беспредельной точностью, что евклидов слепок с реального мира идеален. Эта точка зрения была впервые поколеблена лишь в 1826 г. русским математиком Н. И. Лобачевским. Чтобы разъяснить его идеи, остановимся подробно на анализе одной из самых интересных аксиом евклидовой геометрии.
Выбрав систему аксиом, начинают доказывать теоремы все более и более сложные.
Весьма просто, например, с помощью теоремы о внешнем угле треугольника доказывается такая теорема:
Две прямые, перпендикулярные третьей прямой, не пересекаются.
Дадим теперь следующее определение:
Две прямые, лежащие в одной плоскости и не пересекающиеся, называются параллельными.
Пусть теперь на плоскости даны прямая а и точка А (рис. 7). Ясно, что через точку А можно провести прямую b , параллельную а. Для этого достаточно опустить из точки А перпендикуляр А В на прямую я, а затем из
точки А провести прямую b , перпендикулярную АВ. Это и будет искомая параллельная. Итак, параллельные прямые существуют!
Теперь возникает вопрос: нельзя ли через точку А провести еще одну прямую b ', также параллельную прямой а? (Напомним, что все происходит на одной плоскости, т. е. мы занимаемся только планиметрией.) Тому, кто не думал над этим раньше, не изучал этого вопроса, хочется немедленно и категорически ответить: нет, нельзя! - прямая b ' пересечет прямую а, возможно, очень далеко, но непременно пересечет!
Воздержимся пока от столь категорического ответа и постараемся вдуматься в поставленный вопрос глубже.
Возьмем на прямой а точку С и соединим ее с точкой А прямой с. Теперь будем передвигать точку С вправо по прямой а. При этом прямая с будет поворачиваться около точки А. Ясно, что прямая с никогда не сольется с прямой b , ибо b с а не пересекается. Но прямая с, поворачиваясь в одном и том же направлении, будет неограниченно приближаться к какому-то определенному предельному положению, когда точка С неограниченно удаляется вправо. Теперь спросим себя: будет ли прямая b той предельной прямой, к которой неограниченно приближается прямая с? Или, может быть, прямая с будет неограниченно приближаться к предельной прямой b' , отличной от b , так что прямая с, поворачиваясь, не сможет войти внутрь угла а. Опять хочется отвергнуть это предположение.
Однако подумаем еще. Проведем из точки А луч а под углом j <90° к прямой АВ. Если этот угол j мал, прямые а и d пересекутся на чертеже. Надо только продлить луч d. Если же теперь увеличить угол j (см. рис. 7), прямые а и d пересекутся уже не на чертеже, а где-то за полем книги. Еще немного увеличим угол j. Тогда при продолжении прямые a и d будут пересекаться дальше, скажем, на расстоянии нескольких сот метров. Ясно, что практически убедиться в этом весьма трудно, почти невозможно, но принципиально мыслимо.
Теперь еще увеличим угол j. Пусть он отличается от 90°, допустим, на одну миллионную долю градуса. Что же теперь можно сказать о пересечении прямых а и d? Хочется опять их мысленно продолжить. Но так ли хорошо мыслим мы это продолжение? Не теряет ли смысл этот мысленный эксперимент? Ведь если угол j достаточно близок к 90°, то продолжать прямые придется туда, куда не удалось загля-
315
дывать даже при помощи самых мощных телескопов.
Напомним, что аксиомы изучаемой сейчас геометрии должны отражать свойства световых лучей и подвергаться многократной проверке на опытах со световыми лучами.
Наше предположение о том, что лучи а и d пересекутся, основано действительно на большом практическом опыте. Говоря, что лучи a и d пересекутся даже очень далеко (например, на расстоянии 100 млн.км), мы базируемся на большом опыте астрономических наблюдений.
Предположение же о том, что лучи света a и d пересекутся за пределами видимости самых мощных телескопов, уже основано на чистой фантазии. Ведь неизвестно, как там поведут себя лучи света. Здесь уже нет никаких оснований ссылаться на эксперимент.
Мы договорились, что эталон прямизны - это луч света. Чтобы сделать какое-либо заключение о поведении прямых a и d, надо знать физические свойства световых лучей.
Итак, вопрос о том, можно ли через точку А провести две прямые b и b ', параллельные а, зависит от свойств световых лучей. Ясно, что, если угол j очень близок к 90°, экспериментальная проверка того, пересекутся ли лучи а и d, невозможна.
Следует хорошо уяснить, что вопрос о том, можно ли из точки А провести только одну прямую, не пересекающую прямую а, решается не так уж просто. Ничего категорически здесь сразу сказать нельзя.
Разумеется, неочевидность какого-либо утверждения ни в какой мере не означает его несправедливости. Ведь теорема Пифагора, например, тоже не так уж очевидна: совсем не сразу можно поверить в то, что площадь квадрата, построенного на гипотенузе любого прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах. Чтобы убедиться в справедливости теоремы Пифагора для любого прямоугольного треугольника, ее доказывают. Доказательство это опять-таки основывается на тех же аксиомах.
Возможно, в нашем вопросе положение аналогично. Иными словами, можно ли доказать, исходя из принятых аксиом, такое предложение :
(А) Через точку вне прямой нельзя, провести более одной прямой, параллельной данной.
Возможно, что еще Евклид задавался этим вопросом, однако ответа на него у Евклида нет. Но так как этим предложением (или эквивалентным ему) приходилось пользоваться при доказательстве других теорем, пришлось принять предложение (А) за аксиому1. В стабильном учебнике предложение (А) названо аксиомой о параллельных. Итак, принимают новую аксиому, хотя, как объяснялось выше, есть все основания усомниться в ее справедливости в мире световых лучей.
Оставим пока в стороне вопрос о том, включать ли аксиому (А) в число аксиом геометрии, предназначенной для описания мира световых лучей. Укажем лишь, что именно с помощью аксиомы (А) в школьном учебнике доказывается теорема:
(В) Сумма внутренних углов любого треугольника равна 180° (в радианной мере p).
Несколько сложнее доказывается обратная теорема:
Если сумма внутренних углов хотя бы одного треугольника в точности равна 180°, то справедлива аксиома о параллельных, т. е. через точку А невозможно провести в плоскости две различные прямые, не пересекающие данную прямую а, которая лежит в той же плоскости.
Таким образом, из аксиомы о параллельных следует, что сумма внутренних углов любого треугольника равна 180°; наоборот, из того, что сумма углов некоторого треугольника равна 180°, следует аксиома (А).
Значит, в списке аксиом евклидовой геометрии можно вычеркнуть аксиому о параллельных, но вместо нее внести предложение (В). При этом все остальные теоремы евклидовой геометрии остались бы неизменными.
Мы выше пояснили трудность (даже практическую невозможность) проверки аксиомы о параллельных в мире световых лучей. Если бы даже можно было выделить сколь угодно тонкий пучок световых лучей и если бы не было никакого их поглощения, то и тогда совершенно непонятным оставалось бы их поведение за пределами видимости современных телескопов. Всегда неясным оставался бы вопрос о том, пересекутся ли лучи а и b ', если угол j близок к 90 (см. рис. 7). Сказать, что лучи будут и дальше идти по прямой,- значит вообще ничего не сказать, ибо свойства прямой,
¹ Евклид в качестве аксиомы принял другое предложение, которое, однако, равносильно предложению (А)
316
которые кладутся в основу рассматриваемой сейчас нами геометрии, выводятся на основании изучения свойств реального мира световых лучей, а не наоборот.
Приняв аксиому (А), мы получим геометрию, в которой сумма углов любого треугольника равна 180°. Приняв предложение, противоположное аксиоме (А), мы получим геометрию, в которой сумма углов всякого треугольника отлична от 180°. Как же здесь быть? Принимать или не принимать аксиому (А)?
Ввиду чрезвычайных трудностей, связанных с экспериментальной проверкой аксиомы (А) в опытах со световыми лучами, возникает вопрос о том, не проще ли на таких опытах проверять предложение (В).
Поясним подробнее возникающее здесь положение.
Представим себе, что на местности (рис. 4) ведутся геодезические работы. Пусть в пункте В на штативе укреплен шарик, который геодезист наблюдает в обычный теодолит, установленный в пункте А.
Какой же величины надо взять шарик в пункте В для этих наблюдений? Шарик надо выбрать так, чтобы его изображение получилось с возможной точностью в центре окуляра теодолита. Если шарик таков, что его изображение будет большим кружком, его надо уменьшить для более точной наводки. Значит, шарик не должен быть слишком большим. Уменьшать шарик, однако, имеет смысл лишь до тех пор. пока это уменьшение сказывается на точности наводки теодолита. Если чувствительность прибора не даст возможности улучшить наводку путем дальнейшего уменьшения шарика, такое уменьшение просто бесполезно. Выбрав шарик надлежащего размера, геодезист считает, что он имеет дело с «точками» А и В, соединенными отрезком АВ. При этом, как и выше, шарик В может на самом деле быть довольно большим (это зависит, разумеется, от расстояния АВ).
Теперь представим себе, что в пункте С также установлен на штативе шарик надлежащих размеров. Поочередно наводя теодолит на шарики В и С, геодезист находит величину ·а, равную разности отсчетов на лимбе теодолита.
Как указывалось выше, геометрия оперирует абстрактными понятиями точки, прямой, треугольника и т. д. Поэтому наш геодезист, выполнив вполне конкретный физический эксперимент с шариками и снопиками световых лучей, рассматривает абстрактный треугольник А B С и считает, что величина угла в вер-
шине А равна a - разности отсчетов на лимбе теодолита.
Понятно, что величина a зависит от того, насколько хорошим и совершенным был примененный теодолит. Поэтому, применяя различные измерительные приборы, геодезист должен был бы каждый раз изучать другой абстрактный треугольник А B С.
Представим себе для определенности, что конструкция теодолита не дает возможности фиксировать показания на лимбе более мелкие, нежели 10'. В таком случае, выполнив отсчет на лимбе после наведения на шарик B, говорят, что отсчет сделан с точностью до 10'. То же самое относится и к наводке теодолита на шарик С.
Найдя разность отсчетов a, геодезист считает, что, применив другой, более точный теодолит, он мог бы получить другую разность, однако ее отличие от a не превысит 20'.
Таким образом, рассматривая абстрактный треугольник А B С с углом A, равным a, геодезист вправе считать, что, применяя более точные приборы, он мог бы получить для угла a другую величину, лежащую в пределах от a - 20' до a +20'.
Аналогично можно для углов В и С получить величины b и g и найти сумму s = a + b + g .
Возникает вопрос: равна ли эта сумма 180°? Понятно, что такое совпадение маловероятно. Вспомним прежде всего, что каждая наводка теодолита выполнялась с точностью до 10'. Для определения а теодолит пришлось наводить 6 раз. Поэтому применение более точного прибора могло бы привести к получению другой суммы, находящейся в промежутке от s - 1° до s +1°.
Итак, определение суммы углов рассматриваемого абстрактного треугольника зависит от точности проведенных измерений (в данном случае от точности примененного теодолита). В нашем случае геодезист вправе рассмотреть абстрактный треугольник, сумма углов которого отличается от найденной при измерении величины о, но не более чем на 1°.
Здесь возникает другой вопрос. Насколько измеренная сумма углов о отличается от 180°? Превосходит ли это отличие 1°? Находится ли разность между 180° и а в пределах точности примененных инструментов? Иными словами, может ли геодезист в данном случае рассматривать абстрактный треугольник с суммой углов 180°?
Проанализируем возможные результаты измерения. Здесь имеются две возможности.
317
1. В результате измерения получилась сумма s = a + b + g, отличие которой от 180° превосходит точность проведенных измерений (в данном случае 1°). В этом случае геодезист должен рассуждать примерно так. Если принять аксиому (А), в нашей геометрии сумма углов всякого треугольника будет равна 180°. Проведенный же опыт показывает, что принятая точность измерений не согласуется с таким выводом. Это означает, что такая геометрия для нашего геодезиста недостаточно хороша. Выводы ее он не смог бы применять в своей практике.
Зная длину АС, углы a и g, он не смог бы с необходимой точностью, как это описано выше, определить длину АВ, ибо теорема Пифагора и признаки подобия треугольников справедливы лишь там, где сумма углов треугольника равна 180°. Ему пришлось бы для практических потребностей строить геометрию, где аксиома (А) не справедлива и, следовательно, сумма углов треугольника не равна 180°.
2. Сумма углов s = a + b + g, полученная в результате измерения, отличается от 180° на величину, не превосходящую точность измерений (в данном случае 1°). В этом случае геодезисту для практических нужд вполне пригодна геометрия, в которой сумма углов треугольника равна 180°. У него нет никаких оснований отвергать аксиому (А), а равно и предложение (В). Обычная евклидова «школьная» геометрия здесь оказывается весьма полезной, ее выводы приобретают большое практическое значение с точностью, принятой в измерениях нашего геодезиста.
Однако необходимо заметить, что геодезист и в данном случае не должен слишком пренебрежительно относиться к геометрии, где неверна аксиома (А) и где сумма углов треугольника отлична от 180°. Не исключена возможность, что и такая геометрия в будущем окажется ему полезной. Если все измерения геодезиста пока хорошо согласовывались с той геометрией, где сумма углов треугольника равна 180°, то, может быть, в дальнейшем, увеличив точность приборов или измеряя углы значительно больших космических треугольников, он столкнется с тем, что при новых измерениях обычная геометрия уже не будет описывать мир с достаточной точностью. И тогда понадобится совсем другая геометрия.
Итак, вопрос заключается лишь в том, какая геометрия с большей точностью описывает мир световых лучей, какой мысленный слепок с реального мира является более точным.
Вполне владея изложенными идеями, Н. И. Лобачевский уже в первой половине XIX в. имевшимися в то время астрономическими средствами измерил сумму углов весьма большого космического треугольника. За вершины были взяты две самые удаленные точки на эллиптической орбите Земли и одна из далеких звезд. В результате измерения получилась величина, как и следовало ожидать, отличная от 180°, однако это отличие не выходило за пределы точности примененных инструментов. Таким образом, вопрос о том, какая геометрия точнее описывает мир световых лучей, остался открытым. Было неясно, понадобится ли вообще когда-нибудь геометрия, в которой не имеет места аксиома (А). Не является ли такая геометрия бесполезным плодом фантазии?
Выше пояснялась естественность построения геометрии, в которой сумма внутренних углов треугольника не равна 180° и, следовательно, не имеет места утверждение (А).
Впервые такую геометрию построил и развил Н. И. Лобачевский в 1826 г. Геометрия Лобачевского строится на тех же аксиомах, что и евклидова, за исключением аксиомы о параллельных, которая заменяется противоположным утверждением - аксиомой Лобачевского:
Через точку вне прямой в данной плоскости можно провести по крайней мере две прямые, не пересекающие данную прямую.
Мы видели, что вопрос о том, какая геометрия - Евклида или Лобачевского - точнее описывает мир световых лучей, решается не так уж просто, хотя аксиома Лобачевского и кажется на первый взгляд парадоксальной. Огромной заслугой Лобачевского было то, что он этот вопрос поставил.
Впоследствии было построено много других геометрий - других мысленных слепков с реального мира. Вопрос же о том, действительно ли понадобится какая-либо из этих геометрий при изучении реального мира световых лучей, оставался по существу открытым вплоть до 1916 г., когда крупнейший физик А. Эйнштейн создал так называемую общую теорию относительности.
Широко известен анекдот о том, что Ньютон открыл закон тяготения, наблюдая за падением яблока. Насколько же точно ньютонов-
318
ский закон отображает реальное положение вещей? Нельзя ли с помощью очень точных инструментов обнаружить, что притяжение тел может отклоняться (пусть очень мало) от закона Ньютона? Здесь можно поставить те же вопросы, какими мы занимались при разборе евклидовой аксиомы о параллельных.
Дело в том, что ньютоновские законы также представляют собой некоторый абстрактный, мысленный слепок с реального мира. Это как бы физический слепок, в то время как евклидова аксиоматика является геометрическим слепком.
Подобно этому и законы электрического взаимодействия (например, закон Кулона) также являются определенным физическим слепком с реального мира.
Вплоть до создания общей теории относительности считалось твердо установленным, что реальный мир представляет собой нечто подобное бесконечной пустой «евклидовой комнате», в которой, словно мебель, расположены реальные тела, предметы, взаимодействующие друг с другом. Казалось совершенно несомненным, что свойства этой «евклидовой комнаты» никак не связаны с перемещением и взаимодействием находящейся в ней мебели.
Законы же перемещения и взаимодействия материи в этой пустоте описывались в физических теориях-слепках. Однако считалось, что эти теории могут делаться независимо от того, как сделан геометрический слепок. Кроме того, ньютонов слепок считался столь же бесконечно совершенным и точным, как и евклидов геометрический слепок.
Опыты, однако, показали, что известные физические теории столь же несовершенны, как и евклидова геометрия.
Чтобы несколько разъяснить это, расскажем об одном эксперименте, который уже неоднократно повторялся астрономами и показал хорошее ' совпадение с заранее полученными выводами теории относительности.
Представим себе на Земле наблюдателя, который, находясь в определенный момент в точке О1 (рис. 8), видит звезду А и вблизи от нее Солнце S 1. Наблюдение проводится в небольшой промежуток времени, так что звезду и Солнце можно считать неподвижными, а траекторию Земли - прямолинейной: Если Земля движется по своей орбите с известной скоро-
стью в направлении от О1 к O2, то, пользуясь теоремами евклидовой геометрии, нетрудно определить, в какой момент времени Солнце заслонит от наблюдателя звезду А. Это должно произойти тогда, когда Земля переместится в точку O2 (рис. 8).
Эксперимент, однако, показывает, что в действительности звезда А закрывается Солнцем с некоторым опозданием, величина которого хорошо согласуется с предсказаниями теории относительности.
Как же объясняется это явление? Оказывается, сильное поле тяготения, создаваемое Солнцем, заставляет лучи света, проходящие вблизи Солнца, вести себя не так, как того требует евклидова геометрия. А именно, лучи как бы искривляются, и получается картина, схематически изображенная на рис. 9. Находясь в точке О2, наблюдатель видит звезду. Лишь когда наблюдатель переместится в точку O3, Солнце закроет от него звезду А.
Можно попытаться объяснить обнаруженное отклонение, оставаясь в рамках евклидовой геометрии и ньютоновской теории тяготения. Именно, зная массу Солнца и массу движущегося фотона (кванта света), можно на основании
¹ Заметим, что такие опыты производятся при полном солнечном затмении, когда диск Солнца закрывается от наблюдателя диском Луны.
319
ньютоновского закона тяготения вычислить отклонение фотона от евклидовой прямой. Опыт, однако, показывает, что действительное отклонение оказывается примерно вдвое большим того отклонения, которое вычислено указанным путем.
В таком случае приходится предположить, что евклидова геометрия или ньютоновская теория тяготения (или обе они) являются недостаточно точными слепками действительного мира, ибо не позволяют объяснить наблюдаемые явления. Общая теория относительности как раз и дала новый, более точный слепок. В соответствии с этой теорией поведение световых лучей вовсе не обязано следовать законам евклидовой геометрии. Геометрия, пригодная для описания поведения световых лучей, должна целиком и полностью определяться распределением и состоянием материи в мире. Каждое перемещение массы и изменение энергии вещества влечет изменение структуры всего физического пространства, а следовательно, и необходимость выбора более подходящего, неевклидова геометрического слепка.
Нельзя считать, что световые лучи в окрестности Солнца (рис. 9) перестали быть прямыми, что они искривлены. Они, так же как и лучи, проходящие вдали от Солнца, являются идеальными прямыми, однако поведение этих прямых должно описываться не евклидовой системой аксиом, не евклидовой геометрией, а некоторой другой геометрией.
Так как распределение и состояние материи в реальном пространстве изменяется во времени, то и геометрия, описывающая наше реальное пространство с достаточной точностью, тоже не остается неизменной, а изменяется со временем. Значит, в формулировке аксиом геометрии должно участвовать время. Понятия пространства и времени оказываются неотделимыми, неразрывными.
Теория относительности Эйнштейна объединила в одно целое изучение физических и геометрических свойств реального мира. Она как бы дала единый физико-геометрический слепок нашего мира.
Оказалось, что мир нельзя рассматривать как пустое евклидово пространство, заполненное материей. Каждое изменение поля тяготения, всякое перемещение массы и изменение энергии вещества влечет изменение структуры всего физического пространства, а следовательно, и необходимость выбора более подходящего геометрического слепка.
В соответствии с теорией Эйнштейна выбор подходящей геометрии целиком и полностью определяется распределением и состоянием материи в реальном мире.
Для того чтобы иметь возможность подбирать в каждом случае подходящую геометрию, целесообразно заранее иметь целый набор, как бы библиотеку таких мыслимых слепков. В настоящее время математиками разработаны методы построения бесконечного числа таких геометрий.
Различные геометрические пространства, т. е. различные мыслимые геометрические слепки, различают по тому, насколько они отличаются от евклидова. Само это отличие называют кривизной. Кривизна геометрического пространства определяется некоторыми числами, которые характеризуют величину отличия той или иной геометрии от евклидовой. Каждая «кривая» геометрия основывается, по существу, на некоторых аксиомах. Совокупность аксиом такой геометрии отличается от евклидовой системы аксиом. Имеется один интересный и простой признак, которым можно характеризовать отличие геометрии от евклидовой, не перечисляя всех аксиом. Этим признаком является как раз теорема о сумме углов треугольника. В евклидовой геометрии она всегда равна 180°. В других геометриях это не так. Там сумма углов треугольника может быть больше или меньше 180°, в зависимости от размеров и расположения треугольника в пространстве.
Если обозначить сумму углов треугольника через а, то можно считать, что величина кривизны характеризуется отношением величины s - 180° к площади треугольника. Величина а - 180° в различных геометриях может иметь знак плюс или минус. В соответствии с этим говорят, что пространство имеет положительную или отрицательную кривизну.
В евклидовой геометрии s - 180°=0; поэтому говорят, что евклидово геометрическое пространство имеет нулевую кривизну.
Выше было показано, что, развивая технику измерений, совершенствуя свои знания реального мира, мы неизбежно приходим к необходимости построения геометрии, отличной от евклидовой. Однако евклидова геометрия во многих вопросах является отличным орудием практики, инженерной техники и т. п. Смешон был
320
бы, например, инженер, который стал бы учитывать, что две вертикальные линии отвеса не параллельны, а пересекаются в центре Земли. Еще меньше оснований у инженера предполагать, что в построенном треугольнике сумма углов отлична от двух прямых.
Евклидова геометрия в таких вопросах с большой точностью описывает реальный мир световых лучей, и не случайно изучение свойств пространства люди начали именно с евклидовой геометрии.
Все это, разумеется, ни в какой мере не умаляет важности неевклидовых геометрий. Они находят себе применение в важнейших теоретических и практических вопросах современной физики и математики.
Первая неевклидова геометрия была построена Лобачевским. Многовековая привычка к понятиям евклидовой геометрии не дала возможности даже крупным математикам, современникам Лобачевского, понять его идеи. Триумф этих идей наступил позднее. Теперь
они прочно вошли в науку о природе и хорошо известны каждому физику и математику.
Геометрические понятия тесно связаны с физическими явлениями, происходящими в реальном мире. При этом следует иметь в виду, что геометрия применима не только к изучению явлений, связанных с распространением света. Можно рассмотреть и какие-нибудь другие реальные объекты, не имеющие никакого отношения к распространению света. Некоторые из них можно принять за эталон прямизны, подобно тому как это делалось с узкими снопиками световых лучей. Изучая эти объекты, можно подобрать аксиомы и построить соответствующую геометрию. Можно, например, в качестве эталона прямизны принять траектории твердых тел достаточно малого размера, движущихся по инерции, т. е. при отсутствии воздействия на них внешних сил. Полученная при этом геометрия (как и геометрия, построенная для изучения световых лучей) будет лишь в первом приближении совпадать с евклидовой.
Ответы и решения
Ответ к стр. 290. Вот все двузначные «самородки»: 20, 31, 42, 53, 64, 75, 86, 97.
Ответ к стр. 291.
Ответы к стр. 303.
1
Треугольники равновелики, так как каждый составлен из пары треугольников (3, 4, 5).
Решение к стр. 312. Построим ряд параллельных отрезков, промежутки между которыми будем считать изображением секунд. Точками изобразим удары боя первых (А) и вторых (В) часов соответственно условию задачи (см. рис.).
Схема показывает, что под номерами 5, 11, 17 удары происходят
Наименьшая возможная площадь у трех равновеликих прямоугольных треугольников 840. Стороны: (40, 42, 58), (24, 70, 74), (15, 112, 113).
одновременно и на слух сливаются каждый раз в один удар. Максимальное число ударов для каждых часов в отдельности равно 12, но если бы это было так, то мы насчитали бы 21 удар. На схеме изображены 19 ударов, что соответствует одиннадцати раздельным ударам часов А и В. Значит, часы показывали 11.
Ответ к стр. 307. Куб имеет 11 разверток различных форм. Из них в шести формах четыре грани куба развертываются в одну полоску; в четырех формах не более трех граней в полоске; в одной - не более двух граней в полоске.
Ответ к стр. 309. Невозможно. Каждый кубик имеет 6 граней. Для получения кубика, расположенного в центре данного куба, должны быть выпилены полностью все шесть граней (у остальных кубиков имеются уже готовые грани). Как ни перекладывай части данного куба, а одним плоским разрезом не получишь более одной грани кубика.
321
УРАВНЕНИЯ И ФУНКЦИИ
Сохранились два замечательных письменных памятника математики египетского народа, каждому из которых около 4 тыс. лет. Первый из них находится в Москве, в Музее изобразительных искусств имени А. С. Пушкина, и называется Московским папирусом. Он составлен около 1900 лет до н. э. Другой памятник, больший по объему, составленный лет на 200 позднее Московского, хранится в Лондоне и
имеет заглавие: «Наставление, как достигнуть знания всех темных [трудных] вещей... всех тайн, которые скрывают в себе вещи... Писец [чиновник] Ахмес написал это... со старых рукописей...» Это сборник 85 задач с решениями. Его называют папирусом Ахмеса (иногда папирусом Райнда по имени английского коллекционера, который приобрел этот документ около ста лет назад).
В папирусе Ахмеса наряду с различными другими содержится ряд задач, которые мы решаем при помощи уравнений первой степени.
322
Египетский автор решает их способом, который затем в течение нескольких тысячелетий употреблялся разными народами для решения подобных задач и называется методом ложного положения.
Это есть тот же метод предположений, который на уроках арифметики применяется и в наше время.
Египтяне за 2000 лет до н. э. имели для обозначения неизвестного числа особый символ и название (последнее произносится «хау» или «аха» и условно переводится словом «куча»).
Вот одна из задач папируса Ахмеса: «Куча. Ее седьмая часть, ее целое. Что составляет 19». Это значит: требуется найти число, которое, будучи сложенным с его седьмой частью, даст в сумме 19. Иными словами, требуется решить уравнение
x+x/7 =19.
На рис. 1 представлено в виде таблицы египетское решение задачи. Смысл этого решения таков. Предположим, что «куча» есть 7; тогда
1/7 будет 1 (см. первый столбец). Звездочки означают, что эти числа использованы при решении. При сделанном предположении правая часть решаемого уравнения равнялась бы восьми (7+1), поэтому во втором столбце стоит число 8. Оно меньше требуемого задачей числа 19. Автор в уме удваивает его и получает 16. Дальнейшее удваивание дало бы 32, но это превышает требуемое задачей число 19, и в решении отмечается поэтому звездочкой число 16 как долженствующее войти в искомое решение. Не хватает еще 19-16 = 3. Автор пробует взять
1/2 от 8, т. е. 4. Эта доля предположенного числа не может войти в искомое решение, так как надо добавить лишь 3. Тогда решающий берет 1/4 и 1/8 от 8, т. е. 2 и 1, отмечает их как составляющее вместе с 16 число 19.
Таким образом, автор установил (второй столбец решения), что первоначально предположенное значение для «кучи» надо взять
2+1/4+1/8 раз, чтобы удовлетворить условию
11
задачи. Остается 7 умножить на 2 +1/4+1/8 (египтяне, как и многие другие народы, знак «плюс» при сложении не ставили; мы также в смешанных числах пишем 31/4 вместо 3+1/4). Автор ре-
шения вместо умножения 7 на 21/4 1/8 умножает
21/41/8 на 7. Для этого в третьем столбце он записывает число 21/41/8, затем удвоенное (..) и
учетверенное (....) значения его. Эти три числа
складываются, и получается для «кучи» значение
161/2 1/8, К нему прибавляется 1/7 «кучи», т. е.
21/4 1/8, и это дает в результате 19. Последняя
часть решения представляет проверку его и во многих задачах отмечается словами: «будет хорошо».
В дальнейшем у разных народов был создан метод двух ложных положений, применявшийся еще в XVIII в. Мы находим применение его и в напечатанной в 1703 г. «Арифметике» Л. Ф. Магницкого, которая является первым на русском языке учебником всех разделов школьной математики (арифметики, алгебры, отчасти геометрии и тригонометрии). Вот пример решения Магницким задачи по способу двух ложных положений.
323
Решение задачи методом двух ложных положений.
Задача. Отец ученика спросил учителя, сколько у того учится ребят. Учитель ответил, что если бы у него было учеников еще столько, сколько сейчас есть, и полстолька, и четверть столька, и сын спрашивающего, то их было бы ровно 100 человек.
В нашей записи задача сводится к решению уравнения:
x + x + x /2+ x /4+1=100 .
Решение по Магницкому. Делаем первое предположение: учеников было 24. Тогда согласно условию имели бы: 24+24+12+6+1 = 67, т. е. на 100-67=33 меньше требуемого (первое отклонение).
Делаем второе предположение: учеников было 32, тогда 32+32+16+8+1=89, т. е. на 100-89=11 меньше требуемого (второе отклонение). На основании веками выработанного правила Магницкий указывает готовый способ нахождения х :
(32·33-24·11)/(33-11)=36.
Способ этот заключается в правиле: «Множить первое предположение на второе отклонение и второе предположение на первое отклонение, из большего произведения вычесть меньшее и разность разделить на разность отклонений».
Так же надо поступить в том случае, если при обоих предположениях получилось больше, чем требуется в задаче.
Если при одном предположении получится больше, а при другом - меньше, чем требует условие задачи, то в формуле, по которой вычисляется х, вместо знака «-» надо поставить знак «+». Например, пусть первое предположение 60; тогда: 60+60+30+15+1 = 166, 166-100 = 66 (избыток). Пусть второе предположение 20; тогда 20+20+10+5+1=56, 100-56 = 44 (недостаток). В таком случае1
x=( 60·44 + 20·66)/(66+44)=36
Важным этапом в развитии учения об уравнениях является введение понятия неизвестного числа и символа для его обозначения. Это - «куча» с особым символом для ее обозначения у египтян и соответственно другие названия и обозначения у вавилонян, древних греков, индийцев, народов Средней Азии. У европейских народов систематическое обозначение неизвестного числа разными знаками возникает в средние века. Употребление для этого букв х, у, z окончательно устанавливается в XVII в. в работах Р. Декарта.
Способ решения уравнений первой степени, основывающийся на свойствах арифметических действий, развивался у разных народов в течение ряда веков. Основными приемами при этом были: перенос членов уравнения из одной части равенства в другую с противоположным знаком и приведение (соединение) подобных членов. Первый из этих приемов мог привести к понятию отрицательного числа, которое возникло значительно позже той эпохи, когда человек стал решать задачи, приводящиеся к уравнению первой степени. Вследствие этого уравнению придавали такой вид, чтобы все его члены были положительными, и давали специальные правила для разных видов уравнений с положительными членами. Среднеазиатский математик ал-Хорезми в IX в. ясно понимал, что решение уравнения первой степени сводится к указанным двум операциям: к переносу отдельных членов его из одной части ра-
¹ Правило, применяемое для вычисления х, легко обосновать (см.: И. Я. Депман. Рассказы о математике. М., Детгиз, 1954, стр. 61-62).
324
венства в другую (аль-джебр) и приведению подобных членов (аль-мукабала). Слово «аль-джебр» означало «восстановление»: при переносе вычитаемого числа (отрицательного члена) из одной части уравнения в другую оно превращается в положительное, т. е. восстанавливается, число. Название «аль-джебр» (aljebr) превратилось в слово «алгебра», употребляемое всеми народами.
Некий математик старого времени выразил правила аль-джебр и аль-мукабала стихами, которые в русском переводе звучат так:
Аль-джебр
При решеньи уравненья,
Если в части одной,
Безразлично какой,
Встретится член отрицательный;
Мы к обеим частям
Равный член придадим,
Только с знаком другим,
И найдем результат положительный.
Аль-мукабала
Дальше смотри, в уравненье
Можно ль сделать приведенье;
Если члены есть подобны,
Соединить их удобно.
Ал-Хорезми широко применял уравнения для решения практических задач «различного рода и сорта» (общим приемом), что привело к установлению у европейских ученых взгляда на начальную алгебру как на общую, или универсальную, арифметику (И. Ньютон - в XVII в ., Л. Эйлер - в XVIII в.). Для начальной алгебры, изучаемой в школе, этот взгляд остается в силе и в наше время.
Из древнегреческих математиков способами решения уравнений первой степени, сходными с нашими правилами, по-видимому, владел Диофант (III в. н. э.), но часть его книги о решении уравнений первой степени до нас не дошла. Способы записи уравнений и обозначения, для нас кажущиеся естественными и простыми, окончательно выработались лишь в XVII в. (Ф. Виет, Т. Гарриот, Р. Декарт) и вошли во всеобщее употребление только в XVIII в. под влиянием многочисленных работ Л. Эйлера.
Способы решения систем уравнений первой степени появляются сначала в Индии, Китае, у народов Средней Азии и Ближнего Востока ив Европе с XIII в. (Леонардо Пизанский - XIII в., Лука Пачоли - XV в., Михаил Шти-
Совершенные числа
Число 6 делится на себя, а также на 1, 2 и 3, причем 6 = 1+2+3.
Число 28 имеет пять делителей, кроме самого себя: 1, 2, 4, 7 и 14, причем, аналогично, 28 = 1 + 2 + +4 + 7 + 14.
Легко заметить, что далеко не всякое натуральное число равно сумме всех своих делителей, отличающихся от этого числа. Числа, которые обладают этим свойством, математиками древней Греции были названы совершенными.
Каждое такое число обозначим символом Vn, где n -номер, совершенного числа.
Тогда первое, самое меньшее совершенное число V1 =6.
Может быть, именно поэтому шестое место считалось самым почетным на пирах у древних римлян.
Второе по старшинству совершенное число V2 =28. В некоторых ученых обществах и академиях полагалось иметь 28 членов. Почти до наших дней дожила эта традиция, идущая из далеких эпох. В Риме в 1917 г. при выполнении подземных работ обнаружилось помещение одной из древнейших академий: зал и вокруг него 28 кабинетов - как раз по числу членов академии.
Лев Николаевич Толстой не раз бывало шутливо «хвастался» тем, что дата его рождения (28 августа по календарю того времени) является совершенным числом. Год рождения Л. Н. Толстого (1828) - тоже интересное число: последние две цифры (28) образуют совершенное число; если обменять местами первые цифры, то получится
V 4 = 8128 - четвертое совершенное число.
Третье совершенное число
V3 = 496,
причем 496 = 1+2 + 4+ 8 + +16 + 31 + 62 + 124 + 248.
Первые четыре совершенных числа:
6,28, 496, 8128
были обнаружены очень давно, 2000 лет назад.
Пятое совершенное число
V5 = 3 3550336
было выявлено лишь 500 лет назад (в 1400 г.).
В настоящее время зарегистрировано пока 20 совершенных чисел, причем последние восемь были обнаружены с помощью электронных вычислительных машин. Например, восемнадцатое совершенное число состоит из 1937 цифр. V18 =23216 (23217 -1). (О свойствах совершенных чисел см. на стр. 382.)
325
фель - XVI в.). Сначала появился способ сложения и вычитания, а затем и другие (подстановки, сравнения). У Ньютона в его лекциях, изданных в 1707 г., применяются уже все эти способы.
Есть ли еще такие числа?
Десятизначное число 4938271605 с неповторяющимися цифрами при делении на 9 дает симметричное частное. Действительно,
4 938271605:9=548696845. Полученный результат одинаково читается как слева направо, так и справа налево.
Пока удалось обнаружить еще только два аналогичных десятизначных числа с неповторяющимися цифрами, каждое из которых при делении на 9 дает симметричное частное. Попробуйте открыть эти или аналогичные им числа самостоятельно. Ответ на стр. 373.
Уравнения второй степени умели решать вавилоняне во втором тысячелетии до н. э., но их знания в этом вопросе не оказали влияния на развитие европейской науки, так же как и достижения других восточных народов, долго остававшиеся в Европе неизвестными. Древнегреческие математики периода до начала нашего летосчисления решали квадратные уравнения геометрическими построениями. Таково, например, приводимое в наших учебниках деление отрезка в крайнем и среднем отношении, данное Евклидом (III в. до н. э.). В более позднее время Герон и Диофант указали приемы, по существу совпадающие с нашими способами. В рукописях индийских и китайских математиков, написанных в первых веках новой эры, встречаются отрицательные корни квадратных уравнений. Однако индийский математик Бхаскара (XII в.) отмечал: «Люди отрицательных корней не одобряют».
Большие заслуги в развитии учения о квадратных уравнениях имеет уже упомянутый среднеазиатский математик ал-Хорезми. Он дает вывод правила решения квадратного уравнения, который излагается доныне во многих учебниках.
Ал-Хорезми решает уравнение x² +10 x =39 (задача 7 его сборника) следующим образом. Искомое х есть сторона квадрата, площадь которого х² . Построим на каждой стороне квадрата прямоугольники с шириной, равной четверти коэффициента второго члена уравнения,
т. е.10/4=5/2. Площадь четырех прямоугольников
равна 4· ( 5/2) x =10 x .
Площадь образовавшейся крестообразной фигуры, обведенной на чертеже сплошными линиями, равна x² +10 x, т. е. левой части данного уравнения (39). Дополним эту фигуру четырьмя квадратиками, площадь каждого из которых равна (5/2)². Получаем квадрат, стороны которого равны х +2 · ( 5/2) = х +5. Площадь образовавшегося большого квадрата (х+5)² Ее мы получили, добавив в крестовидной фигуре с площадью x² +10 x =39 площади четырех квадратов
со стороной 5/2, т. е. 4·(5/2)² =25.
Ал-Хорезми получает: ( x +5)² =39+25=64, x +5=8, x =8-5, x =3.
При буквенных обозначениях для коэффициентов уравнения x² +px=q и рассмотрении двух значений корня имеем:
Так рассуждал ал-Хорезми при решении квадратного уравнения.
326
В Европе формулами для решения квадратных уравнений различных видов владел Леонардо Пизанский в начале XIII в.; владели ими, конечно, и позднейшие математики. Вывод формулы в общем случае имеется у Ф. Виета (XVI в.), но и он признавал только положительные корни.
Итальянские математики XVI в. (Дж. Кардано, Н. Тарталья, Л. Феррари, Р. Бомбелли) присоединили к положительным корням не только отрицательные, но и мнимые. С этого времени способ решения квадратных уравнений достиг нынешнего вида.
К уравнениям третьей степени пришли греческие математики (Гиппократ, Архимед и др.) при решении геометрических задач: удвоение куба - нахождение ребра куба, имеющего двойной объем данного куба; трисекция угла - деление произвольного угла на три равные части и др. Геометрическое решение этих задач столкнулось с невозможностью построить циркулем и линейкой отрезок, выражаемый кубическим корнем. Эти задачи решались геометрически при помощи кривых - гиперболы, параболы и др. Все возможные случаи решения кубического уравнения геометрическими методами рассмотрел среднеазиатский математик и знаменитый поэт Омар Хайям на рубеже XI и XII вв. Алгебраическое решение кубического уравнения, т. е. открытие формулы, которая позволяет выразить корни всякого уравнения третьей степени через его коэффициенты, нашли в XVI в. итальянские математики С. Ферро, Н. Тарталья и Дж. Кардано. Эта формула носит имя Кардано, хотя он не являлся основным действующим лицом в данном открытии и сам признавал это. Существенно важным при решении кубического уравнения в общем случае явилось выражение корней в тригонометрической форме.
Алгебраическое решение уравнений четвертой степени в общем случае нашел Л. Феррари, ученик Кардано. Свой особый способ для этого дал Л. Эйлер в 1732 г.
Очень многие крупнейшие математики предпринимали попытки решить алгебраические уравнения пятой степени в общем случае, т. е. пытались найти формулу, при помощи которой можно было бы вычислить корни любого уравнения пятой степени по его коэффициентам. Эти усилия не дали результата. Многие математики (Г. Лейбниц, Л. Эйлер, К. Гаусс) высказывали мысль, что для уравнений пятой и более высоких степеней в общем случае не существует алгебраической формулы для выражения корней через коэффициенты. Доказал это положение в 1824 г. норвежский математик Н. Абель.
Формула Кардано для решения уравнения x³ + рх + q =0.
Однако многие частные виды таких уравнений могут быть решены алгебраически.
Французский математик Э. Галуа указал в 1830-1832 гг. метод, при помощи которого по виду уравнения можно установить, решается оно алгебраически или нет.
Голландский математик А. Жирар (1629) высказал предположение, что уравнение n -й степени имеет n корней, если считать корнями отрицательные и мнимые выражения (сам Жирар не считал их корнями уравнения). Смелее эту мысль выразил в середине XVII в. Р. Декарт, со всей же определенностью - И. Ньютон в конце XVII в.
Л. Эйлер в 1742 г. заявил, что всякое алгебраическое выражение может быть разложено на множители с действительными коэффициентами первой или второй степени. Эта мысль в иных словах означает, что всякое алгебраическое уравнение имеет корень, который может быть числом действительным или мнимым, одним словом - комплексным.
327
Так в разное время обозначали неизвестное в уравнениях.
Строго это доказал двадцатидвухлетний К. Гаусс в 1799 г.
Для вычисления приближенных значений корней уравнений высших степеней существует много приемов, которые часто применяются на практике и к уравнениям третьей и четвертой степеней, так как абсолютная точность корня на практике не всегда нужна, а применение формул сложно. Самаркандский математик ал-Каши (XV в.) дал удобную приближенную формулу для нахождения корней уравнений третьей степени, а И. Ньютон и другие - для уравнений любой степени. Очень важный метод для этого дал Н. И. Лобачевский.
Сомножители» производящие кучу пулей
Попытайтесь получить тысячу миллионов (1 000 000 000), перемножая два целых числа, в каждом из которых не было бы ни одного нуля.
Это не головоломка, для решения которой потребовалось бы выполнить много испытаний. Опираясь лишь на самые начальные сведения из алгебры, можно найти метод подбора требуемых сомножителей.
А если метод будет найден, то вы с удовольствием и без больших усилий убедитесь в том, что и квинтиллион (1 000 000 000 000 000 000) легко разлагается на два сомножителя, в каждом из которых нет ни одного нуля. Ответ на стр. 373.
Когда приходится иметь дело с большим числом (а тем более с бесконечным множеством) предметов, для различения их друг от друга удобно называть их не случайными именами (Ваня, Маша, Лондон, Амазонка...), а так, чтобы по каждому «имени» легко было отыскать соответствующий ему предмет и, наоборот, для каждого предмета легко узнать его имя в данной системе наименований. Адрес: «Такой-то переулок, дом 7, квартира 6» много удобнее, чем то, как писали еще в начале нашего века: «Дом Жукова, квартира Еремеева». На билете написано: «Ряд 5, место 4», или, короче, «5,4»; эта надпись заменяет «имя» театрального кресла (рис. 1), а сами числа 5, 4 называются его координатами (заметьте, что «4, 5» - это совсем другое кресло: важен порядок). Почти так же просто дать «имя» каждой точке, например, того листа книги, который вы сейчас читаете: расстояние этой точки от левого края листа обозначим через х, расстояние от нижнего края - через у, и будем считать пару чисел (х, у) названием этой точки. Измеряя расстояния сантиметрами, верхнему правому углу страницы дадим «имя» (20, 26), нижнему правому - (20, 0), центру листа - (10, 13). Все точки листа (а их бесконечно много!) получат свои «имена». Подобным же образом каждая точка вашей комнаты получит свое «имя» (х, у, z), здесь х - расстояние (в метрах) от северной стены, у - расстояние от западной стены, z - расстояние точки от пола; вы легко найдете, например, точку (3, 2, 1). Координата х для точки, находящейся за северной стеной, считается отрицательной, так же как у - для точки за западной стеной и z - для точки нижних этажей. Те плоскости,
328
от которых отсчитываются расстояния х, y, z, называются координатными плоскостями (на каждой из них одна координата равна нулю), а линии их пересечения - осями координат; например, прямая, вдоль которой у и z равны нулю, называется осью х.
Читатель, вероятно, хорошо знает, что такое долгота и широта места на поверхности Земли. Это географические координаты. Так, долгота Москвы +37°,5 (значит, к востоку от гринвичского начального меридиана), а широта +55°,8 (значит, к северу от экватора), поэтому координатное обозначение Москвы записывается так: 37°,5; 55°,8.
Координаты в геометрии. Числа играют важную роль в геометрии. При их помощи мы оцениваем размеры предметов. Длины, площади, объемы после выбора единицы измерения выражаются числами. Можно ли при помощи чисел описать форму предметов, форму самых причудливых фигур? Мы знаем, что углы треугольника определяют его форму («два треугольника с равными углами подобны», т. е. имеют одинаковую форму), значит, в некоторых случаях числа могут охарактеризовать форму - в данном случае два числа - два угла. Но можно ли форму любой фигуры описать при помощи чисел? Положительный ответ дает координатный метод, введенный в математику в середине XVII в. французскими учеными П. Ферма и Р. Декартом1. Это способ изучения фигур аналитически, т. е. при помощи вычислений. Ветвь геометрии, изучающая фигуры этим способом, называется аналитической геометрией.
Чтобы изучать фигуры, нужно прежде всего уметь точно описывать их. Описание должно быть полным: прочтя такое описание, мы должны суметь по нему восстановить фигуру, т. е. построить фигуру точно такую, как та, с которой было составлено описание. Говорят, что таким описанием фигура задана (однозначно), а само описание называют заданием фигуры. Каждую геометрическую фигуру будем представлять себе состоящей из точек: фигура - это множество точек (конечное или бесконечное).
Если фигура Ф состоит из конечного числа точек (или конечным числом точек однозначно определяется: например, многоугольник - своими вершинами), то для ее полного описания достаточно задать каждую из этих точек. В случае бесконечного множества точек дело обстоит сложнее (см. стр. 331), но все же сперва нужно уметь задавать положение отдельных точек, Рассмотрим точки и фигуры на плоскости.
Пять зашифрованных действий
Расшифруйте эти пять равенств, заменяя звездочки цифрами так, чтобы в каждом равенстве появились все 10 цифр от 0 до 9.
Числа, образующие первые четыре действия, не должны совпадать.
Ответ на стр 373.
1 Идея координат существовала задолго до Ферма и Декарта, ее можно проследить еще в древнем мире: в незапамятные времена художники пользовались координатной сеткой для перенесения изображений на другую плоскость; вероятно, еще древнее - вышивание по канве, которая представляет собой, так сказать, материализованную координатную сетку. Сферическими координатами (долготой и широтой) пользовалась астрономы древнего Вавилона и Египта.
329
Положение точки на плоскости можно задать при помощи двух чисел х и у, если предварительно: 1) выбрать на этой плоскости две какие-нибудь взаимно перпендикулярные прямые (обычно одну горизонтальную, другую вертикальную: например, на листе бумаги - нижний и левый его края), 2) снабдить эти прямые направлениями (например, направо и вверх) и 3) условиться о единице для измерения длин (например, сантиметр). Точку О пересечения прямых называют началом, а сами направленные прямые - осями координат: первую из них - осью Ох или осью абсцисс, вторую - осью Оу или осью ординат. Теперь для задания положения точки нужно лишь указать: 1) на каком расстоянии от оси Оу она находится: это расстояние, взятое со знаком «+» или «-», обозначается буквой х и называется абсциссой точки; 2) на каком расстоянии она лежит от оси Ох; это расстояние, со знаком «+» или «-», обозначается у и называется ее ординатой. Если точка лежит по ту сторону от оси Оу, куда направлена ось Ох, то для абсциссы берут знак «+», в противном случае - знак «-». Подобным же образом выбирается знак «+» или «-» для ординаты. У точек самой оси Ох ординаты равны нулю (у=0), у точек оси Оу абсциссы равны нулю ( x =0). Если у точки А абсцисса равна х, а ордината равна у, то пишут: А (х; у) (рис. 2). Числа х, у называют декартовыми координатами точки (х; у).
В обозначении (х; у) на первом месте всегда стоит абсцисса, на втором - ордината. На рис. 3 указаны знаки координат для точек различных координатных углов (четвертей, или квадрантов): на первом месте - знак абсциссы, на втором - знак ординаты. Обе координаты начала О равны нулю, что записывают так: 0(0; 0).
Задача 1. Проверьте правильность обозначения точек на рис. 4.
Нужно привыкнуть безошибочно решать при заданном расположении и направлении осей и заданной единице длины две первоначальные задачи: 1) найти координаты каждой указанной на рисунке точки, 2) по заданным координатам х, у построить точку
(х;у).
Вот пример более сложной задачи: Задача 2. Построить пятиугольник ABCDE, если А (-3; 1), В (2; -2), С (0; 3 1/2), D (-2;-2), E (3;1).
Задача 3. Какую фигуру образуют все точки, у которых: 1) абсцисса равна нулю ( х =0); 2) ордината больше двух ( y >2); 3) абсцисса равна ординате (х=у); 4) х=-у; 5) | х |=| y | (где | х | - обозначение для абсолютной величины числа х: если х отрицательно, то |х| =- х, в противном случае | х |= x); 6) x =0 и y >2.
При решении геометрических задач координатным методом постоянно приходится опираться на несколько совсем простых стандартных задач: определение расстояния между точками, отыскание середины отрезка и др. При этом нужно иметь в виду, что выражение «дана точка» означает, что дано ее координатное обозначение ( х; у), т. е. заданы два числа х, у. «Найти точку» - означает найти ее координатное обозначение ( х; у).
1) Расстояние между двумя точками.
Задача. Даны две точки А1 (х1 ; y1) и А2 ( х2 ; у2). Найти расстояние между ними (рис. 5).
Проведя вспомогательные линии, читатель без труда убедится, что искомое расстояние
330
d служит гипотенузой треугольника с катетами | х2 - x1 | и | y2 - y1 |, поэтому
d =+ √‾(( х2 - x1)² + (у2 - y1)²) (1)
(при возведении в квадрат знак абсолютной величины опущен, что, конечно, не меняет результата).
Важно заметить, что формула (1) верна при любом расположении точек A1 и А2. Проверьте, что, например, для А1 (-1; -2), A2 (3; -5) катеты будут действительно равны |3-(-1)| и |(-5)-(-2)| и формула (1) дает:
d =+ √‾( 4² +(-3)²)=5.
Для аналитической геометрии общность формул имеет очень большое значение. Благодаря этой общности при решении задач аналитически не нужно задумываться о том или ином расположении данных точек; можно решать задачу, даже не глядя на чертеж. Если чертеж и делается, то обычно лишь приблизительный, который служит только схемой, местом, куда записываются данные (координатные обозначения точек и пр.), а затем заносятся и найденные уже промежуточные и, наконец, окончательные результаты.
2) Середина отрезка.
Задача. Даны концы отрезка А1 (х1 ;у1) , А2 ( x2 ; у2) Найти его середину М. Обозначим координаты искомой середины М через x , у: М (х; у). Теперь, из рис. 6, видно, что
ордината у служит средней линией трапеции, поэтому
y =( y1 +y2) / 2. . (2)
точно так же
x =( x1 + x2)/2. (2)
Если знаки у1 и y2 противоположны, то это доказательство неубедительно, однако формулы (2) остаются справедливыми во всех случаях. Проверьте это.
Задача 4, Дан треугольник А B С: 4(12; 6), В (-2; 4), С (6; -2). Найти длины его сторон и медиан.
Задача 5. На оси Ох найти точку М, которая находилась бы от точки А (3; -1) на расстоянии, равном 5.
Решение. Обозначим координаты искомой точки М через (х; у). Она лежит на оси х, следовательно, y =0. Остается определить х. Записав аналитически (см. формулу (1) условие задачи: АМ= 5, получим уравнение для определения х
Задача 6. Найти точку М (х; у), находящуюся на равных расстояниях от осей координат и удаленную на 5 единиц от точки А (-1; 6). Для определения х, у нужно лишь решить систему | x |=| y |, (x+l)² +(y-6)² =5². Всего четыре ответа.
Для задания фигуры Ф в этом случае стараются подыскать такое условие, которому: 1) удовлетворяют координаты х, у всех точек из Ф; 2) не удовлетворяет ни одна чужая точка (т.е. не принадлежащая Ф). То, что здесь сказано, станет понятнее на следующих примерах:
1. Подыщем условие для фигуры, состоящей из всех точек оси Ох. Координаты всех ее точек удовлетворяют уравнению y =0, и, конечно, ни одна чужая точка ему не удовлетворяет, так как она лежит либо выше оси Ох (тогда у >0), либо ниже (тогда y <0). Уравнение y =0 и служит искомым условием.
2. Все точки биссектрисы координатного угла хОу удовлетворяют уравнению х=у, и ни одна чужая точка. (Биссектриса считается продолженной бесконечно в обе стороны.)
3. Все точки внутренней части координатного угла хОу удовлетворяют системе неравенств x >0, y >0. Эта система служит усло-
331
вием, задающим фигуру Ф - внутренность угла хОу.
4. Все точки М (х; у) окружности радиуса 5 с центром в начале координат удовлетворяют уравнению x² + y² =25, так как для любой ее точки расстояние от начала равно 5: ОМ = 5, или, на основании теоремы Пифагора, √‾(x ² + y²) = 5, что равносильно написанному выше уравнению. Для всех лежащих внутри окружности точек OM <5, т. е. х² + y² <25; для всех лежащих вне окружности OM >5, или x² + y² >25. Итак, для всех точек нашей окружности, и только для них, справедливо уравнение
x² + y² -25=0.
Такое уравнение, которому удовлетворяют все точки некоторой линии и не удовлетворяет ни одна посторонняя точка, называется уравнением этой линии; х, у в уравнении линии называют текущими координатами.
Отметьте на чертеже точки с целочисленными координатами, для которых левая часть x² + y² -25>0, знаком «+»; те, для которых она отрицательна, - знаком «-»; точки, где она равна нулю, заключите в совсем маленький кружочек. Можно ограничиться, например, лишь теми целочисленными точками, для которых | x |+| y |³ 8. Проделав это, вы отчетливо поймете, что на координатной плоскости соответствует уравнению, что - неравенству (рис. 7).
5. Уравнение x + y =5 представляет собой уравнение прямой. Попробуйте доказать это сами! (Ниже будет показано, что всякое уравнение первой степени между х и у дает уравнение некоторой прямой.) Построить эту прямую (как и всякую) очень просто: достаточно подобрать две точки, удовлетворяющие этому уравнению,
например (0; 5) и (1; 4), и затем, построив их, соединить линейкой. Снова заметим: прямая делит плоскость на две части, для одной из них (верхней) x + y >5, для другой x + y <5.
6. Попробуйте выяснить геометрический смысл неравенства |x| + |y|<5. Для этого сначала следует построить линию | x |+| y |=5. (Мы говорим: «линия | x |+ |y| =5»; это значит - линия, определенная уравнением |x|+|y|=5.) Она состоит из четырех частей. Построение следует вести отдельно в каждой из координатных четвертей: 1) при x³ 0, y³ 0, 2) при x <0, y³ 0, 3) при x <0, y <0 и 4) при x³ 0, y <0.
7. Уравнение х³ +ху² - 4x=0 определяет фигуру, составленную из окружности и вертикальной прямой, проходящей через ее центр. Действительно, данное уравнение можно переписать так: x ( x² + y² -4)=0, но произведение может быть равно нулю тогда, и только тогда, когда хоть один из множителей равен нулю, т. е. х =0, или х² +у² -4=0; первое есть уравнение оси Оу, второе - окружности (рис. 8).
8. у=х² служит уравнением параболы. Построим ее по уравнению. Для этого напишем сначала таблицу, помещая в первой ее графе произвольные значения х, например x =-3, -2 1/2, -1, 0,1, 2, 3, 4, ..., а во второй - соответствующие значения y =9, 6 1/4 ,1, 0, 1, 4, 9, 16,.... Если бы мы были в состоянии составить таблицу для всего бесконечного множества действительных чисел х и соответствующих y, а затем построили бы все такие точки ( x ; y), то эти точки сами заполнили бы собой всю искомую кривую (рис. 9). Фактически же мы вычислили координаты лишь точек: (-3; 9), (-2 1/2 ; 6 1/4), (-1; 1), (0; 0); (1; 1), (2; 4), (3; 9), (4; 16). Соединив их от руки плавной кривой (этим мы заполняем пробелы, соответствующие проме-
332
жуточным значениям x, не включенным в таблицу), получим кусок параболы между точками (-3; 9) и (4; 16). Конечно, это приблизительное построение; оно будет тем точнее, чем больше построим промежуточных точек.
Заметим, что неравенство y >x² определяет часть плоскости над параболой, а неравенство y < x² - часть плоскости под ней.
9. Уравнение ху= 12 (рис. 10) определяет на плоскости хорошо известную вам кривую - гиперболу (вспомните геометрическое изображение закона Бойля-Мариотта). Для ее построения решим уравнение относительно у:
у=12/ x
и далее строим по точкам, как это делалось в предыдущей задаче.
Прямая - это простейшая из линий; уравнение первой степени - простейшее из уравнений. И вот оказывается, что: 1) всякая прямая задается некоторым уравнением первой степени и 2) все точки, удовлетворяющие заданному уравнению первой степени относительно х и у, заполняют некоторую прямую, т. е. такое уравнение и служит уравнением прямой.
Докажем, что:
1. Уравнение всякой прямой есть уравнение первой степени.
Прежде всего это ясно для прямой, параллельной оси Оу (в частности, и для самой оси Оу), так как у всех точек такой прямой абсцисса одна и та же, т. е. равна некоторому постоянному а; x =а - это и есть уравнение рассматриваемой прямой, но оно первой степени.
Рассмотрим теперь любую прямую и, непараллельную Оу. Она пересекает Оу в некоторой точке В (0; b) (абсцисса точки В равна нулю, а ордината имеет некоторое значение b). Передвинем прямую n параллельно себе так, чтобы она прошла через начало О (0; 0). Составим прежде всего уравнение этой вспомогательной прямой. На ней найдется точка Е с абсциссой, равной 1 (это точка ее пересечения с прямой х =1); пусть ордината этой точки равна числу k: E (1; k). Тогда для любой точки нашей прямой y:x = k:1. Действительно, треугольники ОМ1 М и ОЕ1 Е подобны, поэтому их катеты | y |, | x |, | k |, 1 пропорциональны | y |:|х|= | k |:1 (рис. 11). Остается проверить лишь знаки: чертеж показывает, что если k положительно, то для любой точки прямой ОЕ непременно х и у будут или оба положительны, или оба отрицательны. Значит, равны и знаки отношений у.х, k :1. Если k отрицательно, то знаки
333
х и у противоположны (рис. 12) и равенство y : x=k :1, или y=kx, остается в силе. При k =0 точка Е лежит на оси х, прямая ОЕ совпадает с осью Ох, а уравнение у =kx превращается в y =0. Итак, при любом k уравнением вспомогательной прямой ОЕ служит равенство y=kx. Вернемся теперь к первоначальной прямой и; ее можно получить из вспомогательной прямой ОЕ сдвигом в направлении оси у на отрезок b . Это значит, что каждая ее точка перемещается в направлении оси Оу на b (если b >0- вверх, если b <0 - вниз).
Ордината каждой точки при этом изменится на одно и то же число b , а абсцисса останется прежней; вместо уравнения y=kx вспомогательной прямой мы теперь получим:
у = kx+b.
Это и будет уравнением прямой п. (Напомним, что ни одна чужая точка этому уравнению не удовлетворяет: для точек, лежащих выше нашей прямой, y>kx+b, для точек, лежащих ниже, y<kx+b; k называется угловым коэффициентом прямой, b - начальной ординатой.) Из треугольника ОЕЕ1 легко выяснить геометрический смысл углового коэффициента прямой: это тангенс угла, который наша прямая образует с положительным направлением оси Ох. Если угол тупой, то k отрицательно. 2. Всякое уравнение первой степени
Ах + By + С = О (3)
есть уравнение некоторой прямой. Действительно, А и В сразу оба не могут быть равны нулю (так как тогда наше уравнение не было бы первой степени). Пусть, например, B ¹ 0, тогда уравнение можно разрешить относительно у; оно примет вид: у =-( A/B)x-C/B. Если теперь построить прямую с угловым коэффициентом k, равным - A/B, и начальной ординатой b, равной - C/B, то, как мы уже видели, ее уравнение будет: у = kx + b, или y =-( A/B) x+ (- C/B), т. е. равносильно заданному. (Случай В=0; A ¹ 0 приведет к уравнению х =- C/A, т. е. х постоянно. Это уравнение прямой, параллельной оси Оу; при C =0 - сама ось Оу.)
Как мы видели, прямая однозначно определяется ее уравнением. Поэтому уравнение прямой может служить как бы ее «именем»; постоянно говорят: «прямая Ах+Ву+С=0»; это значит, что прямая задана уравнением Ах+Ву+С=0.
1) Построение прямой по ее уравнению. Чтобы построить прямую по ее уравнению, проще всего найти какие-нибудь две точки, удовлетворяющие этому уравнению; построив их, проводим через них прямую.
Пример. Построить прямую 2х- З y +8=0. Этому уравнению удовлетворяют точки (-4; 0), (-1; 2), (5; 6),.... Строим какие-нибудь две из них (лучше не слишком близкие, иначе проведение через них прямой по линейке не будет достаточно точным), например (-4; 0) и (5; 6), и соединяем линейкой.
2) Даны две различные точки A1 (х1 ; у1) и А2 ( x2 ; y2). Найти прямую А1 A2. (Это значит найти ее уравнение.)
334
Проверим, что искомое уравнение можно записать так:
(х-х1)· ( y2 - у1)-(у- y1) ·( x2 - х1) = 0. (4)
Прежде всего это уравнение первой степени относительно текущих координат х, у, - значит, оно есть уравнение прямой. Подставив вместо текущих координат x и y сначала x1 и y1, а затем x2 и y2, убеждаемся каждый раз, что уравнение обращается в тождество, - значит, эта прямая проходит и через точку ( x1 ; y1), и через точку ( x2 ; y2).
Обычно уравнение (4) записывают в более удобной для запоминания форме:
( x- х1)/( x2 -x1) = ( y-y1)/( y2 -y1). ( 4')
Однако последняя перестает служить, если х1 =х2 или у1 =у2.
3) Даны две прямые: Ах+Ву+С=0 и А'х+ B 'y+C'=0. Найти точку их пересечения. Точка пересечения лежит на той и на другой прямой, следовательно, ее координаты должны удовлетворять обоим уравнениям. Итак, для нахождения их надо решить совместно эти уравнения (система двух уравнений с двумя неизвестными).
4) Как следует из сказанного ранее, угловой коэффициент k характеризует направление прямой, поэтому равенство угловых коэффициентов двух прямых означает их параллельность. Так как k=-A/B, то условие параллельности ( k = k ') прямых Ах+Ву+С= 0 и A'x+B'y+C'= 0 может быть записано и так:
А : В=А' : В'. (5)
5) Условие перпендикулярности. Если прямые перпендикулярны, то углы a и a ', образуемые ими с осью Ох, разнятся на 90°: a ' = a +90°, поэтому их угловые коэффициенты k и k' удовлетворяют равенству kk' =- 1. Это легче всего усмотреть из рис. 13: на нем треугольник ОЕЕ' прямоугольный, k и - k' служат проекциями катетов на гипотенузу, поэтому их произведение равно квадрату высоты: k · (-k') =OE1² =1. Иначе условие перпендикулярности
пишут в виде: k' =-1/ k или, в силу равенств
k=-A/B, k' А=- A/B, в виде:
АА'+ВВ'= 0. (6)
Задача 7. Через точку (2;-3) провести прямую, перпендикулярную прямой 4х- 3y +2=0.
Решение. Для изменения направления на перпендикулярное достаточно (выполняя условие (6) обменять местами коэффициенты А, В и у одного из них изменить знак: А =4, В= - 3; теперь возьмем A '=+3, B '=4. Уравнение искомой прямой уже можно написать: Зх+4 y + C '=0. Неизвестный пока член С' определится из требования, чтобы данная точка (2;-3) лежала на этой прямой: 3·2+4·(-3)+С'=0, или C' =6.
Ответ: 3 x +4 y +6=0.
6) Расстояние между точкой и прямой. Решим частный случай этой задачи: найти длину р перпендикуляра из начала О (0; 0) на прямую A х + By + С =0. Решение удобно вести по такой схеме:
1. Найти уравнение перпендикуляра из О (0; 0) на Ах+Ву+С =0 (см. задачу 7).
Ответ: Вх-Ау= 0.
2. Проекция О' начала О на данную прямую получается совместным решением уравнений:
Ах+Ву+С= 0 и Вх-Ау= 0.
Ответ: x=- w /( A² +В²) y=-CB /( A² +B²)
3. Остается найти искомое расстояние р как расстояние между О и О':
Общий случай: «найти расстояние d от точки Р0 ( х0 ; у0) до прямой Ах+Ву+С =0 - может быть решен тем же путем. В результате получим, что искомое расстояние
335
т. е. расстояние от точки (х0 ;у0) до прямой Ах+Ву+С= 0, равно частному от деления абсолютной величины результата подстановки в левую часть уравнения прямой координат точки (х0 ;у0) на «нормирующий» корень √‾( A² +B²).
Как известно, окружностью называется множество точек плоскости, находящихся от заданной точки Г (центра) на заданном расстоянии R (радиус). Запишем это определение аналитически относительно декартовой системы координат. Пусть С (а; b). Тогда для любой точки Р (х; у) окружности PC=R, т. е.
√‾ ( ( x- а)² + ( у- b)²)= R,
или
(х-а)² + (у- b)² = R² (8)
Это и есть (общее) уравнение окружности. Раскрыв в нем скобки
x² +y² - 2 ах- 2 by+a² +b² -R² =0, убеждаемся, что это есть частный случай общего уравнения второй степени относительно х и у:
Ах² +Вху+Су² + Dx+Ey+F =0. (9) В нашем случае A=C=1, B =0. Оказывается, что всякое уравнение второй степени относительно декартовых координат х, у, в котором коэффициенты при х² и y² равны (и по абсолютной величине и по знаку: А=С), а коэффициент при ху равен нулю ( B =0), либо является уравнением некоторой окружности (быть может, нулевого радиуса), либо ни одна (действительная) точка плоскости ему не удовлетворяет.
Задача 8. Построить окружность 2х² +2 y² +З y =0. Пишем уравнение так:
x² +y² +(3/2)y +9/16=9/16,
или x² +( y +3/4)² =(3/4)². Сравнивая с общим
Координатная система в поэзии Н. А. Некрасова
... идите по лесу
Против столба тринадцатого
Прямехонько версту:
Придете на поляночку,
Стоят на той поляночке
Две старые сосны ... (Кому на Руси жить хорошо).
«Тринадцатого» и «версту» - координаты поляночки с двумя старыми соснами.
уравнением окружности, видим, что а= 0 , b =-3/4,
R=3/4. Теперь легко выполнить построение.
Если в общем уравнении второй степени А ¹ С или В ¹ 0, то такое уравнение уже не будет задавать окружности. Оказывается, возможны здесь только такие линии: парабола, эллипс (см. пример 2 на стр. 336, 337), гипербола или (если левая часть уравнения разлагается на множители первой степени) пара прямых. Все они называются линиями второго порядка. Впрочем, бывает и так, что ни одна точка плоскости уравнению не удовлетворяет, например: 2 x² +3 y² +1=0 (мнимый эллипс).
При решении геометрической задачи аналитическим методом прежде всего выбирают систему координат (от удачного выбора ее зависит простота вычислений). Затем находят в этой системе координаты заданных точек и уравнения заданных прямых, окружностей и т.д. Этим задача переводится на аналитический язык и превращается в задачу аналитической геометрии.
Пример 1. Доказать, что три высоты треугольника А B С всегда пересекаются в одной точке.
Примем одну из высот ОС за ось Оу, а соответствующее основание А В - за ось Ох. Координатное обозначение вершин: А (- р; 0), B(q; 0), С (0; h) (h - высота, р, q - проекции сторон СА и СВ на основание). По формуле (4) составляем уравнения боковых сторон:
hx- ру + ph =0 (СА), hx+qy+ph= 0 (CB).
(Сделайте проверку: (- р ; 0) лежит на СА, (0; h) - тоже.) Составляем уравнения боковых высот: px+hy=pq, qx-hy=-pq (см. задачу 7). Точка пересечения (0; pq/h), найденная совместным решением их уравнений, очевидно, лежит на третьей высоте, так как ее абсцисса равна нулю, и т. д.
Пример 2. Эллипс. Выяснить, какую кривую опишет точка тонкой прямолинейной палочки, скользящей своими концами по неподвижным взаимно перпендикулярным прямым Ох и Оу.
Примем эти прямые за оси координат. Расстояния точки от концов палочки обозначим
336
через а и b (постоянные числа, так как точка по палочке не двигается).
Обозначим через t (переменный) угол, образованный палочкой с отрицательным направлением оси Ох. На рис. 14 видно, что
x=acost, y=bsint.
Эти два уравнения можно рассматривать как особый вид уравнений кривой. Здесь связь между х и у задана при помощи вспомогательного переменного (параметра) t. Такие уравнения кривой называются параметрическими.
По ним построение кривой делают так: дают произвольные значения параметру t, каждый раз вычисляя соответствующие значения x и y, что определяет точку кривой. Так, точка за точкой можно построить сколько угодно точек кривой. Если вы хотите получить обычное ее уравнение, следует исключить из параметрических уравнений параметр t (не всегда это легко сделать!), т. е, составить их следствие, не содержащее t. В данном случае, деля эти уравнения: первое - на а, второе - на b , возводя в квадрат и складывая, получим:
( x/a)² +( y/b)² = sin² t + cos² t =1, или
x² /a² +y² /b² =1 (10)
Это простейшее уравнение эллипса. Эллипс - кривая, получаемая из круга равномерным растяжением или сжатием в одном направлении (см. статью «Геометрические преобразования»). Как известно, по эллипсам движутся планеты вокруг Солнца (первый закон Кеплера), искусственные спутники вокруг Земли.
Эллипсограф. Из рассмотренной только что задачи вытекает конструкция прибора для черчения эллипсов (эллиптический
циркуль, или эллипсограф). Для этого нужно лишь к подвижной палочке прикрепить карандаш, который можно было бы закреплять винтом в различных положениях на палочке. Этот карандаш при описанном выше движении палочки вычертит эллипс, полуоси которого а, b зависят от того, в какой точке палочки закреплен карандаш. Из уравнения (10) следует, что середина палочки описывает окружность, ведь для середины а= b ! На рис. 15 показан эллипсограф несколько иной конструкции.
Сталкиваясь впервые с задачами на построение, которые не могут быть решены циркулем и линейкой, всякий испытывает сначала неудовлетворенность, - как это нельзя решить? Между тем в этом нет ничего странного, просто циркуль и линейка - недостаточно сильные (может быть, лучше сказать - недостаточно тонкие) инструменты для решения некоторых задач. Таковы, например, задачи о делении произвольного угла на три равные части (трисекция угла) и об удвоении куба («Построить ребро куба двойного объема по сравнению с данным кубом»). Некоторые из таких задач становятся разрешимыми, если к линейке и циркулю присоединить, например, прибор, вычерчивающий параболу, или эллипсограф.
Чтобы разобраться, какие же задачи разрешимы с помощью циркуля и линейки,
будем рассуждать так. Линейка дает возможность строить прямую, проходящую через две уже построенные точки, находить точки пересечения прямых. Присоединяя к линейке циркуль, мы можем строить окружности любых данных радиусов с заданным центром, находить точки пересечения двух окружностей и окружности с прямой. Подойдем к вопросу аналитически. Прежде всего заметим, что одна линейка дает возможность решать лишь за-
337
дачи первой степени: например, пересечение двух прямых соответствует в декартовых координатах решению системы двух уравнений первой степени с двумя неизвестными. Присоединив циркуль, мы, оказывается, можем уже решать все задачи второй степени, т. е. такие, которые аналитически сводятся к решению ряда квадратных уравнений с одним неизвестным. Ведь пересечение прямой с окружностью означает совместное решение уравнения окружности и уравнения прямой; после исключения одной координаты получается квадратное уравнение с одной неизвестной координатой. Пересечение двух окружностей можно заменить пересечением одной из них с хордой, проходящей через обе точки пересечения. Аналитически это вполне ясно. Напишем уравнения этих окружностей:
х² + у² + Dx +Еу+ F =0, х² +у² + D'x +Е'у +F' =0.
Вычтя одно из другого, получим уравнение первой степени (это и есть уравнение упомянутой хорды). Значит, опять получается пересечение прямой с одной из окружностей, что (как уже было сказано) сводится к квадратному уравнению с одним неизвестным. Таким образом, циркуль и линейка способны решать лишь задачи, которые сводятся к последовательному решению ряда квадратных уравнений с одним неизвестным. Поэтому всякое уравнение, которое нельзя свести к решению ряда квадратных уравнений (например, х³ =2), не может быть решено графически циркулем и линейкой. Как раз задача об удвоении куба и есть задача о решении уравнения x³ =2: приняв за 1 ребро данного куба, для ребра х искомого получаем именно это уравнение. Задача о трисекции угла (кроме некоторых частных случаев, например угол в 90°) тоже оказывается задачей третьей степени, отсюда - невозможность решения ее при помощи циркуля и линейки.
Если же воспользоваться прибором для черчения парабол, то, вычертив две параболы х² =у и 2х=у², в пересечении получим точку, абсцисса которой как раз удовлетворяет уравнению х³ =2.
При решении многих задач удобнее пользоваться так называемыми полярными координатами: на плоскости выбирают неподвижную точку О (полюс) и выходящий из нее луч ОР
(полярная ось). Положение точки М в этом случае определяется двумя числами: ее расстоянием r от полюса и углом j = Ð РОМ (рис. 16). Числа r (полярный радиус) и j (полярный угол) называются полярными координатами точки М. Часто оказывается полезным рассматривать на плоскости полярную систему координат вместе с декартовой. Рассмотрим такое расположение, когда полюсом служит начало декартовой системы, а полярной осью - ось абсцисс;
Эти формулы позволяют вычислить декартовы координаты, когда известны полярные.
Пример. Выяснить форму кривой
( x² + y²)² =а² ( х² -у²)
(она называется лемнискатой). Исследовать ее форму непосредственно по написанному уравнению не так легко. Перейдем к полярным координатам. Заменив х и у по формулам (11), получим: r 4 = a² r² (cos² j -sin² j).
тогда рисунок подсказывает связь между полярными и декартовыми координатами точки:
Или, сократив на r² (при этом могла бы потеряться лишь одна точка кривой r =0), получим:
r² = a² cos 2 j, или r = + a √‾(cos2 j). По этому
простому уравнению легко построить нашу кривую. Кривая строится по точкам (рис. 17). Даем j различные значения, например j =0,
+15°, +30°, +45°, +135° .. Вычисляем соответствующие r = а, а4 √‾(³ /4), а √‾ ( 1/2), 0, 0.
338
При значениях j между 45 и 135°, а также между 225 и 315° косинус отрицателен и поэтому r мнимо: у кривой нет точек с такими значениями полярного угла.
Точки, у которых полярный радиус имеет постоянное значение r =С, образуют окружность радиуса С, с центром в полюсе. При постоянном значении угла j, j = j0, получается луч, выходящий из полюса и наклоненный под углом j0 к полярной оси. Полученные таким образом (т. е. при постоянном значении одной координаты) линии называются координатными (рис. 18). В декартовой системе координатные линии- прямые, параллельные осям.
Спираль Архимеда. Это кривая задается в полярных координатах уравнением r =С j , где С - постоянная (рис. 19).
При помощи этой кривой любой угол можно делить на произвольное число (например, на три - трисекция угла) равных частей. Вот как это делается (рис. 20). Пусть на листе бумаги начерчена спираль Архимеда, выходящая из полюса О полярной системы координат, полярная ось ОР служит для спирали касательной. Перенесем на этот чертеж заданный нам для разделения на n равных частей угол так, чтобы его вершина совпадала с полюсом, одна сторона - с полярной осью ОР, а другая его сторона легла в сторону возрастания полярного угла j (против часовой стрелки). Обозначим первую (считая от О) точку пересечения этой другой стороны с нашей спиралью буквой А; затем разделим отрезок ОА на n равных частей (что, как вы знаете, легко делается циркулем и линейкой) и проведем через точки А1, А2, ... деления отрезка ОА дуги окружностей с общим центром О до пересечения со спиралью; наконец, полученные точки B1, В2, ... пересечения соединим с полюсом - и данный угол POQ разделен на n равных частей! Докажите это сами.
339
Положение точки на сфере удобнее всего задавать так, как это делается в географии. На данной сфере радиуса R выберем какие-нибудь две диаметрально противоположные точки, одну из них N назовем условно северным полюсом, другую S - южным. Какой-нибудь из «меридианов» (кратчайший путь по сфере из S в N) назовем начальным меридианом; проходящую через центр О сферы и перпендикулярную оси SN плоскость назовем экваториальной, а пересечение ее со сферой - экватором, на экваторе изберем направление, скажем против часовой стрелки, если смотреть из N. Положение любой точки М на сфере определяется двумя координатами, одна из них, назовем ее долготой,-угол j между плоскостью начального меридиана и плоскостью, проходящей через М и ось SN (угол должен отсчитываться в направлении, соответствующем выбранному на экваторе). Широтой точки М будем называть угол 6 между радиусом ОМ и плоскостью экватора (6 считается положительным для точек северного полушария и отрицательным для южного). Будем писать: М < j ; q >, ставя на первое место долготу, на второе - широту.
Пример. Проверьте правильность координатного обозначения точек на рис. 21.
Все точки с одинаковой долготой j0 заполняют меридиан, уравнение которого поэтому j = j0. Все точки с одинаковой широтой q0 заполняют параллель q = q0. Уравнение, связывающее текущие координаты j и q, определяет, как и в плоской геометрии, кривую; неравенство, соответствующее этому уравнению, определяет одну или несколько областей, на которые эта кривая разделяет сферу. Так, неравенство 6< 0 определяет южную полусферу, q >0-северную; q =0 есть уравнение экватора. Если сферу отнести к декартовым координатам в пространстве, приняв центр О сферы за начало, ось SN - за ось z, ось х направив через точку <0; 0>, ось у - через<90°; 0>, то декартовы координаты х, y, z любой точки М сферы легко выразить через долготу и широту этой точки. Для этого выразим сначала координаты ее проекции М1 на плоскость Оху, где обычным образом расположим полярную систему координат. Из рис. 21 видно, что для М1 (х; у; 0) полярный радиус r=R cos q, а полярный угол j совпадает с долготой точки М. Кроме того, z=R sin q. Приняв во внимание формулы (11), получим:
По этим формулам вычисляют декартовы координаты точки М (х; у; z), если известны ее координаты j и q на сфере.
На эти же формулы можно взглянуть и с другой точки зрения. Будем считать со и 6 переменными, придавая им всевозможные значения в естественных пределах 0 £ j <360°, - 90° £ q £ +90°; тогда точка М < j ; q > будет перемещаться по сфере, занимая всевозможные положения. Это напоминает параметрические уравнения линии, в которых декартовы координаты х, y, z выражены через один переменный параметр t. Разница лишь в том, что теперь х, у, z выражены через два параметра, поэтому получается не линия (одномерное образование), а поверхность (образование двумерное). Подобные уравнения называют параметрическими уравнениями поверхности; переменные параметры чаще всего здесь обозначают буквами и ж v. Итак, уравнения сферы запишем в виде:
Если из этих уравнений исключить параметры и, v (для этого проще всего возвести (13) в квадрат и сложить; к сожалению, исключение переменных не всегда так просто), получим обычное ее уравнение x² + y² + z² =. R² .
340
На любой поверхности можно установить координатную систему, определяя положение точки на ней опять-таки двумя числами. Для этого каким-либо способом покроем всю поверхность двумя семействами линий так, чтобы через каждую ее точку (быть может, за небольшим числом исключений) проходила одна, и только одна, линия из каждого семейства. Теперь надо лишь снабдить линии каждого семейства числовыми пометками по какому-нибудь твердому правилу, позволяющему по числовой пометке находить нужную линию семейства (рис. 22).
Координатами точки М поверхности служат числа u, v, где u - числовая пометка линии первого семейства, проходящей через М, и v - пометка линий второго семейства. По-прежнему будем писать: М ( u; v), числа и, v называются криволинейными координатами точки М. Сказанное станет совсем ясным, если за примером обратиться к сфере. Ее всю можно покрыть меридианами (первое семейство); каждому из них соответствует числовая пометка, а именно значение долготы u (или j). Все параллели образуют второе семейство; каждой из них отвечает числовая пометка - широта v (или 6). Через каждую точку сферы (исключая полюсы) проходит только один меридиан и одна параллель.
В качестве еще одного примера рассмотрим боковую поверхность прямого круглого цилиндра высоты Н, радиуса a (рис. 23). За первое семейство примем систему его образующих, одну из них примем за начальную. Каждой образующей припишем отметку u , равную длине дуги на окружности основания между начальной образующей и данной (дугу будем отсчитывать, например, против часовой стрелки). За
второе семейство примем систему горизонтальных сечений поверхности; числовой пометкой v будем считать высоту, на которой проведено сечение над основанием. При надлежащем выборе осей х, у, z в пространстве будем иметь для любой точки М (х; у; z) нашей поверхности:
х= acos(u/a), у= asin(u/a), z=v, (14) 0 £ u<2 p a, 0 £ v £ H.
(Здесь аргументы у косинуса и синуса не в градусах, а в радианах.) Эти уравнения можно рассматривать как параметрические уравнения поверхности цилиндра.
Задача 9. По какой кривой надо вырезать кусок жести для изготовления колена водосточной трубы, чтобы после надлежащего изгибания получился цилиндр радиуса а, усеченный плоскостью под углом 45° к плоскости основания?
Решение. Воспользуемся параметрическими уравнениями поверхности цилиндра:
х = acos(u/a), у= asin(u/a),
z = v.
Секущую плоскость проведем через ось Ох, ее уравнение z=y. Комбинируя его с только что написанными уравнениями, получим уравнение v = a sin - линии пересечения в криво-
341
линейных координатах. После развертки поверхности на плоскость криволинейные координаты и и v превратятся в декартовы координаты.
Итак, кусок жести должен быть сверху
очерчен по синусоиде v = asin( u/a). Здесь
u и v уже декартовы координаты на плоскости (рис. 24).
Как в случае сферы и цилиндрической поверхности, так и в общем случае задание поверхности параметрическими уравнениями влечет за собой установление на поверхности криволинейной системы координат. Действительно, выражение декартовых координат х, у, z произвольной точки М (х; у; z) поверхности через два параметра u, v (это в общем случае записывают так: ж= j ( u ; v), y= y (u; v), z= w (u; v), j, y, w - функции двух аргументов) дает возможность, зная пару чисел u, v , найти соответствующие координаты х, у, z, а значит, положение точки М на поверхности; числа u, v служат ее координатами. Давая одной из них постоянное значение, например u = u0, получим выражение х, у, z через один параметр v, т. е. параметрическое уравнение кривой. Это - координатная линия одного семейства, ее уравнение u = u0. Точно так же линия v=v0 - координатная линия другого семейства.
Одним из самых важных понятий в математике и ее приложениях является понятие функции. Всюду, где есть величины, связанные так, что с изменением одних (аргументов) меняются другие (функции), мы имеем дело с функциональной зависимостью. Эта зависимость может задаваться по-разному - формулами, графиками, таблицами. Бывают случаи, когда зависимость нельзя выразить формулой. Например, температура воздуха меняется с течением времени, однако формулы, выражающей температуру воздуха в данный момент времени, нет (как легко жилось бы метеорологам, если бы такая формула была!). В некоторых случаях приходится довольствоваться графиком функции (например, самопишущий прибор термограф дает график температуры воздуха как функции времени) или только таблицей значений функции для некоторых значений аргумента.
Чаще всего, однако, для описания функций пользуются формулами. В школе изучают случаи, когда эти формулы сравнительно просты. Например, зависимость площади круга от его радиуса выражается формулой S = p r², тока от
сопротивления - формулой I = V0 /R и т. д. Возникает вопрос: встречаются ли на практике зависимости, выражаемые с помощью более сложных функций, например многочленов высоких степеней, показательной, логарифмической и тригонометрических функций? Мы расскажем здесь о некоторых случаях, когда такие функции встречаются в задачах физики и техники.
Балками в технике называют деревянные или металлические брусья, на которых лежат перекрытия зданий. Балки должны выдерживать вес перекрытий и предметов, находящихся в здании. Под этой тяжестью они изгибаются. Если балки изогнутся слишком сильно, перекрытие может рухнуть. Поэтому до постройки здания надо рассчитать, выдержат ли балки нагрузку. Этими расчетами занимается специальная наука - сопротивление материалов.
Прогиб балки зависит от очень многих причин. Под одной и той же нагрузкой деревянная балка изогнется сильнее, чем стальная, длинная - сильнее, чем короткая, тонкая - сильнее, чем толстая. Зависимость прогиба балки от материала, из которого она сделана, связана с особой величиной Е, называемой модулем Юнга.
Модуль Юнга измеряется в кГ/см². Если из вещества с модулем Юнга Е кГ/см² сделать стержень длиной 1 м и сечением 1 см² и подве-
342
сить к этому стержню гирю в 1 кГ, то он вытянется на 1/ E м. Для стали модуль Юнга равен
2 150 000 кГ/см² а для дуба - 105 000 кГ/см², т. е. в 20 раз меньше.
Чем больше модуль Юнга, тем меньше прогиб балки. Поэтому стальные балки прогибаются меньше, чем деревянные.
Исследование зависимости прогиба балки от материала, из которого она сделана, - это скорее дело физики, чем математики. Математиков больше интересует зависимость прогиба от длины балки и от размеров и формы ее сечения. А то, что форма сечения влияет на прогиб, легко видеть из простого опыта. Обычную школьную линейку легко согнуть, если положить ее плашмя, и трудно, если поставить на
Рис. 1. Линейку легко согнуть, если положить ее плашмя, и трудно, если поставить на ребро.
ребро (рис. 1). Этот опыт показывает еще, что прогиб зависит не от площади сечения (ведь площадь сечения линейки одна и та же, лежит она плашмя или поставлена на ребро). Оказывается, дело не в площади сечения, а в его моменте инерции. Момент инерции / подсчитывают так. Сечение балки мысленно разрезают на очень тонкие горизонтальные слои и площадь каждого слоя умножают на квадрат расстояния этого слоя от среднего слоя. Сумма этих произведений и дает момент инерции сечения балки. Подсчеты показывают, что момент инерции для круглого сечения радиуса R равен p R4 /4, а для квадратного сечения со стороной а равен a4 /12.
Произведение EI модуля Юнга на момент инерции сечения балки называют жесткостью балки. Чем больше жесткость, тем труднее изогнуть балку. Можно увеличить жесткость балки, не меняя площади ее сечения. Для этого надо сосредоточить основную массу балки на
большом расстоянии от среднего слоя, например придать сечению форму, изображенную на рис. 2, слева (двутавровые балки), или заменить сплошную балку трубой (рис. 2, справа). Поэтому, например, в велосипедах делают корпус не из сплошных стержней, а из труб.
Прогиб балки зависит не только от ее жесткости, но и от длины балки, распределения нагрузки, от того, заделаны ли в стену оба конца балки или только один, и т. д. Чтобы найти наибольший прогиб балки, надо знать форму, которую она принимает после изгиба.
Возьмем балку длины l, заделаем оба ее конца в стены и положим на нее равномерно распределенную нагрузку Q. Тогда прогиб у в точке, находящейся на расстоянии х от левого конца балки, выражается формулой:
y =( Q /24 EIl) ( x4 -2 lx³ + l² x²),
т. е. многочленом четвертой степени. График этого многочлена изображен на рис. За. Ясно,
что самый большой прогиб балки будет в середине, т. е. при х= l/2 . Он равен ymax = Ql³ /384 EI .
Балки, на которые опираются балконы, заделываются в стену лишь одним концом, второй же конец оставляют свободным. Такие балки называются консольными. Форма равномерно нагруженной консольной балки выражается уравнением:
y=(Q/24EIl)(x 4 - 4 lx³ + 6 l² x²)
343
(рис. 3 б). Здесь уже наибольший прогиб будет на свободном конце балки, при х= l . Он равен
ymax = Ql³ /8 EI,
т. е. в 48 раз больше, чем для такой же балки, оба конца которой заделаны,
Прогиб балки зависит и от того, как распределена нагрузка. Возьмем балку, оба конца которой свободно лежат на опорах, а нагрузку Q соберем в одну точку - середину балки (рис. 4). Тогда форма изогнутой балки будет
задаваться не одним, а двумя уравнениями. Для левой половины балки прогиб равен;
yлев. =( Q / 48 EI)[3 l² x-4 x³],
а для правой:
yправ. = (Q /48 EI)[3 l²(l - x) - 4 (l - x)³].
Наибольший прогиб равен: ymax = Ql³ /48 EI .
Замечательно, что в этом случае одна и та же функция - прогиб балки в точке, находящейся
на расстоянии х = l /2 от левого конца, - выражается не одной, а двумя различными формулами.
Перейдем теперь к случаям, когда зависимость выражается показательной функцией. При записи законов физики, связанных с показательной функцией, удобно пользоваться особым числом, которое называется числом е. Это число можно определить следующим образом. Начертим графики функций y = ax при разных значениях основания а. Чем больше это основание, тем круче поднимаются вверх графики (рис. 5). Эти графики в точке А (0; 1)
под разными углами пересекают ось Оу. Например, угол между осью Оу и кривой y=2x равен приблизительно 55°15', а для кривой y =3x этот угол равен примерно 42°20'. Поэтому найдется такое число е, лежащее между 2 и 3, что кривая у=ех пересечет ось Оу под углом 45°.
Более точные подсчеты показывают, что число е равно 2,71828... Логарифмы по основанию е называются натуральными. Они обозначаются ln x. Если мы знаем десятичный логарифм числа, то его натуральный логарифм
можно найти по формуле lnx = lgx/M, где М=0 ,43429... - так называемый модуль перехода.
Когда корабль подходит к берегу, с него бросают на пристань канат. Здесь канат обматывают несколько раз вокруг столба и таким образом удерживают им корабль. Как же
344
удается одному человеку удержать корабль? Оказывается, ему помогает сила трения. Если обмотать канат один раз вокруг столба, то из-за трения каната о столб можно уравновесить силой F0 силу F, большую, чем F0, в а
раз. Отношение F / F0 =а зависит от материала,
из которого сделаны канат и столб. Например, если канат пеньковый, а столб железный, то a =3,5. Иными словами, силой в 100 кГ можно уравновесить (используя «помощь» силы трения) силу в 350 кГ. Каждый новый оборот каната вокруг столба увеличивает отношение сил еще в а раз. Таким образом, если обернуть канат два раза, то отношение удерживаемой и
удерживающей сил будет равно а², а если три
раза, то F / F0 =a³. Вообще если число оборотов
равно х (х может и не быть целым числом),
то F/F0 = аx . Если обмотать пеньковый канат
вокруг железного столба два раза, то силой в
100 кГ можно уравновесить силу примерно в 1,2 Г, а при трехкратном обматывании - силу в 4,2 Т.
Когда радиоактивное вещество распадается, его количество уменьшается. Через некоторое время остается половина первоначального количества вещества. Этот промежуток времени t0 называется периодом полураспада вещества. Если пройдет еще t0 лет, то из оставшейся половины распадется еще половина вещества и останется только четверть первоначального количества. Вообще через t лет масса т вещества будет равна:
m = m0 ( 1/2)t/t0,
где m0 - первоначальная масса вещества. Чем больше период полураспада, тем медленнее распадается вещество. Например, у урана-238 период полураспада равен 4,5 млрд. лет. Значит, за все время существования Земли не распалось еще и половины первоначального запаса урана. А вот у радия период полураспада равен всего 1590 годам. Если бы миллион лет назад вся Земля состояла из радия, то сейчас на ней не осталось бы и одного атома радия. Существует же он лишь потому, что при распаде урана все время появляются новые атомы радия.
Если повернуть выключатель, в то же мгновение загорается электрическая лампочка. Мы настолько привыкли к этому, что не задумываемся над тем, сразу ли сила тока принимает свое максимальное значение. Соберем электрическую схему, показанную на рис. 6, и включим
ток. Тогда из-за наличия катушки ток будет нарастать медленно, так как в цепи возникнет ток самоиндукции, направленный в противоположную сторону. Расчеты показывают, что ток I зависит от времени по следующей формуле:
Здесь R - сопротивление цепи, L - самоиндукция катушки, V0 - напряжение тока. Посмотрим, что будет происходить с током с течением времени. Функцию е- Rt/L можно записать в виде (1/ e) Rt/L. Но - меньше единицы, известно, что показательная функция стремится к нулю с возрастанием показателя, если ее основание меньше единицы. Поэтому вычитаемое е- Rt/L в формуле для силы тока будет уменьшаться, приближаясь к нулю, и через некоторое время ток почти точно будет равен V0 /R. Это и есть значение, которое известно из закона Ома. Разница между силой тока и значением V0 /R
станет такой маленькой, что никакие приборы ее не покажут.
Вы, наверное, замечали, что если снять кипящий чайник с огня, то сначала он быстро остывает, а потом остывание идет гораздо медленнее. Дело в том, что скорость остывания
345
пропорциональна разности между температурой чайника и температурой окружающего воздуха. Чем меньше становится эта разность, тем медленнее остывает чайник. Если сначала
Чем больше чайник, тем значение k меньше и тем медленнее он остывает.
температура чайника равнялась Т0, а температура воздуха Т1, то через t секунд температура Т чайника выразится формулой:
Т=(Т0 -Т1)е- kt + Т1,
где k - число, зависящее от формы чайника, материала, из которого он сделан, и количества воды, которое в нем находится.
При падении тел в безвоздушном пространстве скорость их непрерывно возрастает. При падении тел в воздухе скорость падения тоже увеличивается, но не может превзойти определенной величины.
Рассмотрим задачу о падений парашютиста. Если считать, что сила сопротивления воздуха пропорциональна скорости падения парашютиста, т.е. что F=kv, то через t секунд скорость падения будет равна:
(т - масса парашютиста). Обратите внимание на сходство этой формулы с формулой для силы тока.
Через некоторый промежуток времени e-kt/m
станет очень маленьким числом и скорость падения будет почти в точности равна mg/k, т. е.
падение станет почти равномерным. Коэффициент пропорциональности k зависит от размеров парашюта.
Написанная формула пригодна не только для изучения падения парашютиста, но и для изучения падения капли дождевой воды, пушинки и т. д. Из нее видно, что чем меньше отношение mg/k, тем медленнее падает тело. Этим
и объясняется, почему пушинка падает медленнее камня: у нее маленькая масса, а площадь поверхности довольно большая, и воздух оказывает значительное сопротивление ее падению.
Парашютист опускается на землю равномерно.
Чем выше поднимаются в гору альпинисты, тем меньше становится давление воздуха. Этим можно воспользоваться для того, чтобы с помощью барометра определять высоту подъема. Как показывают расчеты, при постоянной температуре воздуха разность высот двух точек выражается такой формулой:
346
Здесь р1 и р2 - давление воздуха на высотах h1 и h2, р0 - давление воздуха на уровне моря, W0 - вес 1 м³ воздуха при температуре 0° и давлении р0, t0 - температура воздуха.
Эта формула верна для не слишком больших высот.
Исследования, проведенные в Советском Союзе по программе Международного геофизического года при помощи ракет, показали, что на больших высотах имеют место другие законы изменения давления с высотой.
Вообще любая физическая формула имеет ограниченную область применения - она верна при одних условиях и перестает быть верной при других. Дело в том, что при выводе любой физической формулы делаются некоторые допущения, верные лишь приблизительно. Когда же эти допущения перестают быть верными, формула теряет силу.
Много трудных математических задач приходится решать в теории межпланетных путешествий. Одной из них является задача об определении количества топлива, необходимого для того, чтобы придать ракете нужную скорость v. Это количество М зависит от массы m самой ракеты (без топлива) и от скорости v0, с которой продукты горения вытекают из ракетного двигателя.
Если пренебречь сопротивлением воздуха и притяжением Земли, то количество топлива определится формулой:
M = m ( ev/v0 - l)
(формула К. Э. Циолковского). Например, для того чтобы ракете с массой 1,5 т придать скорость 8 км/сек, надо при скорости истечения газов 2 км/сек взять примерно 80 т топлива.
Если бы удалось увеличить скорость истечения газов до 4 км/сек, то понадобилось бы всего 10 т топлива. Вообще чем с большей скоростью v0 вытекают газы из ракеты, тем меньше будет
V
ev/v0 и тем меньше понадобится топлива. Другой
способ уменьшения количества топлива заключается в замене одноступенчатых ракет многоступенчатыми (подробнее о ракетах см. в статьях т. 3 и 5 ДЭ).
Мы рассмотрели несколько примеров из физики и техники, в которых так или иначе встречается показательная функция. Сейчас перейдем к рассмотрению примеров, связанных с тригонометрическими функциями.
Начнем с гармонических колебаний. Возьмем, например, гирю, подвешенную на пружине, и толкнем ее вниз. Гиря начнет колебаться вниз и вверх. Как показывают расчеты, отклонение гири от положения равновесия выражается формулой
s =( v0 / w) sin w t.
Здесь v0 - скорость, с которой мы толкнули
гирю, а w = √‾(k/m}, где m - масса гири и к -
жесткость пружины (сила, которая нужна, чтобы растянуть пружину на 1 см).
Колебания, происходящие по закону
s=Asin w t, (1)
называют синусоидальными или гармоническими, а график функции (1) - синусоидой. Мы можем получить представление о таких колебаниях, следя за движением равномерно вращающейся точки и наблюдая это движение одним глазом сбоку (так, что глаз наблюдателя находится в плоскости вращения). Нам будет казаться, что точка не вращается, а движется то в одну сторону, то в другую. Такую картину наблюдают астрономы, следя за движением спутников Юпитера, когда Земля находится в плоскости орбиты этих спутников.
Число А, называемое амплитудой синусоидального колебания, показывает размах этого колебания, а число w, называемое частотой колебания, показывает, сколько колебаний происходит за 2 p секунд (т. е. примерно
за 44/7 секунды). Через каждые 2 p / w секунды гиря
будет возвращаться в исходное положение. Поэтому период ее колебания равен 2 p / w .
Если мы сначала оттянем гирю на s0 см, а потом толкнем ее со скоростью v0, то она будет совершать колебания по более сложному закону:
s= A sin ( w t+ a). (2)
347
Расчеты показывают, что амплитуда А этого колебания равна √‾(s²0 +v² 0 / w²), а число a таково, что tg a = s0 w /v0, Из-за слагаемого а это колебание отличается от колебания s=Asin w t. На рисунках 7 и 8 изображены графики обоих колебаний. График колебания (2) получается из графика колебания (1) сдвигом влево на
a / w. Число a называют начальной фазой.
со
Рис. 7. График гармонического колебания.
Рис. 8. График колебательного движения с начальной фазой.
Колебания маятника тоже приближенно происходят по синусоидальному закону. Если эти колебания малы, то угол отклонения маятника приближенно выражается формулой:
где l - длина маятника, а j0 - наибольший угол отклонения. Чем длиннее маятник, тем медленнее он качается. Измеряя период колебания маятника известной длины, можно вычислять ускорение земного тяготения g в различных точках земной поверхности.
Не только многие механические колебания происходят по синусоидальному закону. И в электрических цепях возникают синусоидальные колебания. Замкнем, например, цепь, изображенную на рис. 9. Ток в этой цепи будет изменяться по синусоидальному закону:
I = I0 sin( w t + a). Частота w колебаний тока равна 1/ √‾LC, где С- емкость конденсатора, a L - самоиндукция цепи. Этот закон очень похож на закон колебаний гири, только вместо жесткости пружины надо взять величину, обратную емкости конденсатора, а вместо массы гири - самоиндукцию катушки.
Приведенные примеры могут создать впечатление, что синусоиды встречаются только в связи с колебаниями. Однако это не так. Например, синусоиды используются при соединении двух цилиндрических труб под углом друг к другу. Чтобы соединить две трубы таким образом, надо срезать их наискосок. Если развернуть срезанную наискосок трубу, то она окажется ограниченной сверху синусоидой. В этом можно убедиться, обернув свечку бумагой, срезав ее наискосок и развернув бумагу. Поэтому, чтобы получить ровный срез трубы, можно сначала обрезать металлический лист сверху по синусоиде и свернуть его в трубу.
Синусоида встречается при рассмотрении изгиба колонны под действием вертикальной нагрузки. Если нагрузка слишком мала, колон-
348
на не изгибается совсем. Но если нагрузка достигнет некоторого значения, называемого критическим, то колонна начнет изгибаться, причем ее ось примет форму синусоиды. В этом можно убедиться на опыте, сгибая вместо колонны металлическую линейку. Критическая сила равна:
F= p² EI/l²,
где l - высота колонны, а числа Е и I зависят от материала колонны и размеров ее сечения. Из формулы видно, что чем длиннее колонна, тем меньшая сила нужна, чтобы ее согнуть. Это также можно проверить, изгибая линейку.
Формула критической силы была открыта Л. Эйлером.
До сих пор, говоря о колебаниях маятника, гири, качающейся на пружине, и т. д., мы пренебрегали сопротивлением воздуха. На самом деле из-за сопротивления воздуха амплитуда колебаний становится все меньше и меньше, колебания затухают. Отклонение точки, совершающей затухающие колебания, выражается такой формулой:
s= Ае- kt sin ( w t+ a).
Так как множитель е-kt уменьшается с течением времени, то размах колебаний становится все меньше и меньше. После каждого полного
колебания амплитуда уменьшается в е раз.
Число 2 p / w называют логарифмическим декрементом затухающего колебания. Чем больше логарифмический декремент, тем быстрее затухают колебания. Через некоторое время они станут такими маленькими, что приборы покажут полную остановку тела. График затухающего колебания изображен на рис. 10.
Если сопротивление среды очень большое (скажем, если маятник качается не в воздухе, а в масле), то колебаний не будет совсем - выведенный из положения равновесия маятник медленно будет опускаться, приближаясь к положению равновесия. В этом случае закон его движения задается формулой вида:
s = А1 е-k1t +A2 e-k2t,
где числа А1 и А2 зависят от начального положения и начальной скорости маятника.
При электрических колебаниях также происходят затухающие колебания из-за наличия сопротивления цепи.
Рассмотрим снова гирю, качающуюся на пружине. Если не мешать ей качаться, то она будет совершать колебания с определенной частотой w. Эта частота называется собственной частотой колебания гири. Совсем по-другому будут выглядеть колебания гири, если мы будем раскачивать ее. Пусть раскачивающая сила сама изменяется по синусоидальному закону, т. е. тащит гирю то вверх, то вниз. Тогда гиря будет совершать колебания, получающиеся при сложении двух колебаний. Одно из них происходит с собственной частотой колебания гири, а второе - с частотой раскачивающей силы. Пусть в начале колебания гиря находится в состоянии покоя и раскачивающая сила изменяется по закону: F=Asin b t. Тогда закон движения гири выразится формулой:
где w - собственная частота колебаний гири. График пути гири имеет уже довольно сложный вид. Дело в том, что функции sin b t и sin w t меняются с разной частотой. Поэтому иногда два колебания, в которых участвует гиря, направлены в разные стороны (так будет, например, в начале колебания) и гасят друг друга. Иногда же они направлены в одну сторону, и тогда они усиливают друг друга.
Наибольшая амплитуда колебания равна
примерно │ A/( w ( w - b)) │. Отсюда видно, что если [3
Рис. 10. График затухающего колебания.
349
мало отличается от w (т. е. если частота раскачивающей силы мало отличается от собственной частоты колебаний гири), то амплитуда колебаний может стать очень большой (у дроби
│ A/( w ( w - b)) │ знаменатель будет маленьким). Если
w = b (т. е. если мы раскачиваем гирю в такт ее собственным колебаниям), то формула (3) уже неприменима. В этом случае закон движения гири имеет вид:
s=(A/2 w²)[sin w t- w t cos w t].
Размах колебаний с течением времени увеличивается, и гиря может разорвать пружину. Это явление называют резонансом.
Иногда одно и то же тело участвует не в одном колебательном движении, а в нескольких. Подвесим, например, гирю А на пружине, а к ней также на пружине подвесим другую гирю В (рис. 11). Если растянуть обе пружины и отпустить их, то колебания гирь А и В будут весьма сложными. Например, колебания гири В вызываются, во-первых, тем, что гиря А то поднимается, то опускается, и, во-вторых, тем, что пружина АВ то растягивается, то сокращается. Мы говорим в этом случае, что колебание гири В является суммой двух колебаний - движения гири А и колебания гири В относительно гири А. Можно привести и другие примеры сложения колебаний. Когда играет оркестр, то каждый музыкальный инструмент вызывает свои колебания воздуха. Эти колебания складываются друг с другом и доносятся к нам в виде единого аккорда.
Чаще всего складываются гармонические колебания. Если эти колебания имеют одну и ту же частоту, то и сумма их будет гармоническим колебанием той же частоты. Для сложения колебаний можно пользоваться простым геометрическим правилом. Здесь нам приходят на помощь векторы. (Подробнее о векторах см. в статье «Алгебра векторов».) Оказывается, что не только силу, скорость и ускорение, но и гармонические колебания можно изображать векторами.
Гармоническое колебание с амплитудой А и начальной фазой а изображают вектором длины A, наклоненным к оси Ох под углом а (рис. 12). При сложении колебаний изображающие их векторы складываются по правилу параллелограмма. На рис. 13 показано сложение колебаний:
s1 =10 sin w t и s2 =6 sin( w t+ p /3).
Измеряя диагональ О B параллелограмма ОАВС, находим, что амплитуда суммы этих колебаний равна примерно 14. Начальная же фаза этого колебания равна углу АОВ, т. е. примерно 22°, или 0,37 радиана. Поэтому:
s = 10sinωt + 6sin(ωt+π/3) ≈ 14sin(ωt+0,37).
Особенно просто складывать колебания с одинаковой начальной фазой - в этом случае оба вектора направлены в одну сторону и в, сумме получится колебание с той же фазой, амплитуда которого равна сумме амплитуд слагаемых. А если углы a1 и a2 отличаются друг от друга на p радиан (т. е. на 180°), то в результате сложения получится колебание, амплитуда которого равна разности амплитуд слагаемых. Может получиться даже, что колебания погасят друг друга (одно будет тянуть в одну сторону, а другое - в другую, совсем как Лебедь, Рак. и Щука из басни Крылова). Такое явление называют в физике интерференцией колебаний. Из-за интерференции может получиться так, что точка, освещенная двумя источниками света, окажется неосвещенной - два света дадут в сумме темноту.
Довольно сложная картина возникает, когда складываются колебания различной частоты. При этом уже получаются несинусоидальные колебания. Если частоты w1 и w2 складываемых колебаний близки друг к другу, то; получающееся колебание имеет вид как бы си-
350
нусоидального колебания с частотой ( w1 + w2)/2 ,
амплитуда которого медленно меняется с часто-
той │ ( w1 - w2)/2 │. Это явление называют биениями. Может случиться, что мы не воспринимаем слагаемых колебаний из-за того, что их частота слишком велика, но можем воспринять медленное изменение амплитуды суммы колебаний. Например, если электрическая лампочка присоединена к динамо-машине, дающей переменный ток с периодом Т = 1/50 сек., то изменения в яркости лампочки будут незаметными. Если же присоединить эту лампочку к двум динамо-машинам, периоды которых мало отличаются друг от друга, то возникнут биения и лампочка начнет мигать.
Возникают биения и на двухвинтовом корабле, если винты имеют близкие, но различные периоды вращения. Приходится учитывать биения и композиторам. Колебания с периодически меняющейся амплитудой применяют в радиотехнике. Радиостанции посылают в пространство электромагнитные колебания с очень большой частотой (от 150 тыс. до 15 млн. колебаний в секунду). Амплитуда же этих колебаний меняется примерно со звуковой частотой (несколько сотен или тысяч колебаний в секунду). Такого изменения амплитуды можно добиться, вызвав биения. Этот прием называют частотной модуляцией.
Очень интересный пример биений дают океанские приливы и отливы. Из-за притяжения Луны и Солнца уровень воды в океане все время меняется. Примерно каждые 12 час. уровень воды достигает наивысшего значения, а через 6 час. после этого - наинизшего. Однако из-за вращения Луны вокруг Земли период колебаний уровня воды, вызываемых притяжением Солнца, не совпадает с периодом колебаний уровня воды, вызываемых притяжением Луны. Первый период равен 12 час., а второй - 12 час. 25 мин. В результате сложений этих колебаний, имеющих близкие периоды, получаются биения. Самая большая и самая малая высота приливов будет в том случае, если Солнце, Земля и Луна расположены так, как показано на цветной вклейке на стр. 352-353. Самая большая высота приливов превосходит примерно в 2 1/3 раза самую малую.
Как мы узнали, из гармонических колебаний составляются более сложные колебания. При этом могут получаться колебания весьма сложного вида.
Оказалось, что любое самое сложное периодическое колебание можно изобразить как сумму синусоидальных колебаний (т. е. таких, что их графики имеют форму синусоиды). Частоты этих синусоидальных колебаний называют спектром сложного колебания, а само разложение - спектральным анализом колебания.
Это название не случайно. Разложение луча света в спектроскопе связано с разложением сложного электромагнитного колебания на простые синусоидальные составляющие.
Спектральный анализ применяют также к звукам и другим колебаниям. С помощью спектрального анализа удается установить особенности тембра голоса певца и т. д.
В технике пользуются спектральным анализом колебаний для того, чтобы правильно рассчитывать различные конструкции. Например, может случиться, что частота одной из синусоидальных составляющих колебаний самолета, вызванных работой моторов, совпадет с собственной частотой колебаний какой-нибудь детали самолета. Тогда из-за резонанса при работе моторов возникнут сильные колебания этой детали, что может привести к аварии.
Для разложения периодических колебаний на синусоидальные составляющие применяют различные машины. Есть машины, которые
351
решают и обратную задачу - позволяют из синусоидальных составляющих складывать все колебание. Однажды для проверки работы такой машины ей дали разложить на синусоидальные составляющие колебание, изображенное на рис. 14, а потом сложить эти составляющие. Машина после суммирования начертила график не такой, как на рис. 14, а такой, как на рис. 15, т. е. с добавочными хвостиками на вертикальных отрезках. Сначала появление этих хвостиков приписывали несовершенству машины и думали, как ее исправить. Но потом американский физик Дж. Гиббс доказал, что эти хвостики должны появляться всегда, когда у графика колебания есть разрыв. Теорему назвали его именем, хотя «открыла» ее машина.
Почему не работал трансатлантический кабель
Когда проложили телеграфный кабель через Атлантический океан, то оказалось, что по нему нельзя передавать телеграммы. Вместо точек и тире на другом конце кабеля принимались совершенно непонятные сигналы. Исследованием работы кабеля занялся известный английский физик и математик Кельвин. Для этого он сначала разложил сигналы на синусоидальные составляющие и изучил, как передаются по кабелю эти составляющие. Оказалось, что колебания различной частоты передаются по-разному. Одни из них идут быстрее, другие медленнее, одни сильно ослабевают, а другие меньше. Поэтому, когда эти составляющие приходят на другой конец кабеля, то их сумма становится совсем непохожей на передававшиеся сигналы. Кельвин нашел, от чего зависит изменение скорости и силы синусоидальных колебаний, и указал, как сделать кабель, чтобы колебания любой частоты шли по нему с одинаковой скоростью и одинаково ослабевали. Когда по его указаниям переделали кабель, сигналы стали передаваться без искажений и трансатлантическая связь наладилась.
Иногда вместо разложения колебания на синусоидальные составляющие стараются выделить из всего колебания одну составляющую определенной частоты. Именно это делают, когда настраивают радиоприемник на определенную частоту; из сложного электромагнитного колебания, вызванного работой всех радиостанций, ловят колебание, вызванное работой нужной станции. Точно так же камертон отзывается только на ту ноту, на которую он настроен.
Поистине безгранична область применений показательной и тригонометрической функций в природе и технике! Вероятно, можно было бы заполнить весь этот том, рассказывая о таких примерах. Возникают естественные вопросы: Что общего между такими вещами, как трение каната о столб, радиоактивный распад, остывание чайника? Почему электромагнитные колебания так похожи на механические колебания? Почему столь часто встречаются в различных вопросах науки и техники именно эти функции?
Сейчас мы не можем ответить на эти вопросы. Но в конце следующей статьи, посвященной одному из разделов высшей математики, поговорим и об этом.
На одном конце кабеля передавали сигналы.
На другом конце кабеля получали сигналы, которые нельзя было понять.
352
Как сожмется пружина, если под колесо автомобиля попадет камень? Ответ на этот вопрос может дать физическая модель, состоящая также из пружины, грузов а т. д., или математическая модель, которая представляет собой электрическую цепь из катушек самоиндукции, конденсаторов, реостатов и т. д.
В декабре 1887 г., на юге Индии, в бедной семье родился мальчик - Сриниваза Раманужан. В школу он пошел вместе со своими сверстниками, но постепенно всех их обогнал в успешном изучении математики, проявляя при этом поразительную самобытность и оригинальность мышления. К концу седьмого года обучения в школе он уже приобрел хорошие знания по алгебре и тригонометрии и приступил к изучению высшей математики. В том селении, где учился Раманужан, нашлась единственная книга по высшей математике, содержащая 6165 теорем и формул, большая часть которых дана в книге без доказательств и выводов. Раманужану приходилось самому изобретать методы доказательств и способы решения задач, изложенных в книге и возникавших в его голове. Тетради, в которые юноша Раманужан заносил свои мысли, выводы и вычисления, были впоследствии даже изданы.
В 16 лет Раманужан окончил школу и был зачислен в колледж при Мадрасском университете, но проучился там только год.
Поддерживая свое существование малоинтересной случайной работой, Раманужан все свободное время отдавал математическому творчеству, заполняя тетрадку за тетрадкой своими виртуозными вычислениями и изысканиями.
Так прошло 10 лет. Однажды по совету друзей Раманужан послал несколько кратких сообщений о своих результатах известному английскому математику Г. Харди. Ученый высоко оценил незаурядное дарование Раманужана, добился его зачисления в Кембриджский университет (1914) и сам руководил его занятиями.
Весной 1917 г. Раманужан заболел, и болезнь перешла в открытую форму туберкулеза, но он не переставал работать даже в больницах и санаториях.
В ноябре 1918 г. Раманужан был избран членом Лондонского королевского общества и профессором Кембриджского университета.
В январе 1919 г. Раманужан выехал на родину, но приехал в Индию в плохом состоянии и 26 апреля 1920 г. умер, на 33-м году жизни.
Взгляните - вот одно из многих тождеств, открытых школьником Раманужаном:
где n - любое целое положительное число. Три точки между знаками «+» означают, что промежуточные слагаемые подразумеваются как очевидные. Если принять, например, n =5, то первое слагаемое левой суммы будет 1/( n+1) =1/6, предпоследнее слагаемое 1/2 n=1/10, последнее слагаемое - n/(2n+1) =-5/11. первое слагаемое правой суммы 1/(2³ -2), а последнее 1/(10³ -10) и тогда
1/6+1/7+1/8+1/9+1/10-5/11=1/(2³ -2)+1/(4³ -4)+1/(6³ -6)+1/(8³ -8)+1/(10³ -10).
Произведите вычисления - и вы убедитесь в правильности тождества Раманужана для n =5. Но доказать, что это равенство правильно для любого целого положительного числа - далеко не легкая задача. Попытайтесь, кто хочет.
Проверьте справедливость курьезных равенств:
1=1·1/1;
12=22·22/(1+2+1);
12321= 333·333/(1+2+3+2+1);
1234321=4444·4444/(1+2+3+4+3+2+1).
Исследуйте самостоятельно, как далеко распространяется эта легко наблюдаемая закономерность.
Любопытные прямоугольные треугольники
Интересно, что существуют только два прямоугольных треугольника с целочисленными сторонами, площадь каждого из которых численно равна периметру. Вот один: а =6, b =8, с=10. А второй найдите!
Ответ на стр. 373.
Запись: 121 имеет смысл числа не только в десятичной системе, но и в любой другой, основание которой B>2. Это число интересно тем, что является полным квадратом как при
основании 10 (121 = 11²), так и при любом другом основании B >2.
Докажите! Решение на стр. 373.
Напишите какое хотите дробное или целое число, кроме 0 и 1. Отнимите его от 1. Напишите число, обратное получившейся разности, и повторите с новым результатом весь цикл указанных действий. После третьего раза непременно получится то число, с которого начинали.
- Неужели так будет с любым числом?
- Да, и это легко доказать (см. стр. 373).
353
Если бы бочки умели говорить, то, несомненно, многие из них с удовольствием рассказали бы поучительную историю о великих заслугах бочек в создании ... высшей математики! История эта такова.
В ноябре 1613 г. королевский математик и астролог австрийского двора И. Кеплер праздновал свадьбу. Готовясь к ней, он приобрел несколько бочек виноградного вина. При покупке Кеплер был поражен тем, что продавец определял вместимость бочки, производя одно-единственное действие - измеряя расстояние от наливного отверстия до самой дальней от него точки днища (рис. 1). Ведь такое измерение совсем не учитывало форму бочки! Кеплер сразу увидел, что перед ним интереснейшая математическая задача - по нескольким измерениям вычислить вместимость бочки. Размышляя над этой задачей, он нашел формулы не только для объема бочек, но и для объема самых различных тел: лимона, яблока, айвы и даже турецкой чалмы. Для каждого из тел Кеплеру приходилось создавать новые, зачастую очень хитроумные методы.
В наши дни вычислять объемы различных тел (значительно более сложных, чем у Кеплера) необходимо при решении многих технических задач: при нахождении объема корпуса корабля, объема газгольдера, объема водохранилища и др. И решать такие задачи приходится почти каждому инженеру, каждому технику. Простые и общие методы решения подобных задач даются высшей математикой.
Чтобы получить представление об этих общих методах, попробуем найти объем поданного к столу лимона. Ни на одно из тел, изучаемых в школе (шар, цилиндр, конус и т. д.), лимон непохож. Однако хозяйка тут же приходит нам на помощь: она разрезает лимон на тонкие ломтики. Ровно обрезав край каждого ломтика, можно превратить его в низенький цилиндр (рис. 2), объем которого легко высчитать. Прикладывая друг к другу эти цилиндры, мы получим ступенчатое тело (рис. 3). Его объем равен сумме объемов цилиндров. Если ломтики очень тонки, то объем ступенчатого тела мало отличается от объема лимона, и чем тоньше будут ломтики, тем это отличие будет меньше.
Прием, примененный нами для вычисления объема лимона, пригоден для вычисления объема любого тела вращения. Пусть фигура ABCD (рис. 4) вращается вокруг стороны АВ. Разрежем получающееся тело вращения (рис. 5) на тонкие ломтики и каждый ломтик заменим цилиндром. Тогда легко сможем найти объем
354
получающегося ступенчатого тела (рис. 6). Для этого надо знать, как меняется площадь сечения с высотой (рис. 7). Пусть площадь сечения, проведенного на высоте h, равна S(h). Предположим, кроме того, что тело разрезано на n ломтиков сечениями, проведенными на высотах h0, h1 ,..., hn над плоскостью нижнего основания (плоскость нижнего основания совпадает с сечением на высоте h0, а плоскость верхнего - с сечением на высоте hn, т. е. h0 =0, hn =H (см. рис. 6). Площадь сечения на высоте hk равна S(hk). Поэтому объем цилиндра, которым мы заменяем k -й ломтик (рис. 8), будет равен S ( hk)( hk -hk -1) (так как его высота равна hk -hk -1). Складывая объемы цилиндров, получим объем всего ступенчатого тела:
V ступ. тела = S(h1) ( h1 - h0)+ S ( h2) (h2 - h1) +...+ S ( hn)( hn -hn-1).
Чем тоньше будут ломтики, тем ближе объем ступенчатого тела к объему тела вращения.
Таким же образом можно найти объем любого тела, если известно, как меняется площадь тела с высотой сечения. Например, для того чтобы вычислить объем проектируемого корабля, достаточно иметь чертежи (выполненные в определенном масштабе) поперечных разрезов корабля. По этим чертежам надо найти площадь каждого разреза (как вычислять площади сложных фигур, мы расскажем ниже), после
чего указанная выше формула даст приблизительное значение объема корабля. Разумеется, таким же приемом можно находить объемы газгольдеров, водохранилищ и других тел.
При проектировании гидроэлектростанций надо знать расход воды в реке, т. е. количество воды, протекающей в данном месте за 1 сек. Ясно, что расход воды в реке равен произведению площади поперечного сечения реки на скорость течения. Скорость течения определить довольно просто, а вот площадь поперечного сечения найти гораздо сложнее. Однако и здесь на помощь нам приходит разрезание на «ломтики». Каждый «ломтик» можно приближенно заменить прямоугольником. Складывая затем площади этих прямоугольников, мы и найдем приближенное значение площади сечения. Чем тоньше будут «ломтики», тем более точное значение площади мы получим. Измерим глубину реки в точках, находящихся на расстоянии x0 , x1 , ...,хn от берега (х0 =0; хn =Н - ширина реки). Пусть на расстоянии xk от берега глубина равна f(xk) (рис. 9). Тогда площадь поперечного сечения приблизительно равна
Sпопер. сеч. ≈ f (x1) ( x1 - x0)+ f ( x2) ( x2 - x1) +... + f(xn)( xn -xn -1).
Вообще если геометрическая фигура имеет вид, изображенный на рис. 10 (такая фигура
355
называется криволинейной трапецией), и если высота в точке с абсциссой х равна f ( x), то для вычисления площади фигуры мы можем пользоваться той же формулой. Чем гуще расположены точки х0 , x1,..., хп на отрезке АВ, тем более точное значение для площади фигуры получим по этой формуле.
Для измерения пути, пройденного автомобилем, на нем устанавливают специальный счетчик. Но даже если этот счетчик испорчен, можно подсчитать пройденный автомобилем путь по спидометру (прибору, показывающему скорость автомобиля). Для этого надо записать показания спидометра в моменты времени t0 = 0, t1, t2 ,..., tn =T . Если бы движение автомобиля от момента tk -1 до момента tk совершалось равномерно с той скоростью v(tk), которую он в действительности имел в конце этого промежутка, т. е. в момент tk, то за промежуток времени от tk -l до tk он проехал бы расстояние v ( tk)( tk - tk -1). Поэтому путь, пройденный за все время движения от 0 до Т, был бы равен:
v ( t1)( tl -t0) + v ( t2)( t2 -t1) +... + v ( tn)( tn - tn -1).
Этой формулой можно пользоваться для приближенного подсчета пути, пройденного автомобилем. Но автомобиль не всегда движется равномерно, и даже за маленький промежуток времени скорость его успевает несколько раз измениться. Однако чем чаще будем записывать показания спидометра, т. е. чем меньше будут промежутки времени между отдельными измерениями, тем точнее написанная формула будет давать пройденный автомобилем путь.
Мы разобрали ряд задач из различных областей физики, техники, геометрии. Несмотря на внешнее различие этих задач, у них было много общего. Каждый раз для приближенного вычисления некоторой величины (объема, площади, пути и т. д.) мы получали сумму вида:
Здесь f(x) - некоторая функция, заданная на отрезке от а до b , а х0 =а, х1 ..., хп-1, хп = b - точки на этом отрезке. Например, при вычислении пути функция f(x) была скоростью в момент времени х (только время мы раньше обозначали буквой t, а не х, что, конечно, несущественно), а было равно нулю, а b равнялось времени Т движения автомобиля.
Суммы такого вида встречаются в математике и ее приложениях очень часто. Их называют интегральными суммами. Такие суммы дают значение искомой величины только приближенно. Но если мы будем брать точки х0 , х1 ,..., хn все гуще и гуще на отрезке от а до b , то интегральные суммы будут приближаться к некоторому числу, а именно к точному значению искомой величины. Это число называется интегралом от функции f(x) на от-
резке от а до b и обозначается через
Таким образом,
где предел lim берется при условии, что число промежутков неограниченно увеличивается, а их длины стремятся к нулю.
В самом обозначении
сохраняются воспоминания об интегральной сумме, из которой получается интеграл. В Италии букву 5 часто пишут в виде ∫. Поэтому сам знак интеграла есть просто первая буква латинского слова Summa (сумма). Вслед за знаком [ указывается, что суммировались выражения f ( xk)( xk -xk -1). Только вместо разности xk -xk -1 пишут dx, где d - первая буква латинского слова differentia (разность). Понятие интеграла является одним из основных в математике. Пользуясь этим понятием, можно записать многие полученные
356
ранее формулы гораздо короче и не приближенно, а точно. Например, формула объема любого тела принимает вид:
где Н - высота этого тела, a S(h) - площадь сечения, проведенного параллельно основанию тела на высоте h от основания (см. рис. 7).
Формулу площади фигуры, изображенной на рис. 10, можно записать в виде:
где f(x) - высота кривой CD в точке с абсциссой х.
Путь, пройденный за промежуток времени от 0 до Т, выражается через скорость v(t) по формуле:
Формулы (1) и (2) можно использовать для нахождения площадей и объемов различных тел. Но так как площади и объемы простых тел мы уже знаем, то, наоборот, с помощью этих формул можно вычислить значения некоторых простых интегралов. (Дальше, на стр. 368, мы укажем, как можно сосчитать эти интегралы непосредственным вычислением, не прибегая к геометрии.)
Самой простой геометрической формулой вычисления площади является формула площади прямоугольника: S=hb. Прямоугольник можно рассматривать как криволинейную трапецию, высота которой во всех точках одинакова
и равна h (рис. 11), так что его площадь может
быть записана в виде интеграла:
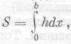 где h - постоянная величина. Итак, мы доказали формулу:
где h - постоянная величина. Итак, мы доказали формулу:
(h - постоянная). В частности, при h= 1 получаем:
Вспомним теперь формулу площади прямоугольного треугольника: S =1/2 hb, где h и b -
катеты. Из рис. 12 видно, что треугольник можно рассматривать как криволинейную трапецию,
высота у которой в точке с абсциссой х равна hx/b (это вытекает из подобия треугольников
ОАВ и OCD). Поэтому площадь треугольника может быть записана в виде интеграла:
Таким образом, мы доказали, что
Если треугольник ОАВ равнобедренный, т. е. если h=b, то получаем формулу:
Наконец, рассмотрим еще один пример. Возьмем правильную четырехугольную пирамиду с ребром в основании, равным b , и высотой, равной этому ребру (рис. 13). Поставим
357
пирамиду на вершину (так, чтобы ось ее была вертикальной) и проведем плоскость параллельно основанию пирамиды на расстоянии х от вершины. Тогда в сечении получится квадрат
со стороной, тоже равной х, а площадь его S (х) будет равна x². Поэтому по формуле (1) объем V пирамиды выразится интегралом:
Сравнивая эту формулу с известной из школьного курса формулой объема пирамиды, получим:
или:
Найденные выше формулы (5), (6), (7), очевидно, можно объединить в одну общую формулу:
при n =0, 1, 2.
Эта формула, как доказывается в математике, справедлива не только при n = 0, 1, 2, но и при любых положительных значениях показателя n , например:
Теперь уже нетрудно научиться вычислять интеграл от любого многочлена. Сделаем предварительно два простых, но очень важных замечания.
Первое замечание. Пусть два тела М1 и М2 движутся в одном и том же направлении, причем так, что скорость тела М2 в каждый момент времени в k раз больше скорости тела М1. Тогда ясно, что и путь, пройденный телом M2, будет в k раз больше пути, пройденного за то же время телом M1. Запишем этот очевидный факт формулой. Обозначим скорость тела M1 в момент t через v(t), тогда скорость тела М2 в тот же момент равна kv(t). Пути s1 и s2, пройденные телами М1 и M2 за промежуток времени от t =0 до t=T, равны следующим интегралам:
Но так как путь, пройденный вторым телом, в k раз больше пути, пройденного первым телом (т. е. s2 =ks1), то
Иначе говоря, числовой (постоянный) множитель можно выносить из-под знака интеграла.
Второе замечание. Пусть тело М1 движется в некотором направлении, а по его поверхности движется в том же направлении тело М2. Например, баржа плывет по реке, а по ее па-
358
лубе идет человек. Обозначим скорость движения тела M1 через v1 ( t), а скорость перемещения тела М2 по поверхности тела М1 - через v2 ( t). Тогда путь, пройденный телом М1 за время от t =0 до t=T, равен
а путь, пройденный телом M2 по поверхности тела М1, равен
Общий же путь, пройденный в пространстве телом M2 (как за счет собственного движения, так и за счет движения тела М1, которое его везет), равен
Но ясно, что скорость перемещения тела М2 в пространстве равна v1 ( t) +v2 ( t), так что путь, пройденный этим телом, имеет значение:
Приравнивая оба найденных значения пути, получим:
т. е. интеграл от суммы двух (или нескольких) функций равен сумме интегралов от слагаемых.
Переходим к интегрированию многочленов. Пусть, например, нужно вычислить интеграл
Так как подынтегральное выражение есть сумма х² + (-3 x)+5, то можно наш интеграл разбить на три:
Во втором и третьем интегралах можно вынести за знак интеграла числовой множитель, после чего легко получим ответ:
Иначе говоря, интегрировать многочлены можно почленно. Вообще, если
f ( х) =а0 хn +а1 xn-1 +...+ an -l x + аn -
некоторый многочлен n - й степени, то его интеграл находится по формуле:
Мы научились вычислять интегралы от многочленов. Этого уже достаточно, чтобы иметь возможность решать многие математические и физические задачи.
Покажем для начала, как просто получаются с помощью интегралов некоторые формулы, изучаемые в школе.
Выведем формулу пути равноускоренного движения. Если начальная скорость тела в момент t =0 равна v0, а ускорение движения равно а, то в момент времени t скорость тела составит v(t)=v0 + at. Поэтому по формуле (3)
359
путь, пройденный телом с начала движения до момента Т, выражается формулой:
Выведем теперь некоторые геометрические формулы. Сначала найдем, чему равен объем шара радиуса R. Конечно, нам достаточно найти объем полушара, а потом его удвоить. Рассечем полушар плоскостью, параллельной его основанию и отстоящей на х от основания (рис. 14). В сечении получится круг радиуса АВ = √‾(R² -х²) (это получается, если применить теорему Пифагора к треугольнику ОАВ). Поэтому площадь получившегося сечения равна:
p (( √‾ ( R² -x²)²)= p R² - p x² .
Но тогда объем полушара (высота его равна R) выражается формулой:
Следовательно, объем всего шара равен
4/3 p R³ .
Но с помощью интегрального исчисления можно найти и такие площади и объемы, которые не изучаются в школе. Найдем, например, площадь параболического сегмента АОВА, у которого хорда АВ равна b , а стрелка ОС равна h (рис. 15). Уравнение параболы имеет
вид y =а x². В точке с абсциссой х= b/2 ордината AD должна равняться длине стрелки h.
Поэтому h = ab² /4. Но это значит, что а 4 h/b² .
Итак, наш параболический сегмент ограничен снизу параболой, у которой в точке с абсциссой х ордината у=4 hx² /b² .
Мы легко можем теперь найти площадь криволинейного треугольника ОА D .
По формуле (2) она равна:
Площадь же прямоугольника ABED равна bh. Но площадь параболического сегмента получается, если из площади прямоугольника вычесть удвоенную площадь треугольника
OAD, т. е. она равна 2 bh /3 .
Круговой сегмент, имеющий небольшой центральный угол, можно приближенно заменить параболическим сегментом с той же хордой и той же стрелкой (рис. 16). Поэтому для площади кругового сегмента имеет место приближенная формула:
Sкруг. сегм. ≈ 2/3 bh.
Например, если центральный угол равен 60°, то приближенная формула дает результат
360
0,0893... R², а точная 0,0906... R². Таким образом даже для такого сравнительно большого центрального угла, как 60°, приведенная формула дает точность до 1,5%.
Тот же прием, который мы применили для приближенного вычисления площади кругового сегмента, можно, конечно, применить и для случая произвольной криволинейной трапеции, ограниченной сверху кривой CD с уравнением y=f ( x) (рис. 17). Обозначим через М
середину отрезка АВ и восставим в точках А, М и В ординаты AD, MN, ВС кривой CD. Длины этих ординат обозначим через у0 , у1, у2. Проведем через точки С, N и D дугу параболы, имеющей вертикальную ось (такую дугу можно провести всегда, и притом только одну; иногда она превращается в отрезок прямой).
Довольно простые подсчеты, использующие формулы (5), (6), (7), показывают, что площадь, лежащая под этой дугой параболы, равна
(( b-a)/ 6)( у0 +4y1 + y2),
где b и а - абсциссы точек В и А. Без большой ошибки можно принять, что этому же равна и площадь криволинейной трапеции ABCD, т. е. что:
Sabcd ≈ ((b-a)/6( y0 +4 y1 + y2). Поскольку площадь криволинейной трапеции выражается интегралом
то
найденная формула дает приближенное значение этого интеграла. Иными словами,
где у0 , у1 , y2 - значения функции f(x) в точках с абсциссами а, ( a+b)/2 и b .
О
Объем любого тела можно приближенно считать по такой же формуле:
где Н - высота тела, S0 - площадь нижнего сечения, S1 - площадь среднего сечения, S2 - площадь верхнего сечения. К этой формуле прибегают для приближенного вычисления объема дерева, стога, бочки и других фигур более или менее сложной формы. Замечательно, что для всех фигур, изучаемых в школе (призмы, цилиндра, пирамиды, конуса, усеченной пирамиды, усеченного конуса, шара, шарового слоя, шарового сегмента), эта формула дает не приближенный, а совершенно точный результат. Проверьте это утверждение.
Мы часто говорили о скорости движения (например, автомобиля). Мы имели формулу;
в которой v(t) означает скорость движения тела в момент времени t. Такую скорость в физике называют мгновенной скоростью. Каким же образом можно измерить мгновенную скорость движения? Если речь идет о скорости движения автомобиля, в кабине которого мы едем, то все обстоит очень просто - надо лишь посмотреть на стрелку спидометра, и мы будем знать скорость движения. Но как узнать скорость движения автомобиля, проезжающего мимо нас по улице, или скорость полета пули? Мы знаем, что существуют приборы для измерения расстояний (линейки, рулетки и др.). Приложим такой прибор к измеряемому расстоянию, и ответ сразу виден. Есть приборы и для измерения времени (часы, хронометры). Много есть и других полезных приборов. Но «скоростемеров» - приборов, которые можно было бы «приложить»
361
к движущемуся мимо нас телу, чтобы непосредственно по его показанию узнать скорость движения тела, нет. Да и как «приложить» прибор к мчащемуся мимо автомобилю или летящей пуле?
До некоторой степени нам могут помочь приборы, измеряющие расстояние и время. Эти приборы позволяют измерить путь, который пролетела пуля, и время, которое она на это затратила. Разделив путь на время, мы и узнаем скорость полета пули. Однако таким образом мы получаем лишь среднюю скорость полета пули, которая мало о чем говорит: ведь сопротивление воздуха постепенно замедляло движение пули, и потому в конце пути она летела с меньшей скоростью, чем в его начале. Поэтому для определения скорости пули в некоторой точке ее пути поступают иначе. В этой точке ставят лист тонкого материала, соединенный с часами таким образом, что они отмечают момент времени t1, когда пуля пробивает этот лист. На небольшом расстоянии от него ставят второй лист, также соединенный с часами, так что они отмечают момент t2, когда пуля его пробивает. Пусть первый лист находится на расстоянии s1 от линии огня, а второй - на расстоянии s2 (рис. 18). Тогда расстояние s2 -s1 пуля пролетает за время t2 - t1. Значит, средняя скорость полета пули за это время равна:
vср =( s2 -s1)/(t2 -t1).
Но и это измерение не дает точного значения мгновенной скорости в момент t1. Ведь воздух
тормозил пулю, когда она летела между листами, и ко второму листу пуля подлетела с несколько меньшей скоростью, чем к первому. Чтобы уменьшить влияние сопротивления воздуха на скорость пули, надо ставить листы ближе друг к другу. И чем ближе будет второй лист к первому, тем точнее измерим мы мгновенную скорость полета пули в момент t1 (мы считаем, конечно, что у нас совершенно точные часы и безукоризненные линейки). При этом чем ближе друг к другу расположены листы, тем за меньший промежуток времени t2 - t1 пролетает пуля расстояние между ними. Мы можем сказать, таким образом, что мгновенная скорость полета пули равна:
v (t1)=lim( s2 - s1)/( t2 - t1),
где предел берется при условии, что значение s2 приближается к значению s1 (или, что то же самое, при условии, что значение t2 приближается к значению t1).
Различные радиоактивные вещества распадаются не одинаково быстро.
В каком же смысле можно говорить о том, что распад происходит быстро или медленно? Как можно измерить скорость распада куска радиоактивного вещества в данный момент времени? Легко измерить среднюю скорость распада за 1 год: надо измерить количество вещества, распавшегося за 1 год, и разделить его на число секунд в году. Это и даст среднюю скорость распада, выраженную в г/сек. Однако для нахождения мгновенной скорости распада этот расчет мало пригоден - ведь в течение года количество радиоактивного вещества постепенно уменьшалось, поэтому оно распадалось все медленнее и медленнее. Чтобы поточнее определить скорость распада в данный момент времени, надо измерить среднюю скорость распада не за год, а за месяц или еще лучше за сутки, час, минуту и т. д. Каждый раз надо брать количество вещества, распавшегося за это время, и делить на число секунд в выбранном промежутке времени. Так, уменьшая промежутки времени между двумя измерениями массы вещества, мы будем приближаться к какому-то числу. Это число и даст скорость распада в данный момент времени.
362
Формулами это можно записать следующим образом. Предположим, что в момент времени t1 масса еще не распавшегося радиоактивного вещества в пробирке была равна m1, а через некоторое время, в момент t2, масса его уменьшилась (так как часть вещества превратилась в продукт распада) и стала равной m2. Таким образом, за время t2 -tl масса имевшегося в пробирке радиоактивного вещества изменилась на m2 - m1 (это число отрицательное - ведь масса нераспавшегося радиоактивного вещества с течением времени уменьшается). Отношение
( m2 - m1)/( t2 - t1) представляет собой среднюю скорость изменения массы радиоактивного вещества в пробирке за рассматриваемый промежуток времени, т. е. среднюю скорость распада. Чем меньше промежуток времени t2 -t1 тем точнее это отношение выражает мгновенную скорость распада. Мы можем сказать, таким образом, что мгновенная скорость распада u ( t1) в момент t1 равна:
u( t1)=lim( m2 - m1)/( t2 - t1) ,
где предел берется при условии, что значение t2 приближается к t1 .
Совершенно аналогично можно определить мгновенную скорость химической реакции.
Услышав такой вопрос, вы, вероятно, вспомните построение касательной к окружности и дадите утвердительный ответ. Но речь идет о касательной к любой кривой, а не только к окружности. А в школьных учебниках не только ничего не сказано о проведении касательной к любой кривой, но даже не определяется, что это такое. Нельзя, разумеется, определять касательную как прямую, имеющую с кривой лишь одну общую точку: ось параболы пересекается с ней только в одной точке (рис. 19), но вряд ли кому-нибудь придет в голову говорить, что эта ось касается параболы.
Что же такое касательная к кривой и как ее провести? Постараемся ответить на эти вопросы. Проведем через точку М, лежащую на кривой, секущую MN (рис. 20). Если теперь точку N приближать по кривой к точке М, то секущая будет поворачиваться вокруг точки
М, все более приближаясь к некоторой прямой. Эта прямая и есть касательная к кривой в точке М. Для окружности это определение касательной совпадает с обычным (рис. 21): по мере приближения точки N к точке М угол OMN приближается к прямому углу, и потому касательная к окружности перпендикулярна радиусу.
Итак, касательная - это прямая, к которой приближается секущая MN, когда точка N приближается (по рассматриваемой кривой) к точке М.
Теперь нетрудно будет описать положение касательной с помощью некоторой формулы. Для этого будем считать, что кривая АВ является графиком некоторой функции y=f(x). Обозначим ординаты точек M и N через y1 и y2, а их абсциссы - через х1 и х2. Рассматривая прямоугольный треугольник MNP с гипотенузой MN и катетами, параллельными осям координат (рис. 22), мы можем легко определить угол j, под которым секущая наклонена к оси х :
tg j = PN/MP .
Но из рис. 22 ясно, что PN = у2 -у1 , МР=х2 -х1. Таким образом,
tg j =( y2 - y1)/( x2 - x1).
363
Если теперь точка N начнет по кривой АВ приближаться к точке М, то секущая MN будет, поворачиваясь, приближаться к положению касательной, так что в пределе мы получим тангенс угла, под которым касательная наклонена к оси х :
tg a =lim ( y2 - y1)/( x2 - x1) .
Предел берется при условии, что точка N приближается к М, т. е. что значение х2 приближается к х1 .
Мы рассмотрели несколько задач из физики и геометрии. Несмотря на внешнее различие этих задач, у них было много общего. В первых двух задачах (скорость движения, скорость распада) это общее заключалось в том, что мы в обоих случаях имели скорость изменения некоторой величины: скорость движения есть скорость изменения пути с течением времени, скорость распада есть скорость изменения массы радиоактивного вещества. Но и в третьем примере мы имели некоторую скорость изменения: тангенс угла наклона касательной есть скорость изменения ординаты, когда мы перемещаемся по оси х.
Действительно, отношение ( y2 - y1)/( x2 - x1) представляет собой среднюю скорость возрастания ординаты при перемещении от точки х1 к точке х2, а предельное значение этого отношения (равное
tg a) дает мгновенную скорость изменения ординаты.
Итак, во всех рассмотренных задачах мы имели мгновенную скорость изменения некоторой величины; этим и объясняется, что при определении этих на первый взгляд очень непохожих величин получились очень похожие формулы. Чисто математически скорость изменения можно определить следующим образом. Пусть мы имеем функцию y = f ( x). Обозначим те значения, которые эта функция принимает в двух точках х1 и х2, через y1 и y2. Тогда разность y2 - y1 показывает, на сколько изменилось значение рассматриваемой функции при переходе от значения x1 к значению х2,
а отношение ( y2 - y1)/( x2 - x1) представляет собой среднюю скорость изменения функции y=f ( x) на промежутке от x1 до х2. Если теперь уменьшать этот промежуток, приближая значение x2 к x1, то мы получим в пределе мгновенную скорость изменения рассматриваемой функции в точке х1 ; она равна
lim( y2 - y1)/( x2 - x1),
где предел берется при условии, что значение x2 приближается к х1. Эта мгновенная скорость изменения называется производной от функции у = f(x) по аргументу х в точке х1 ; она обозначается через f'(x1).
В этих обозначениях явно указывается, в какой точке берется мгновенная скорость изменения (т. е. производная). Есть и другие обозначения для производной, но мы их не будем указывать. Конечно, производную можно находить в различных точках, так что производная f'(x) есть опять некоторая функция от х. Теперь ясно, что рассмотренные выше задачи из физики и геометрии могут быть сформулированы с помощью производной.
Скорость движения v(t) есть производная от пути s(t) по времени:
v(t)=s'(t). (9)
Скорость u(t) радиоактивного распада есть производная от массы радиоактивного вещества m(t) по времени:
u(t)=m'(t). (10)
Наконец, тангенс наклона касательной к графику функции y=f(x), проведенной в точке с абсциссой х, есть производная от функции f(x):
tg a │в точке х = f' ( x). (11)
364
Из сказанного выше ясно, что для решения ряда задач физики, геометрии и других наук весьма важно уметь находить производные различных функций (нахождение производных называется дифференцированием). Мы рассмотрим сейчас пример непосредственного вычисления производной.
Возьмем функцию у=х³. Отношение, которое нужно рассмотреть при вычислении этой производной, имеет такой вид:
Если теперь х2 будет приближаться к x1, то последнее выражение будет, очевидно, приближаться к значению х²1 +х²1 + х²1 = 3 x²1. Таким образом, производная от функции у = х³ имеет в точке х=х1 значение З х²1, т. е.
(х³)' │приx=x1 = 3x²1. Более кратко это записывают так: ( х³)' = 3 x².
Предоставляем читателю таким же образом найти производные от функций у=х² и у=х. Результаты получаются такие:
( х²)' = 2 х ; ( х)'=1.
Эти формулы вычисления производных объединяются, очевидно, одной общей формулой:
( хn)' = n хn -1. (12)
Для случая целого положительного значения n эту формулу можно проверить примерно таким же способом, как мы выше вычислили производную от x³. В математике доказывается, что формула (12) верна при любом п. Заметим, что производная единицы (или вообще любой постоянной величины) равна нулю. Это легко следует из формулы (12), а впрочем, ясно и без этого, так как скорость изменения постоянной, очевидно, равна нулю.
Заметим теперь, что производная обладает следующими простыми, но важными свойствами: постоянный множитель можно выносить за знак производной; кроме того, производная суммы двух (или нескольких) функций равна сумме производных от слагаемых:
[ kf ( x)]'= k · f ' ( x),
[f1 ( x) +f2 ( x) ]'=f'1 ( x) +f'2 ( x).
Справедливость этих правил легко проиллюстрировать с помощью формулы (9), при-
мерно так же, как мы сделали выше для интегралов.
Теперь уже легко можно находить производные любых многочленов, например:
Вообще, если
многочлен n -й степени, то его производная вычисляется по формуле:
Русский математик П. Л. Чебышев в своей работе «Черчение географических карт» писал, что особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека: как располагать средствами своими для достижения по возможности большей выгоды. Так, рабочий-металлист старается из куска металла получить как можно больше деталей; раскройщик на обувной фабрике старается из куска кожи выкроить как можно больше заготовок; технолог старается так расставить станки на заводе, чтобы обработка деталей заняла как можно меньше времени, и т. д.
Да и не только человеку приходится решать такие задачи. Пчелы бессознательно решают одну из таких задач - они стараются придать сотам такую форму, чтобы при заданном объеме на них шло как можно меньше воска. И хотя они не знают математики, но точно решают эту задачу (рис. 23).
Пчелам помогает решать эту задачу инстинкт. Человек же действует не по инстинкту, а по разуму. Маркс говорил, что «самый плохой архитектор от наилучшей пчелы с самого начала отличается тем, что, прежде чем строить ячейку из воска, он уже построил ее в своей голове».
И большую помощь в решении таких задач оказывает человеку ма-
365
тематика, в особенности понятие производной. Чтобы понять, как же математики решают такие задачи, рассмотрим одну из них.
Пусть перед нами квадратный кусок картона со стороной а. Из него надо сделать коробку без крышки. Вырежем по углам куска квадратики (рис. 24) и согнем по линиям, отмеченным пунктиром. У нас получилась коробка (рис. 25); но много ли в нее можно положить? Это зависит от того, какие квадратики мы вырезали из этой коробки. Если
они были очень маленькие, то коробка получится низкая (рис. 26, а) и в нее много не положишь. А если они будут слишком большие (рис. 26, б), то коробка получится слишком узкая и в нее тоже войдет довольно мало. Найдем, при какой стороне х вырезанного квадратика объем V(x) сделанной коробки будет наибольшим. Из рис. 25 видно, что V = х(а- 2 x)² = 4 x³ -4а x² +а² х. График этой функции имеет вид, указанный на рис. 27. При этом х должен лежать между 0 и a/2, так как вырезать из куска картона со стороной а четыре квадрата со стороной, большей, чем a/2, нельзя. Из рис. 27 видно, что в той точке, где значение объема наибольшее, касательная идет горизонтально, т. е. образует с осью х угол, равный нулю. Но это значит, что в этой точке производная равна нулю. Таким образом, чтобы найти значение xmax, при котором объем коробки будет самым большим, надо найти все значения ж, при которых производная функции
V (х) =4 x³ -4а x² + а² х
обращается в нуль; среди них обязательно будет и искомое значение xшах. По формуле дифференцирования многочлена находим: V' (х) =12 x² -8 ах+ а². Приравниваем производную нулю и находим
два корня: х1 = a/2, х2 = a/6 . Разумеется, корень x1 = a /2 нас не устраивает: если мы вырежем
квадраты со стороной a/2, то от листа картона ничего не останется. Значит, наибольшее значение объема получится, если за xmax примем
оставшееся значение a/6, т. е. вырежем квадраты со стороной х = a/6. Объем коробки тогда будет
равен 2а³ /27. Сделать из данного куска картона коробку большего объема невозможно.
366
Основным элементом любой строительной конструкции является балка. Прочность балки зависит от того, какую форму имеет ее поперечное сечение. Инженерные расчеты показывают, что прочность балки с прямоугольным сечением пропорциональна ширине балки а и квадрату ее высоты h. Иными словами, прочность такой балки (измеренная в некоторых единицах) равна kah², где k - коэффициент, зависящий от длины балки, материала, из которого она сделана, и т. д.
Деревянные балки приходится обычно вытесывать из круглых бревен. В связи с этим возникает задача, как из бревна, имеющего радиус R, сделать балку наибольшей прочности. На рис. 28 изображено поперечное сечение бревна. Разумеется, прочность вырезанной балки будет функцией от ширины этой балки. Но если взять ширину слишком большой (почти равной диаметру бревна), то получится балка очень маленькой высоты и прочность ее будет мала (рис. 29, а). Мала будет прочность балки, если сделать ее слишком узкой (рис. 29, б). Чтобы найти, при каком соотношении длины и ширины прочность будет наибольшей, выразим прочность балки как функцию от ее ширины х. Из треугольника А B С, изображенного на рис. 28, видно, что высота балки, имеющей ширину х, равна √‾( 4 R² - х²). Поэтому прочность такой балки равна:
kx (4 R² - x²)=4 R² kx - kx³.
График функции у=4 R² kx-kx³ имеет вид, указанный на рис. 30, а ее производная равна 4R² k- 3 kx² и обращается в нуль при
x1,2 +(2 R √‾3)/3.
Поскольку ширина балки должна быть положительной, получаем, что самая прочная
балка будет, если ширина ее а=(2 R √‾ 3 )/ 3 ; высота
О
балки определится по формуле:
Отношение h/a равно √‾2 ≈ 7/5. Именно такое
отношение высоты балки к ширине и предписано правилами производства строительных работ.
Между дифференцированием и интегрированием имеется глубокая связь: формула (3) показывает, что путь находится по мгновенной скорости с помощью интегрирования, а формула (9) утверждает, что скорость находится по пути с помощью дифференцирования. Это наводит на мысль, что действия дифференцирования и интегрирования связаны друг с другом примерно так же, как действия сложения и вычитания, умножения и деления, возведения в степень и извлечения корня, т. е. что эти операции взаимно обратны.
Например, пользуясь тем, что v(t)=s'(t), можно записать формулу (3) в виде:
367
Здесь s - путь, пройденный телом начиная с момента t= 0.
Но может случиться и так, что пройденный путь отсчитывается не с момента t= 0, a с какого-то более раннего момента (например, не с момента начала путешествия, а с момента выпуска автомобиля с завода). Тогда путь s придется записать в виде разности s(T)- s(0) пути, пройденного к моменту t = T, и пути, пройденного к моменту t =0. Равенство (3) примет тогда такой вид:
Таким же образом для любых двух моментов времени t=a и t=b справедливо равенство:
Вообще, для любой функции F(x) имеет место равенство:
Эта формула называется формулой Ньютона - Лейбница - в честь знаменитых математиков И. Ньютона и Г. Лейбница, почти одновременно установивших ее в конце XVII в. (примерно через 70 лет после выхода в свет книги И. Кеплера «Новая стереометрия винных бочек»). Следует сказать, что в геометрической форме эту формулу высказал учитель Ньютона И. Барроу в 1670 г. Он указал, что вычисление площадей - действие, обратное проведению касательных.
Значение формулы Ньютона - Лейбница состоит в следующем: если мы знаем какую-нибудь функцию F(x), производная которой равна f(x), т. е. F' (х) = f (х), то легко вычислить интеграл
значений функций F(x) в точках b и а. Каждую функцию F(x), для которой F' (х) = f (х), называют первообразной для функции f(x). Значит, если функция F(x) - первообразная для функции f(x), то f(x) - производная для функции F(x).
Таким образом, вычисление интегралов сводится в основном к нахождению первообразных. А нахождение первообразных есть задача, обратная дифференцированию. Поэтому, чем
большее число функций мы будем уметь дифференцировать, тем больше первообразных будем знать и тем больше интегралов сможем найти. Пока что мы умеем дифференцировать только многочлены. Этого уже достаточно, чтобы интегрировать любые многочлены (не прибегая к примененным выше геометрическим приемам).
Но во многих задачах встречаются функции, отличные от многочленов. Мы научимся сейчас дифференцировать показательную и тригонометрические функции.
Производные от тригонометрических функций проще всего вычислить, исходя из физических соображений. Рассмотрим точку А, движущуюся по окружности радиуса R со скоростью w R. Будем считать, что при t =0 точка А находилась в положении А0 (рис. 31).
Через t сек. точка пройдет путь длиной w Rt и окажется в положении А. Дуга А0 А имеет длину w Rt, т. е. содержит w t радиан, значит, и угол АОА0 равен w t радиан. Поэтому координаты точки А равны х =Rcos w t и y=Rsin w t (это легко выводится из треугольника АВО). Иными словами, проекция В точки А на ось Ох движется по закону x = Rcos w t, а проекция С этой же точки на ось Оу движется по закону у= R sin w t. Найдем скорости этих колебаний.
Для этого разложим скорость движения точки А на две составляющие: горизонтальную и вер-
368
тикальную. Вектор скорости точки А (имеющий длину сой) направлен по касательной к окружности, проведенной в точке А, и потому образует с осью Ох угол w t+ p /2, а с осью Оу - угол
и
w t (рис. 32). Следовательно, его проекция на ось
Ох (т. е. скорость движения точки В) равна: vx = w R cos ( w t+ p /2) =- w R sin w t,
а его проекция на ось Оу (т. е. скорость движения точки С) равна:
vy = w R cos w t .
Мы доказали, что скорость колебания, происходящего по закону х= R cos w t, равна: vx =- w R sin w t. Так как скорость является производной от пути по времени, это означает, что
(R cos w t )'=- w R sin w t,
или при R =1
(cos w t)' =- w sin w t. (13)
Точно так же доказывается (из рассмотрения движения точки С), что
(sin w t)' = w cos w t. (14)
В частности, при w =1 мы получаем, что (cos t)'=- sin t; (sint)'= cos t.
Теперь продифференцируем показательную функцию у=ех . Мы уже знаем (см. статью «Функции в природе и технике»), что касательная к кривой у=ех, проведенная в точке пересечения ее с осью ординат, наклонена к осям под углом в 45°. Вспоминая геометрический смысл производной (см. стр. 364), мы можем сказать, что производная функции у=ех в точке х=0 равна tg45°, т. е. 1.
Итак, ( еx)'|приx=0 =1.
Чтобы сосчитать производную от функции у=ех в какой-либо точке х0, сдвинем график этой функции на отрезок х0. После сдвига в точке х ордината станет равной не ех, а ех-х0, т. е. сдвинутая кривая является графиком функции у=ех-х0 (рис. 33). При сдвиге графика касательная, проведенная к кривой у=ех в точке х =0, перейдет в касательную, проведенную к сдвинутой кривой (т.е. кривой у=ех- x 0) в точке х=х0 (рис. 34).
Таким образом, касательная к кривой у=ех-х0 в точке х0 наклонена к оси х под углом 45°, т. е.
( е x - x0)' |приx=x0 =1.
Теперь легко найти производную функции у=ех в точке х=х0. В самом деле, так как постоянный множитель ех0 можно вынести за знак производной, получим:
( ex)' |при х=х0 =( e к ex-x0)' |при х=х0 = еx0 (еx-x0)' |приx=x0 =еx0 ·1 = ex0 .
369
Этим доказано, что производная от функции ех в точке х=х0 равна ех0 . Так как х0 - произвольная точка, то мы можем просто написать:
(ех)'=ех .
Лишь немногим более сложные рассуждения показывают, что
(еC х)'= СеСх . (15)
Многие физические законы связывают между собой некоторую величину и скорость ее изменения. Рассмотрим, например, радиоактивный распад. Скорость распада тем больше, чем больше взято радиоактивного вещества. Это и понятно: если, скажем, в каждом грамме взятого радиоактивного вещества за 1 сек. распадается 0,0001 г, то в двух граммах этого вещества за 1 сек. распадается 0,0002 г, в семи граммах распадается за 1 сек. 0,0007 г и т. д. Иначе говоря, скорость распада (мы ее обозначали выше буквой и; см. формулу (10) прямо пропорциональна массе т имеющегося радиоактивного вещества:
и=- km. (16)
Здесь k - положительный коэффициент пропорциональности, а знак «-» поставлен потому, что вещество распадается и его становится меньше, т. е. скорость распада отрицательная. (Этот закон, связывающий массу радиоактивного вещества и скорость распада, справедлив лишь в случае, если количество радиоактивного вещества не слишком велико и не происходит цепной реакции.)
На первый взгляд кажется, что из уравнения (16) ничего нельзя определить: ведь это одно уравнение с двумя неизвестными u и m (коэффициент пропорциональности k для каждого вида радиоактивного вещества определяется из опыта), а для нахождения двух неизвестных надо иметь два уравнения. Однако второе уравнение легко найти: ведь и - это скорость изменения массы т, а потому и u = m '. Поэтому мы можем переписать закон радиоактивного распада (т. е. формулу (16) в виде:
m ' =- km. (17)
Мы получили одно уравнение для определения одного неизвестного т. Только это уравнение не такое, какие изучаются в школе: оно связывает величину т и ее скорость изменения (производную). Уравнения, связывающие величины и их производные, называются дифференциальными уравнениями. Легко проверить, что функция т = Се- kt, где С - любое число, является решением дифференциального уравнения (17) (т. е. если подставить в это уравнение вместо т эту функцию, то оно обратится в тождество). В самом деле:
m '=(Се- kt)' =- Cke-kt =- km.
Можно показать, что других функций (кроме m(t)=Ce-kt), удовлетворяющих уравнение (17), не существует, т. е. что всякое решение уравнения (17) имеет вид: m(t)=Ce-kt . Это и есть закон уменьшения массы радиоактивного вещества с течением времени.
У нас остался невыясненным один вопрос: чему равна постоянная C? На этот вопрос нетрудно ответить. Из формулы т (t) = Се- kt находим (полагая t =0), что масса радиоактивного вещества в начальный момент времени t =0 была равна Се 0 = С. Таким образом, С - это масса радиоактивного вещества в начальный момент времени; ее принято обозначать через m0. Поэтому, заменяя С на m0, получаем окончательный вид закона радиоактивного распада:
т (t)=m0 е- kt . (18)
Найдем теперь, через сколько лет количество радиоактивного вещества уменьшится вдвое. Для этого нужно определить число
Т0 из уравнения e-kT0 =1/2. После логарифмирования (по основанию е) находим, что Т0 =1/ kln2 ≈ 0,69/k (через ln x мы обозначаем
логарифм числа х по основанию е). Этот промежуток времени Т0 называют периодом полураспада данного радиоактивного вещества. Он не зависит от того, сколько было взято радиоактивного вещества, а зависит только от k, т. е. от того, какое взято вещество. Например, период полураспада радия равен 1590 годам, урана-238 - 4,5 млрд. лет, тория С всего 0,0000003 сек. С помощью числа Т0 закон радиоактивного распада можно записать так:
m(t)=m0 (e-kT0)t/T0 =m0 (1/2)t/T0 .
В этой форме его обычно и используют в физике.
370
Существует огромное количество процессов в природе, которые описываются такими же дифференциальными уравнениями, как уравнение (17) для радиоактивного распада. Общим для всех этих процессов является то, что скорость изменения рассматриваемой величины у прямо пропорциональна значению этой величины в данный момент времени, т. е.
y '=су. (19)
Коэффициент пропорциональности с положителен или отрицателен в зависимости от того, увеличиваются или уменьшаются с течением времени значения величины у. Дифференциальное уравнение (19) имеет точно такой же вид, как и уравнение радиоактивного распада (только коэффициент пропорциональности здесь обозначается через с, а не через - k). Так как одинаковые уравнения имеют одинаковые решения, то для всех таких процессов значения у0 в любой момент времени t выражаются формулой:
y(t)=y0 ect,
где у0 - значение величины у при t = 0. Теперь становится понятным, почему в природе и технике встречается так много величин, изменяющихся по показательному закону (ток самоиндукции, протекающий в катушке после выключения постоянного напряжения; изменение давления с высотой подъема и т. д.; см. статью «Функции в природе и технике»). Все эти величины удовлетворяют дифференциальным уравнениям вида (19).
Леверье и Адамс открывают новую планету
По второму закону Ньютона сила равна произведению массы на ускорение:
F = ma .
Но ускорение тела, движущегося прямолинейно, представляет собой скорость изменения скорости, т. е. является производной от скорости a=v'. Сама же скорость является производной от пройденного пути: v=s'. Таким образом, чтобы найти ускорение движущегося тела, надо два раза продифференцировать функцию s(t). Поэтому ускорение называют второй производной от пути по времени. Обозначают это так: a(t) = s"(t). Пользуясь этим обозначением, мы можем за-
писать второй закон Ньютона в следующем виде:
F=ms".
Сила F зависит от многих обстоятельств: от времени, от скорости движения, от того, в какой точке пространства находится движущееся тело. Например, на парашютиста, спускающегося с раскрытым парашютом, действуют сила тяжести mg и сила сопротивления воздуха, которую можно считать пропорциональной скорости падения, т. е. равной - kv. Таким образом, общая сила, действующая на парашютиста, равна:
F=mg-kv = mg-ks'.
Следовательно, движение парашютиста описывается дифференциальным уравнением ms"=mg-ks'.
Иной вид имеет уравнение движения ракеты, вертикально поднимающейся по инерции после полного сгорания горючего. Сила притяжения ракеты к Земле обратно пропорциональна квадрату расстояния ракеты от центра Земли, т. е.
F=-k/s²
(мы считаем, что ракета вышла из земной атмосферы и потому на нее не действует сила сопротивления воздуха).
Таким образом, указанное движение ракеты описывается дифференциальным уравнением
ms''=-k/s²,
где m - масса ракеты. (Этим уравнением описывается также вертикальное падение метеорита на Землю до вхождения его в атмосферу.)
Вообще, второй закон Ньютона позволяет описывать самые разнообразные движения тел с помощью дифференциальных уравнений. Можно написать дифференциальные уравнения для движения поршня паровой машины, корабля в море, планеты вокруг Солнца, искусственного спутника вокруг Земли.
Решая дифференциальные уравнения движения планет и их спутников (эти уравнения весьма сложны, так как планеты притягиваются не только к Солнцу, но и друг к другу), ученые предсказывают их будущее движение, узнают моменты солнечных и лунных затмений. Когда однажды оказалось, что планета Уран отклоняется от заранее вычисленной орбиты, ученые нисколько не усомнились в «правильности» математики. В середине XIX в.
371
французский астроном У. Леверье и английский астроном Дж. Адамс одновременно и независимо один от другого сделали смелое предположение, что отклонение Урана вызывается притяжением новой, до тех пор неизвестной планеты. С помощью дифференциальных уравнений они высчитали положение этой новой планеты и указали, где нужно ее искать на небе. Точно в указанном месте эта планета (ее назвали Нептуном) была затем обнаружена.
Во многих случаях тела совершают колебания около положения равновесия под действием силы, величина которой пропорциональна отклонению тела от положения равновесия и которая стремится возвратить это тело в положение равновесия. Например, это имеет место для груза, подвешенного на пружине. Иначе говоря, сила, действующая на тело, выражается формулой:
F=-ks,
где s - отклонение тела от положения равновесия, а k - жесткость пружины. Поэтому (в силу второго закона Ньютона) дифференциальное уравнение движения тела имеет такой вид:
ms" =- ks.
Обозначив положительное число k/m через w²,
мы сможем записать это уравнение в виде:
s'' =- w² s.
Это уравнение называется уравнением гармонических колебаний, так как функция
s=C1 cos w t+ С2 sin w t (20)
при любых С1 и C2 является решением этого уравнения.
В самом деле, по формулам (13) и (14) скорость тела, движущегося по закону (20), равна:
v = s'=- C1 w sin w t + С2 w cos w t. Продифференцировав еще раз, найдем ускорение:
s" =- C1 w² cos w t- С2 w² sin w t =- w² ( C1 cos w t + С2 sin w t). Но выражение, стоящее в скобках, равно s. Таким образом, взятая функция s действительно удовлетворяет уравнению s"=- w² s. Можно доказать, что всякое решение этого уравнения имеет такой вид.
Итак, сила, пропорциональная отклонению тела от положения равновесия и стремящаяся вернуть его в это положение, вызывает гармонические колебания частоты w, где w² = k/m
( m - масса тела, k - коэффициент пропорциональности).
Магический шестиугольник
В этом шестиугольнике образовалось 19 узловых точек. Вот и расставьте в этих точках 19 натуральных чисел от 1 до 19 так, чтобы вдоль каждой стороны и вдоль каждого внутреннего прямолинейного отрезка сумма чисел равнялась 38 (должно получиться 15 одинаковых сумм по 38). Ответ на стр. 373.
Игра с кубами чисел
У каждого участника игры должна быть таблица кубов. Назначаем какое-нибудь целое число и ставим задачу: представить это число как алгебраическую сумму пяти кубов.
Пусть назначено, например, число 1. Рассматриваем таблицу кубов и подбираем:
1=4³ -3³ -3³ -2³ -1³ или 1=6³ -5³ -4³ -3³ +1³
Цель игры: за отведенный промежуток времени подобрать как можно больше решений задачи.
У вас, очевидно, возникнет такой вопрос: разве любое целое число может быть представлено в виде алгебраической суммы пяти кубов натуральных чисел, да еще несколькими способами?
Да, любое и даже бесконечным числом способов. Это доказал польский математик В. Серпинский.
372
Для колебаний электрической цепи можно также записать аналогичный закон, только надо заменить массу тела самоиндукцией катушки, путь, пройденный телом,- напряжением на конденсаторе, а скорость тела - током и т. д. Поскольку законы, управляющие этими явлениями, совершенно аналогичны, то и колебания, возникающие в обоих случаях, записываются одними и теми же формулами. А затухающие колебания возникают, если, кроме силы, стремящейся вернуть тело в положение равновесия, действует еще сопротивление среды, пропорциональное скорости движения тела (или сопротивление электрической цепи).
Тот факт, что самые различные явления описываются одинаковыми дифференциальными уравнениями, часто используется на практике.
Он позволяет изучать одни явления, наблюдая другие, если только оба явления описываются одинаковыми уравнениями. Пусть, например, надо выяснить, как будет двигаться под землей нефть в районе буровых скважин.
Наблюдать движение нефти под землей было бы очень затруднительно. Но движения жидкости описываются теми же самыми дифференциальными уравнениями, что и движения электричества. Поэтому собирают электрическую цепь, в которой движения электричества происходят так же, как изучаемые движения нефти.
Измеряя напряжение и ток в разных точках собранной цепи, можно узнать, где выгоднее всего поставить буровую вышку, куда надо накачивать воду, чтобы усилить выход нефти, и т. д.
Такое изучение одних явлений при помощи других, описываемых теми же самыми уравнениями, называется моделированием явлений. К нему часто прибегают в самых различных вопросах техники.
Ответы и решения
Ответ к стр. 326. 2165904378 и 2934815607.
Ответ к стр. 328. 1 000 000 000=109 =(2·5)9 =29 ·59 =512·1953125. 1 000 000 000 000 000 000=1018 =218 ·518 =262 144·3 814 697 265 625.
Ответ к стр. 329.
1) 849+753 =1602;
2) 1089-432=657;
3) 7039·4 = 28156;
4) 27504:9168=3;
5) 50/(4· 7-8)=(9+1)/³ √‾26 .
В каждом равенстве, как видите, присутствуют все 10 цифр. Возможны и другие решения.
Доказательство к стр. 353.
Пусть начальное число x ; разность 1- х;
число, обратное разности:1/(1- x) .
Повторяем цикл:
1- 1/(1-x)=-x/(1-x);
число, обратное разности:
-(1- х)/ x. Повторяем еще раз:
1-(-(1- x)/x)=1/x; число, обратное этой разности: x .
Ответ к стр. 353.
a =12, b =5, c =13. Решение к стр. 353. (121)B = 1 ·В² + 2 ·В+ 1·В0 =В² +2 B +1=(В+1)² .
Ответ к стр. 372.
Обычно арифметику определяют как науку о числах. Числа в простейшем смысле слова, т. е. так называемые натуральные числа: 1, 2, 3, 4, 5, ..., отвечают на вопрос «сколько?». Сколько учеников в классе? Сколько книг на столе? Сколько гусей на пруду?
Но каждый раз, когда мы спрашиваем: «Сколько предметов?» - мы должны иметь эти предметы, их совокупность. Вот мы и говорим о совокупности всех учеников, образующих данный класс, о совокупности книг, лежащих на столе, о совокупности гусей, плавающих на пруду. Каждое натуральное число есть число предметов (одушевленных или неодушевленных), образующих некоторую совокупность. Иногда эти предметы легко сосчитать, например когда идет речь о числе книг, лежащих на столе, или о числе учеников, сидящих в классе.
Но значительно труднее ответить на вопрос, сколько в данный момент плавает китов в миро-
374
вом океане или даже сколько ежиков живет в подмосковных лесах. И уж совсем трудно точно сказать, сколько молекул в стакане воды или звезд в нашей Галактике. Однако во всех этих случаях мы уверены, что число это конечное, хотя, может быть, и очень большое и недоступное для точного вычисления при данном состоянии наших научных познаний.
В математике рассматриваются не только конечные, но и бесконечные совокупности. Простейшим примером такой совокупности является совокупность, или, как принято говорить, множество, всех натуральных чисел: 1, 2, 3, 4, 5, ... .
Мы уже сказали, что каждое натуральное число есть число предметов, образующих ту или иную совокупность, то или иное множество. Но множество всех натуральных чисел уже не есть конечное множество. На вопрос: «Сколько всего натуральных чисел?» - приходится ответить, что их бесконечно много. Какое бы большое число натуральных чисел мы ни задумали, всегда есть такие натуральные числа, которые не вошли в число задуманных.
Рис.1.
В математике мы постоянно сталкиваемся с примерами бесконечных множеств. Возьмем, например, равносторонний треугольник T1 впишем в него равносторонний треугольник T2. Вершины треугольника T2 суть середины сторон треугольника T1. Таким же образом впишем в T2 равносторонний треугольник T3, в T3 впишем T4 и т. д. (рис.1). Это построение приводит к бесконечному множеству равносторонних треугольников:
T1, T2, T3, T4, T5,... Tn,... . (1)
Тем более бесконечным является множество всех вообще равносторонних треугольников, лежащих в данной плоскости.
Последняя фраза несколько двусмысленна: слово «более» может быть воспринято в ней как составная часть выражения «тем более», употребленного в смысле «и подавно». Раз есть уже бесконечное множество равносторонних треугольников, получающихся при некотором определенном построении, то и подавно множество всех равносторонних треугольников бесконечно. Но слово «более» может быть понято и как сравнительная степень прилагательного, и тогда высказанное выше суждение означает, что множество всех равносторонних треугольников, лежащих в данной плоскости, в каком-то смысле является «более бесконечным», чем бесконечное множестве» построенных нами треугольников
T1, T2, T3…, Tn,…
Как видите, мы затронули интересный вопрос, долгое время отпугивавший ученых: своей (впрочем, лишь кажущейся) парадоксальностью: существуют ли, если можно так выразиться, различные «степени» бесконечности? Возможна ли количественная оценка бесконечных множеств, позволяющая утверждать, что одно из двух бесконечных множеств является «более бесконечным», чем другое? Или же утверждение, что данное множество является бесконечным, окончательно в том смысле, что не дает возможности дальнейших различений или градаций количественного характера.
Первым, кто пытался ответить на этот вопрос, был знаменитый чешский математик и философ Б. Больцано (1-я половина XIX в.), но он не сумел полностью преодолеть все трудности, которые при этом возникли. Постараемся разобраться, в чем эти трудности и каково решение поставленного вопроса.
Предположим, что мы имеем два конечных множества, например корзину яблок и корзину груш. Желая установить, чего у нас больше - яблок или груш, мы можем (и это будет самое простое решение вопроса) сосчитать число плодов в каждой корзине. Получим два числа, - сравнение их и даст ответ на наш вопрос.
Но если мы имеем два бесконечных множества, то определить аналогичным образом, какое из них является «более бесконечным», а какое - «менее», нельзя по той простой при-
375
Бернард Больцано.
чине, что бесконечное множество нельзя «сосчитать». Во всяком случае, мы не знаем, как это сделать. Поэтому постараемся ответить на вопрос, чего у нас больше - яблок или груш, не сосчитывая их, т. е. не пользуясь понятием числа. Вот какой представляется для этого путь.
Разложим наши яблоки, хотя бы на столе, и попробуем положить против каждого яблока по груше. Возможны три случая (рис.2).
Первый случай: против каждого яблока действительно окажется груша, и при этом не только все яблоки, но и все груши окажутся разложенными. В этом случае, очевидно, у нас столько же яблок, сколько и груш.
Второй случай: против каждого яблока окажется по груше, но при этом еще останется несколько груш в корзине - в этом случае у нас больше груш, чем яблок.
Наконец, возможен последний, третий случай: стараясь разложить все груши так, чтобы против каждого яблока лежала груша, мы не достигнем цели - нам не хватит груш. Тогда, очевидно, груш меньше, чем яблок.
Как видите, мы смогли произвести количественную оценку двух множеств - корзины яблок и корзины груш, не сосчитывая точно, сколько имеется тех и других плодов, но установив, каких плодов больше, или убедившись, что их имеется одинаковое количество. Эту оценку мы произвели, установив, как говорят, взаимно-однозначное соответствие между одним множеством и другим или частью другого. Для лучшего уяснения, что такое взаимно-однозначное соответствие между двумя множествами, приведем еще несколько примеров.
Дается концерт. Чтобы на него пойти, надо купить билет. Перед нами два множества: множество людей, которые хотят пойти на этот концерт,- обозначим его через A и множество билетов - обозначим его через B. Возможны разные случаи. Первый (не очень вероятный, но математически самый простой): все желающие пойти на концерт приобрели билеты, и все билеты при этом оказались проданными. Тогда каждому элементу множества A (т. е. каждому человеку, желающему пойти на концерт) соответствует определенный элемент множества B (купленный этим человеком билет). При этом каждый элемент множества B поставлен в соответствие одному-единственному элементу множества A (человеку, купившему этот билет). Установлено взаимно-однозначное соответствие между множеством A и множеством B, или установлено взаимно-однозначное отображение одного из этих множеств на другое.
Однако может случиться, что каждый человек, желавший пойти на концерт, купил себе билет, но в кассе остались еще не распроданные билеты. Опять получается взаимно-однозначное отображение множества A, но уже не на все множество B, а только на некоторую его часть - на ту часть, или, как говорят, на то подмножество, множества B, которое состоит из всех проданных билетов. Может, наконец, случиться, что все билеты проданы, но не все желающие пойти на концерт смогли купить билеты. Тогда обозначим через A′ множество тех людей, которые не только хотели пойти на концерт, но и получили на него билет. Множество A′ оказалось взаимно-однозначно отображенным на множество B.
В математике можно найти многочисленные примеры взаимно-однозначных соответствий. Например, каждой вершине треугольника или
376
тетраэдра соответствует противоположная этой вершине сторона или грань. Таким образом, установлено взаимно-однозначное соответствие между множеством всех вершин треугольника (тетраэдра) и множеством всех его сторон (граней). Множество всех сторон правильного многоугольника находится во взаимно-однозначном соответствии с множеством всех перпендикуляров, которые опущены на эти стороны из центра правильного многоугольника. Множество всех боковых граней пирамиды находится во взаимно-однозначном соответствии с множеством апофем этой пирамиды и т. д.
Особенно существенным является тот факт, что взаимно-однозначное соответствие возможно и между некоторыми бесконечными множествами. Приведем примеры. Обозначим через A множество всех точек данной окружности, а через В - множество всех прямых, являющихся касательными к этой окружности (рис.3, 1). Между множествами A и В установится взаимно-однозначное соответствие, если мы каждой точке окружности поставим в соответствие касательную в этой точке. Таким образом, каждому элементу множества A соответствует единственный элемент множества В, и каждый элемент множества В (т. е. каждая касательная) при этом поставлен в соответствие единственному элементу множества A - точке прикосновения данной касательной.
Второй пример. Возьмем две пересекающиеся прямые a1 и b1 (рис.3, II). Обозначим через A множество всех точек прямой a1, а через В - множество, состоящее из прямой b1 и из всех прямых, ей параллельных. Каждому элементу b множества В (т. е. каждой прямой b, параллельной прямой b1 или совпадающей с ней) соответствует единственный элемент множества A - единственная точка прямой a1, в которой ее пересекает прямая b .
В качестве третьего примера возьмем уже рассмотренное нами множество равносторонних треугольников
T1, T2,...Tn,... ,
каждый из которых, кроме первого, вписан в предыдущий (рис.3, III). Множество всех этих треугольников обозначим через X. Каждый треугольник получил определенное натуральное число n в качестве своего номера.
Номером треугольника Tn является натуральное число n. Этим, очевидно, установлено взаимно-однозначное соответствие между множеством X наших треугольников и множеством всех натуральных чисел.
Вообще, если все элементы какого-нибудь множества X удается занумеровать посредством натуральных чисел так, что каждое натуральное число придано в качестве номера лишь одному элементу множества X, то такой нумерацией устанавливается взаимно-однозначное соответствие между данным множеством X и множеством всех натуральных чисел. И обратно, всякое взаимно-однозначное соответствие между каким-нибудь множеством X и множеством всех натуральных чисел можно рассматривать как нумерацию (сосчитывание) элементов множества X посредством натуральных чисел,- мы просто приписываем каждому элементу множества X в качестве номера соответствующее ему натуральное число.
Мы здесь коснулись очень важного понятия. Ведь установление взаимно-однозначного соответствия между некоторым множеством X и множеством всех натуральных чисел есть прямое перенесение в область бесконечных множеств пересчитывания какого-либо конечного множества (например, корзины яблок или стада гусей) с помощью натуральных чисел. Только в случае конечных множеств мы для сосчитывания его элементов нуждаемся лишь в конечном числе чисел (мы считаем: раз, два, три и т. д.- до того числа, которое показывает, сколько у нас яблок в корзине или гусей в стаде). В примере множества треугольников
T1, T2, T3, ..., Tn,... (1)
или вообще любого множества X, которое может быть приведено во взаимно-однозначное соответствие с множеством всех натуральных чисел, мы вынуждены в качестве номеров пользоваться всеми натуральными числами.
377
Но теперь возникает самый главный, основной для всей теории множеств вопрос. Всегда ли можно занумеровать элементы бесконечного множества натуральными числами так, чтобы каждый элемент данного множества получил определенный номер? Другими словами, можно ли установить взаимно-однозначное соответствие между произвольным бесконечным множеством и множеством всех натуральных чисел?
Оказывается, ответ на этот вопрос отрицательный, и мы постараемся убедиться в этом. Но сначала несколько подготовимся. Прежде всего установим название для тех множеств, которые могут быть поставлены во взаимно-однозначное соответствие с множеством всех натуральных чисел. Эти множества называются счетными. Это название естественно: счетное множество - это такое множество, которое может быть сосчитано посредством натуральных чисел. Наша задача - показать, что существуют несчетные множества, т. е. такие, которые не могут быть поставлены во взаимно-однозначное соответствие с множеством всех натуральных чисел.
В поисках несчетного множества обратимся к множеству всех рациональных чисел (читатель, конечно, помнит, что рациональными называются все целые и все дробные числа). Посмотрим, можно ли занумеровать все рациональные числа с помощью натуральных. Для простоты рассмотрим сначала все положительные рациональные числа и попробуем их как-нибудь занумеровать. Сразу же сталкиваемся с трудностью: среди положительных рациональных чисел заведомо нет наименьшего числа, каким является единица среди натуральных чисел: ведь каково бы ни было положительное рациональное число r, число 1⁄2 r также является положительным рациональным числом, и оно меньше, чем r. Предположим, мы обойдем эту трудность, начав счет с какого-нибудь рационального числа r 1, которое согласимся считать первым. Но тогда на следующем этапе возникает такая трудность: какое рациональное число считать вторым, т. е. непосредственно следующим в порядке нашего счета за числом r 1? Дело в том, что, какое бы рациональное число r 2 > r1 мы ни взяли, имеются рациональные числа большие, чем r 1, и меньшие, чем r 2, и таких бесконечное множество, например числа:
r3 = 1/2 (r1 + r2), r4 = 1/2 (r1 +r3),...
Таким образом, среди всех рациональных чисел, больших, чем выбранное нами число r1, нет наименьшего. Какое же объявить первым из следующих за r1? Но возникшая трудность - кажущаяся. Она показывает только, что невозможно занумеровать рациональные числа с помощью натуральных чисел таким образом, чтобы при этой нумерации возрастающим номерам соответствовали возрастающие числа. Придется попытаться занумеровать рациональные числа как-нибудь иначе, не стремясь к тому, чтобы число r2, первое после r, в порядке нашего счета, было и первым по величине, т. е. наименьшим из всех следующих за r1. А тогда нужная нам нумерация находится очень легко.
В самом деле, каждое положительное рациональное число однозначно записывается в виде несократимой дроби p⁄q (целое число n будем при этом записывать в виде дроби n⁄1 и также считать ее несократимой). Назовем высотой дроби - натуральное число q+р.
Под высотой рационального числа будем понимать высоту той единственной несократимой дроби, которая является записью данного рационального числа.
Посмотрим, сколько приходится рациональных чисел на каждую данную высоту. Высоту 1 не имеет ни одно положительное рациональное число (потому что, записывая рациональное число в виде несократимой дроби p⁄q, видим, что ее высота равна натуральному числу р + q, а так как p ≥ 1, q ≥ 1, то р+q ≥ 2). Высоту 2 имеет, очевидно, единственное рациональное число 1⁄1 = 1.
Высоту 3 имеют дроби 1⁄2 и 2⁄1, т. е. рациональные числа 1⁄2 и 2.
Высоту 4 имеют дроби 1⁄3, 2⁄2, 3⁄1. Среди них оставляем лишь несократимые 1⁄3 и 3⁄1. Итак, высоту 4 имеют рациональные числа 1⁄3 и 3.
Высоту 5 имеют дроби 1⁄4, 2⁄3, 3⁄2, 4⁄1, среди
378
которых нет сократимых, так что на высоту 5 приходится 4 числа.
Высоту 6 имеют дроби 1⁄5, 2⁄4, 3⁄3, 4⁄2, 5⁄1, среди которых несократимыми являются лишь первая и последняя; следовательно, высоту 6 имеют числа - 1⁄5 и 5.
Продолжая рассуждать таким образом дальше, мы прежде всего убеждаемся в том, что, каково бы ни было натуральное число h >1, есть лишь конечное число рациональных чисел с этой высотой.
В самом деле, дроби с высотой h - это, очевидно,
1⁄(h−1), 2⁄(h−2), ... (h−1)⁄1.
Их конечное число: h−1. Среди этих дробей некоторые могут оказаться сократимыми, а остальные дадут рациональные числа с высотой h.
Теперь уже очень легко занумеровать все положительные рациональные числа: мы начинаем с наименьшей высоты 2 и идем дальше, все время увеличивая на единицу высоту и сосчитывая то (всегда конечное) число рациональных чисел, которое приходится на данную высоту. Таким образом, число 1 = r1 получает номер 1. Далее идут два числа: r 2 =1⁄2 и r 3 = 2 высоты 3,
потом два числа: r 4 =1⁄3 и r 5 = 3 высоты 4,
потом четыре числа: r 6 = 1⁄4, r 7 = 2⁄3, r 8 = 3⁄2, r 9 = 4 высоты 5,
два числа: r 10 = 1⁄5, r 11 = 5 высоты 6 и т. д. Получаем таблицу (через nh обозначено число рациональных чисел высоты h):
Так как каждое рациональное число имеет своей высотой некоторое натуральное число h, оно найдет свое место в строке, соответствующей этой высоте, и получит определенный номер, не больший, чем число n2 + n3 +...+ nh−1 + nh.
Итак, множество всех положительных рациональных чисел есть счетное множество.
И тем не менее несчетные множества существуют. Оказывается, множество всех действительных чисел - несчетно. Этот замечательный факт, как и теорема о счетности множества всех рациональных чисел, впервые в 1874 г. был доказан знаменитым немецким математиком Г. Кантором, основателем современной теории множеств.
Георг Кантор.
Воспроизводим доказательство Кантора. Доказываем, что несчетным является уже множество всех действительных чисел интервала 1 (0; 1).
Каждое такое действительное число может быть записано в виде бесконечной десятичной дроби с целой частью нуль. При этом каждому действительному числу соответствует лишь одна такая запись, за исключением действительных чисел, выражаемых конечными десятичными дробями: каждое такое число, например 0,2476622021711, может быть записано двумя способами в виде бесконечной десятичной дроби:
0,2476622021711000000000... и
0,2476622021710999999999...
Одна из этих записей начиная с некоторого момента содержит одни лишь нули, а другая - одни девятки. Если мы согласимся не употреб-
1 Под интервалом (a; b) числовой прямой понимается множество всех действительных чисел x, удовлетворяющих неравенству a < x < b.
379
лять записей, в которых, начиная с какого-нибудь места, идут одни девятки, то каждое действительное число будет иметь лишь единственную запись в виде бесконечной десятичной дроби. Докажем теперь теорему о несчетности множества действительных чисел от противного: предположим, что множество действительных чисел [мы говорим все время о числах X интервала (0 ; 1)] счетно, т.е. может быть занумеровано посредством натуральных чисел. Тогда вся совокупность действительных чисел интервала (0 ; 1) может быть записана в виде последовательности: х1, х2 ,...
Запишем разложение числа xn в бесконечную десятичную дробь в виде:
xn = 0, а(n)1 а(n)2 а(n)3 а(n)4 ... а(n)n,
где а(n)1, а(n)2, а(n)3, ... суть последовательные десятичные знаки числа xn, причем, согласно заключенному нами условию, не может случиться, что все десятичные знаки начиная с некоторого суть девятки.
Итак, все действительные числа х [интервала (0; 1)] предполагаются записанными в виде:
Приведем наше предположение к противоречию, найдя действительное число с, заключенное между 0 и 1 и заведомо не входящее в табл.I. Для этого рассмотрим цифры, стоящие по диагонали в табл.I, а именно:
а(1)1,а(2)2,а(3)3,а(4)4,а(5)5,..., а(n)n,...,
и выберем для каждого n натуральное число bn, не превосходящее число 8 и отличное от числа a(n)n (например, при а(n)n < 8 полагаем bn =а(n)n + 1, а при a(n)n = 8 полагаем bn = 7). Рассмотрим бесконечную десятичную дробь
0, b1 b2 b3 b4 b5... bn....
Она не содержит ни одной девятки и выражает число c, заключенное между 0 и 1, заведомо отличное от всех чисел х1, x2, x3, ..., хn,... В самом деле, если бы было:
с = хn = 0, а(n)1 a(n) 2 ... а(n)n ...,
то на n-м месте в разложении числа c мы должны были бы иметь цифру а(n)n, тогда как действительно имеем bn ≠ a(n)n. Теорема доказана.
Нам нужно осмыслить полученный результат и подвести некоторые итоги всему до сих пор сказанному. Мы начали с понятия взаимно-однозначного соответствия между двумя
Начертите замкнутую кривую, пересекающую себя 10-12 раз. Но кривая может пересечь себя в каждой точке не больше одного раза. Все точки пересечения обозначьте различными буквами (в любом порядке). Теперь поставьте карандаш на любую не узловую точку и двигайтесь вдоль кривой, как бы повторил ее построение. Проходя узловую точку, называйте букву, которой точка обозначена.
Обойти надо всю кривую и вернуться в исходный пункт. На каком-нибудь этапе движения назовите две последовательно проходимые буквы, но не в порядке их следования, а наоборот. Например, если за буквой В следует буква F, вы произносите вслух не <В, F>, a <F, В>. Мне не сообщайте о такой перестановке последовательности двух букв, но запомните это место. Я его угадаю.
Фокус основан на теореме теории узлов. Угадывающему надо записывать называемые буквы на полоске бумаги поочередно сверху черты и снизу. Если перестановки букв не было, то каждая буква появится однажды сверху и однажды снизу черты. Если перестановка была, то одна буква появится дважды сверху и одна дважды снизу. Вот в этих буквах и была перепутана их последовательность! Пример. Мне называют буквы: С, С, Е, А, В, D, Е, A, D, В.
Я записываю:
Замечаю, что сверху черты два раза встречается Е, а снизу - два раза А. Значит, узлы Е и A были названы не в той последовательности, в которой они действительно располагались.
380
множествами, возможность которого (в случае конечных множеств) равносильна тому, что оба множества состоят из одного и того же числа элементов. Это обстоятельство указывает путь и к установлению количественного равенства, или количественной эквивалентности, между двумя бесконечными множествами. Мы скажем, что два (конечных или бесконечных) множества количественно эквивалентны, или имеют одну и ту же мощность, если между ними возможно установить взаимно-однозначное соответствие. Понятие «одинаковой мощности» означает для конечных множеств, что они состоят из одного и того же числа элементов.
Далее скажем, что множество A имеет большую мощность, чем множество B, если можно множество B отобразить взаимно-однозначно на часть множества A и в то же время нельзя отобразить множество A на часть множества B. Теперь можем сказать, что счетные множества - это множества, количественно эквивалентные множеству натуральных чисел. Но существуют множества и несчетные, например множество всех действительных чисел, интервала (0 ; 1) и любого другого интервала 1 .
Для того чтобы убедиться в том, что всякое несчетное множество имеет большую мощность, чем каждое счетное множество (все счетные множества имеют, очевидно, одну и ту же мощность), надо доказать следующие два предложения:
1. Всякое подмножество счетного множества или конечно, или счетно.
2. Всякое бесконечное (значит, в частности, всякое несчетное) множество содержит счетное.
Доказательство первого утверждения. Пусть X - счетное множество, Х0 - какое-нибудь подмножество (т. е. часть) множества X. Элементы множества X могут быть занумерованы посредством натуральных чисел, т. е. записаны в виде:
x1, x2, x3,..., x n .... (2)
Среди этих элементов содержатся и все элементы множества Х0. Пусть это будут - в порядке возрастания номеров в последовательности (2) - элементы:
xn1, xn2, xn3,... xnk,... (3)
Возможно одно из двух: или последовательность (3) обрывается на каком-то конечном шаге k, т. е. множество Х0 состоит из конечного числа элементов: xn1, xn2,... xnk, или же мы имеем бесконечную последовательность: xn1, xn2,... xnk, ..., которую можем переписать, полагая y1 = хn1, у2 = хn2,..., yk =xnk ,..., в виде:
y1, y2,... yk, ...,
непосредственно показывающем, что Х0 - счетное множество.
Доказательство второго утверждения. Пусть X - бесконечное множество. Выбираем в X какой-нибудь элемент x1.
Несомненно, в X имеются элементы, отличные от х1 (иначе X состояло бы из одного элемента и было бы конечным). Возьмем один из таких элементов и обозначим его через x2. Элементы х1 и х2 не исчерпывают множества X, поэтому существует элемент х3 множества X, отличный как от х1, так и от x2. И так далее. Продолжая этот процесс, получим счетное множество: x1, x2, x3,..., xn ,..., содержащееся в X.
Итак, на вопрос, поставленный в начале нашего изложения: существуют ли бесконечные множества разных «степеней бесконечности» (т. е. разных мощностей),- мы можем ответить утвердительно: существуют состоящие. из действительных чисел множества двух различных мощностей - множество всех действительных чисел какого-нибудь интервала, с одной стороны, и любое счетное множества действительных чисел (например, множество положительных рациональных чисел) - с другой. К этому выводу мы пришли, обосновывая количественную оценку бесконечных множеств, при помощи понятия взаимно-однозначного соответствия. Однако не следует думать, что взаимно-однозначное соответствие между бесконечными множествами во всем похоже на взаимно-однозначное соответствие между множествами конечными.
Очевидно, никакое конечное множество нельзя взаимно-однозначно отобразить на свою часть (часть никогда не равна целому). Уже простейшие примеры показывают, что это утверждение решительно перестает быть верным в области бесконечных множеств: мы видели, что всякое бесконечное подмножество счетного множества счетно, т. е. счетное множество может быть взаимно-однозначно отображено на всякую свою бесконечную часть. Например,
1 Всякий интервал числовой прямой может быть взаимно-однозначно отображен на интервал (0; 1) например, подобным растяжением или сжатием).
381
·подписывая под всеми натуральными числами подряд все четные:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10,...,
2, 4, 6, 8, 10, 12, 14, 16, 18, 20,...,
получим взаимно-однозначное соответствие между множеством всех натуральных чисел и его частью - множеством одних лишь четных чисел.
Другой пример: существует взаимно-однозначное отображение между множеством всех действительных чисел (между всей числовой прямой) и любым ее интервалом.
Для того чтобы получить такое соответствие, можно поступить так. Построим в плоскости окружность, касающуюся сверху оси абсцисс, и возьмем нижнюю полуокружность PQ этой окружности (рис.4). Концы Р и Q полуокружности к ней не причисляются. Установим взаимно-однозначное соответствие между всеми точками полуокружности PQ и всеми точками числовой прямой. Для этого сначала поставим в соответствие каждой точке x прямой ту точку h полуокружности, в которой ее пересекает луч, идущий из центра окружности в точку x .
Теперь спроектируем полуокружность PQ на интервал Р' Q' оси абсцисс и поставим в соответствие точке h полуокружности ее проекцию h' .
В результате каждой точке x прямой оказалась поставленной в соответствие точка h' интервала P'Q', и полученное соответствие есть взаимно-однозначное отображение всей числовой прямой на интервал P'Q'.
Можно доказать и другие, кажущиеся на первый взгляд парадоксальными, теоремы
«Совершенство» совершенных чисел не исчерпывается совпадением числа и суммы его делителей (см. стр. 325). Любители и профессионалы-математики со временем обнаружили еще несколько любопытных особенностей таких чисел, например:
а) каждое из известных совершенных чисел может быть представлено:
1) в виде произведения 2p-1 (2р-1), где p -простое число:
V1 = 6 = 2 (2² -1);
V2 = 28 = 2² (2³ -1);
V3 = 496 = 24 (25 -1);
V4 = 8128 = 26(27 -1);
V5 = 33550336 = 212 (213 -1);
2) в виде суммы последовательных степеней числа 2 от 2p-1 до 2² (p-1):
V1 = 6 = 2+2² ;
V2 = 28 = 2² +2³ +24 ;
V3 = 496 = 24 +25 +26 +27 +28 ;
V4 = 8128 = 26 +27 +...+211 +212 ;
V5 = 33550336 = 212 +213 +.. .+224
и т. д.;
б) каждое из известных совершенных чисел, начиная с V2, разлагается на сумму кубов последовательных нечетных чисел:
V2 =28= 1³ +3³ ; V3 = 496=1³ +3³ + 5³ +7³ ;
V4 =8128 =1³ + 3³ + 5³ + 7³ + 9³ + 11³ +13³ +15³ ;
V5 =33550336= 1³ +3³ +... + 127³ и т. д.;
в) складывая цифры каждого из известных совершенных чисел, начиная с V2, и повторяя этот процесс для получающегося результата некоторое количество раз, всегда в конце концов получим число 1:
V2 = 28; 2+8 = 10; 1+0 = 1;
V3 = 496; 4+9+6 = 19; 1+9 = 10; 1+0 = 1;
V4 = 8128; 8+1+2+8=19; 1+9 = 10; 1+0=1;
V5 = 33550336; сумма цифр=28; 2+8=10; 1+0=1 и т. д.;
г) если за основание системы чисел принять не 10, а 2, как это теперь иногда приходится делать для использования электронных вычислительных машин, то совершенные числа принимают такой вид:
по основанию 10
V1 =6=2(2² -1); V2 =28=2² (2³ -1); V3 =496= 24 (25 - 1); V4 = 8128= 26 (27 -1);
по основанию 2
V1 =110 ; V2 = 11 100; V3 =111 110 000; V4 = 1 111 111 000 000 и т. д.
Как видим, в системе с основанием 2 число единичек совпадает с числом р в десятичной записи совершенного числа Vn = 2p-1 (2p - 1), а число нулей равно p-1.
Желающим предлагаем попробовать свои силы в решении следующей трудной задачи, связанной с указанным выше свойством б).
Доказать, что каждое совершенное число вида Vn =2p-1 (2 p -1), начиная с V2, разлагается на сумму кубов нечетных чисел, где количество слагаемых равно 2.
382
в мощности различных множеств. Упомянем лишь одну из них: существует взаимно-однозначное соответствие между всеми точками прямой и всеми точками плоскости.
Заметим, наконец, следующее. В математике наибольшее значение имеют так называемые числовые множества, т. е. множества, элементами которых являются действительные числа. Все известные в настоящее время числовые множества или счетны, или имеют ту же мощность, что и вся числовая прямая. Возникла, таким образом, гипотеза, что всякое несчетное числовое множество имеет ту же мощность, что и вся числовая прямая. Эта гипотеза была высказана еще Кантором и известна под названием континуум-гипотезы. Она не доказана до сих пор, что связано, по-видимому, с большими трудностями, возникающими при рассмотрении произвольных числовых множеств. Трудности эти получают свое освещение в так называемой математической логике, и мы о них здесь, конечно, говорить не можем.
Эта статья имеет своей целью дать лишь начальное представление о некоторых простейших понятиях обширной области математики - теории множеств, области, возникшей менее чем сто лет назад.
В арифметике и алгебре рассматривают числа разной природы - целые числа, рациональные числа (дроби) и другие. Во всех случаях с каждыми двумя числами а и b сопоставляются еще два числа a+b и ab, называемые суммой и произведением чисел а и b. Определение суммы и произведения двух чисел различно для чисел разной природы. Так, если a есть целое положительное число, то его можно представлять себе как число предметов
в некотором наборе. При этом сумма а + b означает число предметов, которое мы получим, если объединим первый набор, содержащий а предметов, и второй набор, содержащий b предметов (рис.1). Если же объединим b наборов, каждый из которых содержит по а предметов, то всего мы получим ab предметов
Более сложно определяются сумма и произведение дробей - например, так:
a1 /a2 +b1 /b2 =(a1 b2 + a2 b1)/a2 b2 и (a1 /a2)(b1 /b2)=a1 b1 /a2 b2 .
Здесь числа a1, a2, b1, b2 - целые. Иные правила относятся к сложению и умножению отрицательных чисел: среди этих правил есть, скажем, такое:
(- а)(- b) =+ ab.
Но независимо от природы рассматриваемых чисел и от определения суммы и произведения чисел общие законы действия над числами остаются одни и те же. Вот эти законы:
а + b = b + a
(коммутативный, или переместительный, закон для сложения);
a b = b a
(коммутативный, или переместительный, закон для умножения);
(а + b) + с = а + (b + с)
(ассоциативный, или сочетательный, закон для сложения);
(a b) c = а (b с)
(ассоциативный, или сочетательный, закон для умножения);
(а + b)с = ас + bc
(дистрибутивный, или распределительный, закон).
При этом сразу бросается в глаза, что правила, относящиеся к сложению чисел, очень похожи на правила умножения.
383
Например:
а+ b = b + a и а b = b а, (а + b)+с=а+(b +с) и (а b)с= а(b с).
Это сходство между действиями сложения и умножения находит отражение и в существовании двух замечательных чисел 0 и 1 -таких, что прибавление одного из них и умножение на второе не меняют ни одного числа: a +0=а и a ·1=а.
Следует, впрочем, заметить, что сходство между действиями сложения и умножения не простирается особенно далеко. Так, например, число 0 играет особую роль не только по отношению к сложению, но и по отношению к умножению: эта особая роль числа 0 определяется замечательным равенством а ·0 = 0. (Из этого равенства, в частности, вытекает, что делить на 0 число а ≠ 0 нельзя.) В противоположность этому, число 1 по отношению к операции сложения не играет никакой особой роли: равенство, которое получается из равенства а · 0 = 0 заменой числа 0 на число 1 и операции умножения - операцией сложения:
а + 1 == 1,
почти никогда не будет верным. (Это равенство справедливо лишь при а = 0.) Также и дистрибутивный закон:
(а + b)с=ас + bc
подчеркивает различие между действиями сложения и умножения. Если заменить в записи этого закона сложение умножением и наоборот, то получим курьезное «равенство»:
(а· b)+с = (а+с)·(b +с),
как правило, не выполняющееся: так, 1·2+3=5, а (1+3)·(2+3)=20. (Равенство (а · b) + с=(а +с)· (b + с) справедливо лишь при с= 0 и при а+ b +с =1.)
В математике, однако, операции сложения и умножения определяются не только для чисел. При этом иногда удается прийти к «алгебре», в которой сходство между операциями сложения и умножения оказывается большим, чем в обычной «числовой» алгебре. В качестве примера можно указать «алгебру множеств».
Рассмотрим систему всевозможных множеств (совокупностей) тех или иных объектов; для конкретности будем все время говорить о множествах учеников нашего класса.
Сумму A + В двух множеств A и B определим как такое множество, которое получается при объединении множеств A и B; другими словами, в множество A + B входят все те, и только те объекты, которые входят в множество A или в множество B. Так, например, если A есть множество отличников из нашего класса, состоящее из учеников Пети, Саши, Кати, Веры и Наташи, а B - множество учеников, сидящих в первом ряду, и состоящее из школьников Ильи, Гриши, Зои, Кати, Наташи и Яши, то сумма A + B этих двух множеств состоит из учеников, которые являются отличниками или сидят в первом ряду; в нее входят ученики Петя, Саша, Катя, Вера, Наташа, Илья, Гриша, Зоя и Яша (рис.3).
То обстоятельство, что мы назвали «сложением» совершенно новую операцию, не должно нас смущать,- ведь мы и раньше каждый раз, когда переходили от чисел одной природы к числам другой природы, определяли сложение по-новому. Ясно, например, что сложение положительных и отрицательных чисел - это не то же самое, что сложение одних положительных чисел; так, сумма чисел 5 и (-3) - это то же самое, что разность чисел 5 и 3. Сложение дробей - не то же самое, что сложение целых чисел; рис.1, изображающий сложение чисел, становится непригоден, когда речь заходит о дробях. Однако, называя уже знакомым нам словом «сложение» новую операцию, мы каждый раз должны были лишь «доучиваться», но не «переучиваться»,- навыки, выработавшиеся в процессе действий с це-
384
Рис.4.
лыми числами, оказываются полезными и при действиях с дробями, правила действий над положительными числами полезны и при действиях с относительными числами и т. д. Это связано с тем, что общие законы, которым подчиняется операция сложения целых чисел, остаются в силе и в дальнейшем, скажем при переходе к дробным числам; так, в обоих случаях сложение коммутативно (т. е. а + b= b+ а) и ассоциативно: (а + b) + с= а +(b +с).
Посмотрим теперь, сохраняют ли силу эти законы и для множеств. При этом нам удобно будет использовать специальные диаграммы, иллюстрирующие действия над множествами. Условимся обозначать весь класс (точнее говоря, множество всех учеников класса) квадратом; в этом квадрате можно расставить ряд точек, по числу учеников (рис.4).
При этом отдельные множества учеников будут изображаться частями квадрата; так, например, изображенная на рис.5, а фигура графически иллюстрирует множество A отличников, а изображенная на рис.5,б - множество В учеников, сидящих в первом ряду. Под суммой двух множеств A и В понимается фигура, получаемая объединением фигур, изображающих множества A и В (рис.6).
Такие диаграммы принято называть диаграммами Эйлера или диаграммами Венна. Они позволяют наглядно представить операцию сложения множеств и проверить ее свойства.
Рис.6. Сумма фигур - это их объединение.
Ясно, например, что A + B = B + A (коммутативный закон для сложения множеств; рис.7).
Также ясно, что (A + B) + C = A + (B + C) (ассоциативный закон для сложения множеств; рис.8). Сумму (A + B)+C = A+(B+C) естественно обозначать просто через A + B + C (без скобок).
Определим теперь произведение A·B или AB двух множеств A и B как множество, получаемое в пересечении множеств A и B; другими словами, в множество AB входят те, и только те, элементы, которые входят как в множество A, так и в множество B. Так, например, если A и B - указанные выше множество отличников и множество учеников, сидящих в классе в первом ряду, то множество AB состоит из тех учеников, которые являются отличниками и сидят в первом ряду; оно состоит всего из двух учеников - Кати и Наташи (рис.9). На рис.10 то же множество AB изображено на диаграмме как пересечение множеств A и B.
Использование термина «произведение» в совершенно новом смысле оправдывается тем обстоятельством, что, как и для обыкновен-
385
Рис.10. Произведение двух фигур - это их пересечение.
ного умножения, мы имеем: AB = BA (коммутативный закон для умножения множеств; рис.11) и (AB)C = A(BC) (ассоциативный закон для умножения множеств; рис.12). Множество (AB)C = A(BC) естественно обозначать просто через A B C (без скобок).
Проверим теперь, выполняется ли для множеств дистрибутивный закон. На рис.13,а заштрихованы множества A + B и C, при этом двойной штриховкой оказывается покрыто множество (A + B) C. На рис.13,б различно заштрихованы AC и BC; при этом как-то заштриховано множество A C + BC. Но легко видеть, что множество, покрытое двойной штриховкой на рис.13,а,- это в точности то множество, которое заштриховано на рис.13,б. Отсюда заключаем: в «алгебре множеств» выполняется дистрибутивный закон:
(A + B)C = AC + BC.
Всем, кто впоследствии пожелает изучить правила алгебры логики, имеет смысл предварительно попрактиковаться в применении своеобразных математических приемов выявления истины из поступившей информации, содержащей в себе и правду, и ложь. Пусть полученная информация состоит из нескольких сообщений, причем заранее известно, что правдиво только какое-то одно. Сейчас несущественно - часто или редко в действительности может оказаться такая ситуация.
Условимся, что эквивалентом всякого верного утверждения будет число 1, а всякого ложного - число 0. Тогда полученные сведения можно определенным образом закодировать (зашифровать) символами и составить из этих символов и чисел 0 и 1 некоторые алгебраические выражения и равенства. При этом каждое утверждение можно представить в двух видах: как произведение и как сумму.
Пусть буквами A и B обозначены два верных утверждения, т. е. каждая буква имеет значение 1; тогда произведение A B = 1; но если A или B ложно, т. е. имеет значение 0, то A · B = 0. Сумму двух верных утверждений (т. е. двух единиц) следует считать равной 1, A + B = 1, так как в нашей алгебре нет чисел, превышающих единицу; в самом деле, ведь ничто не может быть более правильным, чем «верно» Однажды произошел такой разговор:
Мама. Вчера мне сказали, что Саша, сын Николая Ивановича, уже окончил институт, а ему еще только двадцать один год.
Папа. Ты что-то напутала, дорогая. Сына Николая Ивановича зовут Костя, и ему еще только недавно исполнилось восемнадцать.
Дочь. Я не знаю семьи Николая Ивановича, но помню, подруга утверждала, что его сыну 25 лет, и при этом называла она его другим именем, не Сашей.
При помощи вычислений определите имя и возраст сына Николая Ивановича, полагая, что в каждой из полученных информаций содержатся верные сведения либо только о возрасте, либо только об имени. Решение на стр.471.
386
Выясним, существует ли в «алгебре множеств» такой элемент 0 «нуль», что прибавление его к любому множеству A не меняет этого множества. Ясно, что последнее возможно только в том случае, если «множество 0» совсем не содержит элементов, является «пустым». Но в последнем случае не хочется даже говорить о «множестве», какое же это множество, состоящее из отдельных элементов, если этих элементов вовсе нет?
В учении о множествах, однако, целесообразнее причислять пустое множество, вовсе не содержащее элементов, к числу рассматриваемых множеств. Ведь в противном случае мы зачастую не сможем говорить о множестве, не выяснив предварительно, существует оно или нет. Так, прежде чем сказать: «Множество отличников из IX «а» класса школы № 13 Ленинграда», - нам придется пойти в школу и справиться об успеваемости учеников этого класса. Гораздо удобнее спокойно говорить об этом множестве, оговорив только, что оно может быть и «пустым», т. е. не содержать ни одного элемента. В ряде случаев мы можем заранее сказать, что то или иное множество не является пустым; так, не пустое, разумеется, множество самых высоких учеников класса (это множество может иногда содержать и больше одного ученика). В иных случаях мы сразу скажем, что множество, о котором идет речь,- пустое. Так, конечно, пустым является множество обучающихся в нашем классе живых слонов или множество учеников, имеющих две головы. Однако в большинстве случаев лишь более тщательный анализ позволяет указать, является то или иное множество пустым или нет. Так, например, множество Семенов или множество левшей из нашего класса может быть пустым или не пустым. Пустое множество в дальнейшем всегда будем обозначать знаком 0. Таким образом, для каждого множества A будем иметь (рис.14):
A + 0 = A.
Подобно известному правилу а · 0 = 0 алгебры чисел, для любого множества A:
A · 0 = 0.
В самом деле, множество A · 0, по определению, состоит из всех элементов, принадлежащих и множеству A и множеству 0. Но множество 0 вовсе не содержит элементов и не может содержать элементов и множество A · 0.
Теперь зададимся вопросом о «множестве 1», обладающем тем свойством, что произведение его на любое множество A дает A. Последнее означает, что пересечение или общая часть «множества 1» и множества A для любого множества A совпадает с самим этим множеством. Но это возможно, разумеется, лишь в том случае, если «множество 1» содержит все вообще существующие элементы. Так, если мы рассматриваем всевозможные множества учеников из нашего класса, то роль единицы будет играть множество всех обучающихся в классе учеников. Нетрудно понять, что, скажем, произведение этого множества и множества A будет состоять из всех отличников (т. е. совпадать с A); произведение этого множества и множества B будет состоять из всех учеников, сидящих в первом ряду (т. е. будет совпадать с множеством B).
Множество, состоящее из всех элементов всех рассматриваемых множеств, называется полным, универсальным, или единичным; мы будем обозначать его знаком I. Таким образом, для любого множества A: A · I = A.
Универсальное множество I графически изображается всем квадратом, внутри которого мы рисуем фигуры, изображающие различные множества (рис.15).
До сих пор все рассматриваемые законы действий над множествами совпадали с законами действий над числами. Однако на самом деле алгебра множеств вовсе не копирует в точности алгебру чисел; она обладает и многими удивительными свойствами, не имеющими места в обычной алгебре. Мы начнем со второго дистрибутивного закона, получаемого из первого дистрибутивного закона: (A+B)C = AC+BC заменой сложения умножением и наоборот:
AB+C = (A+C) (B+C).
387
Как уже указывалось, в алгебре чисел этот второй дистрибутивный закон, вообще говоря, места не имеет. По-другому обстоит дело с алгеброй множеств. На рис.16,а заштрихованы множества AB и C, так что заштриховано на этом рисунке множество AB + C. На рис.16,б заштрихованы множества A + C и B + C, так что двойной штриховкой покрыто множество (A + C)(B + C). Но легко видеть, что множество, покрытое на рис.16,б двойной штриховкой, - это в точности то множество, которое заштриховано на рис.16,а. Таким образом, для любых трех множеств A, B и C:
AB+C = (A + C) (B + C).
Далее, выше мы отмечали курьезное равенство: а+1=1, получаемое из равенства а·0=0 заменой нуля единицей и умножения сложением. Но курьезным это равенство является лишь в алгебре чисел. В алгебре же множеств, очевидно, для любого множества A:
A + I = I.
В самом деле, сумма A + I представляет собой множество, получаемое объединением универсального множества I и множества A. Но уже множество I содержит все имеющиеся в нашем распоряжении элементы, так что прибавление к нему множества A ничего изменить не может: сумма A + I - это то же самое универсальное множество I !
Отметим еще необычные равенства:
A + A = A и A · A = A,
также выполняющиеся для каждого множества A. В самом деле, сумма A+A представляет собой объединение множества A с самим собой. Но при этом мы придем к тому же самому множеству A (рис.17). Аналогично этому произведение AA есть пересечение множества A с самим собой, но это пересечение не отличается от множества A (см. тот же рис.17).
Последние два равенства можно еще обобщить. Различные множества можно сравнивать друг с другом. Естественно считать, что множество A «больше» множества B, если все элементы множества B содержатся в множестве A. Это соотношение записывается так: A  B или B
B или B 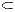 A; при этом говорят, что «множество A содержит множество B» или «множество B содержится в множестве A». Так, множество C девочек, сидящих в первом ряду (это множество состоит из школьниц Зои, Кати и Наташи), содержится в множестве B учеников, сидящих в первом ряду: B
A; при этом говорят, что «множество A содержит множество B» или «множество B содержится в множестве A». Так, множество C девочек, сидящих в первом ряду (это множество состоит из школьниц Зои, Кати и Наташи), содержится в множестве B учеников, сидящих в первом ряду: B  C (рис.18). Графически соотношение A
C (рис.18). Графически соотношение A  B изображается тем, что фигура B целиком заключается в фигуре A (рис.19) или B совпадает с A 1. Ясно, что если A
B изображается тем, что фигура B целиком заключается в фигуре A (рис.19) или B совпадает с A 1. Ясно, что если A  B и B
B и B  C, то A
C, то A  C (рис.20); это утверждение аналогично известному свойству неравенств: если а > b и b > с, то а > с.
C (рис.20); это утверждение аналогично известному свойству неравенств: если а > b и b > с, то а > с.
Нетрудно видеть, что если A  B, то A+B = A; AB = B
B, то A+B = A; AB = B
1 Соотношение A  B, строго говоря, переносит в алгебру множеств не соотношение а > b алгебры чисел, а соотношение а ≥ b («число a больше или равно b»).
B, строго говоря, переносит в алгебру множеств не соотношение а > b алгебры чисел, а соотношение а ≥ b («число a больше или равно b»).
388
(рис.21а,б). Так как можно считать, что A  A, то отсюда вытекают и два выписанных ранее равенства:
A, то отсюда вытекают и два выписанных ранее равенства:
A+A = A и AA = A.
Мы видим, что правила алгебры множеств во многом отличны от правил алгебры чисел. Поэтому, для того чтобы овладеть этой удивительной алгеброй, приходится не только «доучиваться», но частично и «переучиваться»- отказываться от некоторых привычных представлений, связанных с опытом действий с числами.
Вот, например, одно из многих необычных, с точки зрения алгебры чисел, тождеств:
(A+C)(B+C)A=AB+CA,
(рис.22,а и б).
Укажем теперь еще одно отличие алгебры множеств от алгебры чисел, которое читатель, возможно, и не отметил. Имея дело с числами, мы можем сравнить между собой любые два числа a и b: всегда одно из них больше другого (или эти числа равны). Для двух множеств A и B, однако, как правило, не будет иметь место ни одно из двух соотношений A  B и B
B и B  A. Так, в случае указанных выше множества A отличников и множества B учащихся, сидящих в первом ряду, ни одно из этих множеств нельзя считать большим. Только если одно из двух множеств целиком содержится внутри другого, мы можем указать большее из них; для других же множеств A и B, графически изображенных на рис.23,а и б, никакое сравнение их невозможно. Таким образом, лишь для некоторых пар множеств A и B можно указать, какое из этих множеств является большим.
A. Так, в случае указанных выше множества A отличников и множества B учащихся, сидящих в первом ряду, ни одно из этих множеств нельзя считать большим. Только если одно из двух множеств целиком содержится внутри другого, мы можем указать большее из них; для других же множеств A и B, графически изображенных на рис.23,а и б, никакое сравнение их невозможно. Таким образом, лишь для некоторых пар множеств A и B можно указать, какое из этих множеств является большим.
Алгебра множеств с ее своеобразными законами действий, одновременно и напоминающими правила действий над числами, и отличными от этих правил, была впервые указана замечательным английским математиком прошлого века Дж. Булем, отцом известной писательницы Этель Лилиан Войнич (автора романа «Овод»). По имени Буля алгебру множеств часто называют «булевой алгеброй».
Основополагающее сочинение Буля, в котором впервые строилась булева алгебра, называлось «Исследование законов мысли»; оно было напечатано в Лондоне в 1854 г., т. е. более ста лет назад. Название книги Буля сначала может показаться удивительным,- какое отношение имеет курьезная алгебра множеств к законам нашего мышления? На этот вопрос мы постараемся ответить ниже.
Поскольку законы действий над множествами отличаются от законов действий над числами, иногда считают, что эти действия нельзя обозначить теми же символами, которые используются в алгебре чисел. В математической литературе сумма множеств A и B часто обозначается через A 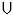 B, а произведение этих же множеств через A ∩ B. При этом правила действий булевой алгебры множеств записываются в следующем виде:
B, а произведение этих же множеств через A ∩ B. При этом правила действий булевой алгебры множеств записываются в следующем виде:
A 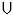 B = B
B = B  A,
A,
A ∩ B = B ∩ A
(коммутативные законы);
389
Джордж Буль.
(A  B)
B)  C = A
C = A 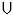 (B
(B  C,
C,
(A ∩ B) ∩ C = A ∩ (B ∩ C)
(ассоциативные законы);
(A  B) ∩ C = (A ∩ C)
B) ∩ C = (A ∩ C)  (B ∩ C),
(B ∩ C),
(A ∩ B) 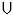 C = (A
C = (A  C) ∩ (B
C) ∩ (B  C)
C)
(дистрибутивные законы);
A  0 = A,
0 = A,
A ∩ I = A,
A ∩ 0 = 0,
A 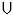 I = I,
I = I,
A  A = A,
A = A,
A ∩ A = A.
Мы, однако, предпочтем во всех случаях пользоваться знакомыми символами сложения и умножения.
Вернемся к установленным выше свойствам действий алгебры множеств. Сразу бросается в глаза чрезвычайно тесная связь между законами, относящимися к сложению множеств, и законами умножения. Выпишем снова эти законы:
A+B=B+A, AB=BA;
(A+B)+C=A+(B+C), (AB)C=A(BC);
(A+B)C=AC+BC, AB+C=(A+C) (B+C);
A + 0 = A, AI = A;
A + I = I, A0 = 0;
A+A = A, AA = A
и т. д. Из этой таблицы видно, что всякое равенство, тождественно выполняющееся в алгебре множеств, при замене знака сложения множеств знаком умножения, и наоборот, и пустого множества 0 (если оно входит в наше равенство) универсальным множеством I, и наоборот, переходит в новое равенство, также тождественно выполняющееся.
Сейчас мы докажем это утверждение в общем виде. Для этого нам понадобится одна своеобразная операция алгебры множеств, сопоставляющая новое множество не с двумя заданными множествами (подобно сумме A + B и произведению AB заданных множеств), а с одним множеством A. Эта операция называется образованием дополнения и обозначается чертой, поставленной над множеством. А именно, через Ā [1] (читается: «дополнение A») мы будем обозначать множество всех элементов универсального множества I, не принадлежащих множеству A. Так, если A есть множество отличников из нашего класса, то множество Ā состоит из всех учеников, не являющихся отличниками. На диаграмме множество Ā изображается частью квадрата I, не покрытой фигурой A (рис.24). Ясно, что A + Ā = I, A Ā = 0 (см. тот же рис.24, на котором графически изображены множества A и Ā); эти два равенства можно даже принять за определение множества Ā.
Отметим еще, что (Ā)¯ = A (рис.25). Это последнее равенство короче записывают так:
Очевидно, что I¯ = 0 и Ō = I (так как все элементы входят в универсальное множество I и ни один элемент не входит в пустое множество 0). Кроме того, легко видеть, что
если A  B, то B¯
B, то B¯  A¯ (рис.),
A¯ (рис.),
т.е. если множество B составляет часть множества A, то дополнение A составляет часть дополнения B (рис.26,а,б):
[1] - в печатном тексте придется иногда верхнюю черточку ставить не над буквой, а следом: A¯, I¯. Чтобы отобразить черточку над выражением, выражение будем заключать в скобки, а черточку помещать следом за скобками, по аналогии с записью показателя степени. - Прим.оцифровщика.
390
Докажем теперь следующие два важные соотношения:
(A + B)¯ = A¯B¯ и (AB)¯ = A¯ + B¯,
или словами: дополнение суммы двух множеств совпадает с пересечением дополнений этих множеств; дополнение произведения двух множеств совпадает с суммой дополнений этих множеств.
B самом деле, на рис. 27,а заштрихованы множества A и B, а на рис. 27,б - их дополнения A¯ и B¯. Но ясно, что фигура, заштрихованная на рис. 27,а, является дополнением до всего квадрата I фигуры, покрытой на рис. 27,б двойной штриховкой, т. е. фигура (AB)¯; это и доказывает равенство (A + B)¯ = A¯B¯. Аналогично, фигура, покрытая на рис. 27,а двойной штриховкой, дополняет до всего квадрата фигуру, заштрихованную на рис. 27,б, откуда следует, что (AB)¯ = A¯ + B¯.
Из доказанных соотношений нетрудно вывести наше утверждение, позволяющее по каждому соотношению алгебры множеств построить новое соотношение- Рассмотрим какое угодно тождество алгебры множеств, например первый дистрибутивный закон:
(A + B)C = AC + BC.
Так как множества (A + B)C и AC + BC совпадают, то совпадают и дополнения этих множеств:
((A + B)C)¯ = (AC + BC)¯.
Но мы знаем, что (AB)¯ = A¯ + B¯; поэтому
((A + B)C)¯ = (A + B)¯ + C¯.
С другой стороны, нам известно, что
(A + B)¯ = A¯B¯.
Таким образом,
((A + B)C)¯ = A¯B¯ + C¯.
Далее, в силу того же закона (A + B)¯ = A¯B¯. алгебры множеств, имеем:
(AC + BC)¯ = AC¯ · BC¯.
Но AC¯ = A¯ + C¯ и BC¯ = B¯ + C¯; поэтому
(AC + BC)¯ = (A¯ + C¯)(B¯ + C¯).
Таким образом, мы приходим к равенству:
A¯B¯ + C¯ = (A¯ + C¯)(B¯ + C¯),
которое, очевидно, лишь по форме отличается от второго дистрибутивного закона:
AB + C = (A + C)(B + C),
где вместо самих множеств A, B и C выступают их дополнения A¯, B¯ и C¯. Но это совершенно несущественно, поскольку как сами рассматриваемые множества, так и их дополнения произвольны. Таким образом, с помощью образования дополнения мы вывели из первого дистрибутивного закона второй дистрибутивный закон.
Точно таким же путем можно из любого тождества алгебры множеств получить другое тождество, в котором всюду операция сложения заменена умножением, и наоборот. При этом если в первоначальное тождество входили множества 0 и I, то в новом тождестве они заменяются соответственно на I и 0: это связано с тем, что 0¯ = I и I¯ = 0.
Поставим теперь вопрос о том, каким образом можно задать то или иное множество. Проще всего это сделать, перечислив псе элементы, в совокупности составляющие данное множество: так, можно сказать, что фигурирующее выше множество A состоит из школьников Пе-
391
ти, Саши, Кати, Веры и Наташи. Однако в тех случаях, когда множество содержит много элементов, этот явный, или перечислительный, способ задания множества может оказаться очень неудобным. Кроме того, при таком задании множества обычно оказывается замаскированным самый принцип его образования, то общее, что служит причиной объединения отобранных элементов в одно множество.
Второй способ задания множества состоит в том, что мы указываем признак, характеризующий все элементы множества, и только эти элементы. Так, выше мы говорили: «множество отличников» или «множество учащихся, сидящих в классе в первом ряду». Такой способ задания множества называется неявным или описательным. Этот способ заключается в том, что мы формулируем некоторое высказывание, касающееся элементов рассматриваемого универсального множества / («быть отличником» или «сидеть в первом ряду»); далее отбираем те, и только те, элементы множества I, которые этому высказыванию удовлетворяют.
Описательный способ задания множества связывает учение о множествах с учением о высказываниях, составляющим предмет математической логики. Высказыванием мы называем всякое утверждение, которое может оказаться истинным или ложным; при этом предполагается, что в принципе существует возможность установить, истинно данное высказывание или ложно, хотя мы, быть может, этой возможности не имеем. С этой точки зрения утверждение «ровно через 100 лет в этот день в Москве будет ясная погода» является высказыванием, поскольку через 100 лет можно будет проверить, правда это или нет. Напротив, утверждение «неделя - это большой промежуток времени» высказыванием не является в силу неопределенности выражения «большой промежуток времени», которое у разных лиц и в различных обстоятельствах может иметь совершенно разный смысл; здесь, не обладая несколькими дополнительными сведениями, никак нельзя сказать, является это утверждение истинным или нет.
Рассмотрим теперь высказывания, относящиеся к элементам определенного универсального множества I; в случае, когда этим множеством является множество учащихся данного класса, это могут быть высказывания: «он отличник», «он сидит в первом ряду», «он выше 1 м 50 см», «он старше 50 лет», «он - это девочка», «он левша», «он имеет две головы» и т. д.
Каждому такому высказыванию отвечает некоторое множество элементов из I, для которых это высказывание является истинным; это множество называется множеством истинности данного высказывания. Множество истинности может оказаться пустым; в этом случае высказывание называется тождественно ложным или противоречивым. Так, для множества учеников данного класса тождественно ложными будут высказывания «он имеет две головы» или «ему больше 50 лет»; выше у нас фигурировало еще одно высказывание, также заведомо противоречивое в применении к ученикам какого-либо класса: «он слон». В определенном смысле противоположный случай - это тот, когда множество истинности данного высказывания совпадает со всем универсальным множеством I; в этом случае высказывание называется тождественно истинным или бессодержательным. Тождественно истинными являются, например, высказывания: «он (ученик определенного класса) моложе 50 лет», «он мальчик или девочка».
Высказывания мы будем обозначать малыми буквами латинского алфавита; отвечающие этим высказываниям множества истинности будем обозначать большими буквами. Так, высказываниям a - «он отличник» и b - «он сидит в первом ряду» отвечают указанные выше множества истинности A и B. Тождественно ложное высказывание всегда будем обозначать буквой о, а тождественно истинное высказывание - буквой i.
Рассмотрим теперь две операции, позволяющие по двум высказываниям строить новые, составные высказывания. В математической логике эти операции называются латинскими терминами «дизъюнкция» и «конъюнкция» и обозначаются специальными значками  и
и  ; так, a
; так, a  b означает дизъюнкцию высказываний a и b, а
b означает дизъюнкцию высказываний a и b, а  b - конъюнкцию (сравним с обозначениями суммы и произведения, или объединения и пересечения, множеств, указанными на стр. 389). Мы здесь для простоты почти не будем употреблять этих сложных терминов и символов; вместо этого будем говорить о сумме a + b и произведении а b высказываний a и b .
b - конъюнкцию (сравним с обозначениями суммы и произведения, или объединения и пересечения, множеств, указанными на стр. 389). Мы здесь для простоты почти не будем употреблять этих сложных терминов и символов; вместо этого будем говорить о сумме a + b и произведении а b высказываний a и b .
392
Под суммой (дизъюнкцией) высказываний a и b понимается высказывание, которое мы получим, если объединим высказывания a и b союзом «или». Например, если a есть высказывание «он отличник», а b - высказывание «он сидит в первом ряду», то через a+b будем обозначать высказывание «он является отличником или сидит в первом ряду». При этом частичку «или» мы будем всегда понимать в смысле: «или первое, или второе, или то и другое вместе». Ясно, что если A есть множество истинности высказывания a, а B - множество истинности высказывания b, то множеством истинности высказывания a + b будет A + B (рис.28). Так, в рассматриваемом примере множество истинности высказывания a состоит из школьников Пети, Саши, Кати, Веры и Наташи, а множество истинности высказывания b - из школьников Ильи, Гриши, Зои, Кати, Наташи и Яши; множество же истинности высказывания a + b образуют девять школьников: Петя, Саша, Катя, Вера, Наташа, Илья, Гриша, Зоя и Яша.
Под произведением (конъюнкцией) высказываний a и b мы будем понимать высказывание ab, получаемое, если объединить высказывания a и b, связав их союзом «и». Итак, множеством истинности высказывания ab является произведение (пересечение) множеств истинности высказываний a и b (рис.29). В нашем примере это множество ab состоит из двух учениц - Кати и Наташи.
Условимся еще называть два высказывания одинаковыми, или эквивалентными, если им отвечает одно и то же множество истинности. Эквивалентность высказываний будем обозначать обычным знаком равенства. Равенство а= b означает, что содержащиеся в высказываниях a и b признаки, выделяющие определенную часть универсального множества, равнозначны, имеют один и тот же смысл, разнятся только своей формой. При изучении высказываний естественно не различать между собой эквивалентные высказывания, например «он отличник» и «он имеет отличные оценки».
Мы установили, что множество истинности суммы двух высказываний совпадает с суммой множеств истинности этих высказываний; множество истинности произведения двух высказываний совпадает с произведением множеств истинности этих высказываний. Отсюда следует, что все известные нам правила алгебры множеств можно перевести на язык алгебры высказываний. Так, например:
a + b = b + a, ab = ba;
(a+b)+c = a+ (b+ с), (ab)c = a(bc);
(a + b)c = aс+ bc, ab+ с = (a+ c)(b+ c);
a+0 = a, aI = a;
a·0 = 0, a+I = I ;
a+a = a, aa = a и т. д.
Докажем для примера первый дистрибутивный закон для высказываний, т. е. равенство:
(a + b) c = ac + bc.
В соответствии с нашим условием множества истинности высказываний a, b и c обозначаются через A, B и C. При этом высказывание (a + b)c имеет своим множеством истинности (A + B)C; высказывание ac + bc имеет своим множеством истинности AC + BC. Но множества (A + B)C и AC + BC совпадают; это значит, что высказывания (a + b)c и ac + bc эквивалентны.
Запишем еще законы алгебры высказываний в той форме, в которой они приводятся в книгах по математической логике:
a b = b
b = b а,
а,
(а b)
b) с = a
с = a (b
(b с),
с),
(а b)
b) с = (а
с = (а с)
с) (b
(b с),
с),
a b = b
b = b a,
a,
(а b)
b) с = а
с = а (b
(b с),
с),
(а b)
b) с = (а
с = (а с)
с) (b
(b с).
с).
а 0 = а, a
0 = а, a I = а,
I = а,
а 0 = 0, а
0 = 0, а I = I,
I = I,
a а = а, а
а = а, а а = а.
а = а.
393
Продолжим построение алгебры высказываний. При изучении множеств мы наряду с операциями сложения и умножения множеств рассматривали также операцию «взятия дополнения», сопоставляющую с каждым множеством A его дополнение A¯. Этой операции отвечает чрезвычайно важная операция алгебры высказываний, сопоставляющая с каждым высказыванием a новое высказывание a¯, называемое отрицанием a. Грамматически высказывание a¯ (отрицание a) получается из высказывания a при помощи частицы «не»; например, отрицанием высказывания «он отличник» является высказывание «он не отличник». Множество истинности высказываний a¯ является дополнением множества истинности высказывания a (рис .30); это утверждение можно даже считать определением отрицания.
Алгебраические свойства дополнения множеств сразу приводят к. следующим утверждениям, связанным с отрицанием высказываний:
a + a¯ = i, aa¯ = о;
i¯ = о, о¯ = i;
(a¯)¯ = a;
(a + b)¯ = a¯b¯, (ab)¯ = a¯ + b¯.
Введем, наконец, отношение  , связывающее два высказывания. А именно- будем писать a
, связывающее два высказывания. А именно- будем писать a b (или b
b (или b a) и говорить, что высказывание a следует из высказывания b или a является следствием b, если множество истинности A высказывания a содержит множество истинности B выскааывавия b, т. е. если A
a) и говорить, что высказывание a следует из высказывания b или a является следствием b, если множество истинности A высказывания a содержит множество истинности B выскааывавия b, т. е. если A B (или B
B (или B A).
A).
Например, если множество отличников класса состоит из школьников Гриши, Ильи и Пети, то высказывание «он мальчик» является следствием высказывания «он отличник» (рис. 31). Отношение следствия имеет следующий смысл: если а b, и мы знаем, что высказывание b истинно, то, наверное, истинно и высказывание а. Так. в разобранном выше примере истинность утверждения «он отличник» означает, что речь идет об одном из трех школьников - Грише, Илье или Пете; но тогда истинно и высказывание «он мальчик».
b, и мы знаем, что высказывание b истинно, то, наверное, истинно и высказывание а. Так. в разобранном выше примере истинность утверждения «он отличник» означает, что речь идет об одном из трех школьников - Грише, Илье или Пете; но тогда истинно и высказывание «он мальчик».
Из известных свойств алгебры множеств, связанных с отношением  , следует, что:
, следует, что:
если a b и b
b и b c, то a
c, то a c;
c;
если a b, то a + b = а, аb = b;
b, то a + b = а, аb = b;
если a b, то a¯
b, то a¯ b¯.
b¯.
Теперь мы можем ответить на вопрос о том, почему сочинение Дж. Буля, в котором впервые строилась булева алгебра, посвящено выяснению «законов мысли». Дело в том, что правила алгебры высказываний есть те законы, которые играют руководящую роль в процессе нашего мышления.
Многие из этих законов в логике имеют специальные названия. Например, соотношение
a + a¯ = i
выражает так называемый закон исключенного третьего. Этот закон можно сформулировать так: сумма каждого утверждения и его отрицания тождественно истинна, другими словами, высказывание или его отрицание всегда истинно. Например, тождественно истинно утверждение «он отличник или он не отличник». Другими словами, для каждого элемента универсального множества обязательно справедливо либо высказывание a, либо его отрицание a¯, третьего не дано. Соотношение
а¯·а = o
выражает закон противоречия. Согласно этому закону, ни для одного объекта не может быть одновременно верно и утверждение a, и его отрицание a¯. Например, ни один ученик не может одновременно являться и отличником, и не отличником. Но если высказывания a и a¯ не могут быть истинны одновременно, то произведение a·a¯ тождественно ложно, т. е. множество истинности высказывания a·a¯ пусто. Соотношение
(а¯)¯ = а
выражает хорошо известный закон двойного отрицания. Этот закон утверждает, что отрицание отрицания совпадает с исходным высказыванием. Так, отрицанием высказывания «этот ученик - мальчик» является утверждение «этот ученик-девочка», а двойное отрицание «этот ученик не девочка» возвращает нас к первоначальному высказыванию «этот ученик - мальчик».
Аналогичный характер имеют и все остальные правила алгебры высказываний, устанавливающие эквивалентность (равносильность) тех или иных утверждений. Проиллюстрируем это на нескольких примерах.
Первый дистрибутивный закон утверждает, что высказывания (а + b)с и ас + bc - это одно и то же. Пусть
a есть высказывание «он (ученик) умеет играть в шахматы»,
b - «он умеет играть в шашки» и
c - «он отличник».
В таком случае высказывание (а + b)с имеет следующий смысл: «он умеет играть в шахматы или в шашки и, кроме того, он отличник», а высказывание ас + bc - смысл: «он умеет играть в шахматы и является отличником, либо он умеет играть в шашки и является отличником». Но ясно, что эти два высказывания по существу означают одно и то же.
Второй дистрибутивный закон означает, что эквивалентны два высказывания ab + c и (а + с) (b - c). Если высказывания a, b и c имеют тот же смысл, что и выше, то высказывание ab + c означает: «он умеет играть в шашки и в шахматы или является отличником». Высказывание (a + c)(b + c) имеет следующий смысл: «он умеет играть в шахматы или является отличником; одновременно с этим он умеет играть в шашки или является отличником». Но нетрудно понять, что последнее высказывание по существу совпадает с первым - ведь если ученик, о котором здесь идет речь, не является отличником, то он обязательна умеет играть и в шахматы, и в шашки.
Наконец, остановимся еще на так называемых правилах де Моргана:
(a + b)¯ = a¯b¯ и (ab)¯ = a¯ + b¯
(они называются так по имени английского логика XIX в. А. де Моргана, впервые установившего эти правила). Пусть, например,
a - это высказывание «он умеет играть в шахматы»,
b - «он умеет играть в шашки».
В таком случае сложное высказывание (a + b)¯ есть отрицание того, что ученик умеет играть в шахматы или в шашки. Но это отрицание, очевидно, эквивалентно утверждению о том, что ученик не умеет играть ни в шахматы, ни в шашки, т.е. высказыванию a¯b¯. Аналогично отрицание утверждения о том, что ученик умеет играть и в шахматы, и в шашки (т. е.
Сумма двух дробей (5⁄8)2 + 3⁄8 не изменится, если показатель степени от первой дроби перескочит на вторую.
Действительно,
(5⁄8)2 + 3⁄8 = 5⁄8 + (3⁄8)2
Если вы подметите некоторую закономерность, связывающую знаменатель с числителями данных дробей, то легко подберете еще несколько Аналогичных равенств вида:
(a⁄b)2 + c⁄b = a⁄b + (c⁄b)2
Как зависят a и c от b?
Ответ на стр.500.
Беру две дроби, каждую возвожу в квадрат, результаты складываю, получаю некоторое число S.
Теперь каждую из первоначальных дробей возвожу в куб, результаты складываю и ... получаю то же самое число S.
Выходит, что сумма квадратов двух чисел равна сумме кубов тех же чисел. Такое заключение кажется неправдоподобным. И все же это не фокус, не трюк. Есть много пар таких дробей. Попробуйте найти их.
Решение на стр.500.
высказывание (ab)¯), равносильно утверждению о том, что он не умеет играть в шахматы или не умеет играть в шашки; но это и есть высказывание a¯ + b¯.
В заключение скажем еще несколько слов о правилах, связанных с употреблением соотношения  .
.
Установление того, что два высказывания a и b связаны соотношением a b, называется выводом; при этом высказывание b называется условием, а высказывание a - следствием. С выводами такого рода мы все время встречаемся в науке и в практической жизни; так, например, заключение любой теоремы является следствием ее условия. Правильность вывода обеспечивается соблюдением определенных правил логики. Эти правила логики могуг быть обоснованы с помощью соотношений алгебры высказываний.
b, называется выводом; при этом высказывание b называется условием, а высказывание a - следствием. С выводами такого рода мы все время встречаемся в науке и в практической жизни; так, например, заключение любой теоремы является следствием ее условия. Правильность вывода обеспечивается соблюдением определенных правил логики. Эти правила логики могуг быть обоснованы с помощью соотношений алгебры высказываний.
Известное уже нам соотношение: если a b и b
b и b c, то b
c, то b c, читается так: если из b следует a и из c следует b, то из с следует а. Это соотношение используется в рассуждениях весьма часто. Например, поскольку теорема «сумма углов треугольника равна 180°» вытекает из аксиомы параллельных линий, а теорема «внешний угол треугольника равен сумме внутренних углов, не смежных с ним», вытекает из теоремы о сумме углов треугольника, можно также сказать, что теорема о внешнем угле треугольника является следствием аксиомы параллельных.
c, читается так: если из b следует a и из c следует b, то из с следует а. Это соотношение используется в рассуждениях весьма часто. Например, поскольку теорема «сумма углов треугольника равна 180°» вытекает из аксиомы параллельных линий, а теорема «внешний угол треугольника равен сумме внутренних углов, не смежных с ним», вытекает из теоремы о сумме углов треугольника, можно также сказать, что теорема о внешнем угле треугольника является следствием аксиомы параллельных.
Соотношение: если a b, то b¯
b, то b¯ a¯, - читается так: если из высказывания b следует высказывание a, то из отрицания высказывания a вытекает отрицание высказывания b. Это обстоятельство лежит в основе весьма распространенного метода вывода (или доказательства) «от противного».
a¯, - читается так: если из высказывания b следует высказывание a, то из отрицания высказывания a вытекает отрицание высказывания b. Это обстоятельство лежит в основе весьма распространенного метода вывода (или доказательства) «от противного».
Пусть мы хотим доказать теорему (рис. 32): если соответственные углы. AKM и CLM, образованные прямыми AB и CD с секущей MN, равны между собой (это есть утверждение a), то прямые AB и CD параллельны (зто есть утверждение b).
Вместо того чтобы доказывать соотношение a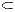 b, докажем, что a¯
b, докажем, что a¯ b¯, т. е. что из отрицания b вытекает отрицание a. Предположим, что прямые AB и CD не параллельны, т.е. что они пересекаются в некоторой точке P (рис. 33, а,б).
b¯, т. е. что из отрицания b вытекает отрицание a. Предположим, что прямые AB и CD не параллельны, т.е. что они пересекаются в некоторой точке P (рис. 33, а,б).
В таком случае углы AKM и CLM не будут равны (это - внешний угол треугольника PKL и не смежный с ним внутренний угол). Таким образом, соотношение a¯ b¯ доказано; тем самым доказано и соотношение a
b¯ доказано; тем самым доказано и соотношение a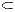 b (строго говоря, здесь надо применить к соотношению a¯
b (строго говоря, здесь надо применить к соотношению a¯ b¯ рассматриваемое предложение алгебры логики и воспользоваться законом двойного отрицания: если a¯
b¯ рассматриваемое предложение алгебры логики и воспользоваться законом двойного отрицания: если a¯ b¯, то (a¯)¯
b¯, то (a¯)¯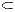 (b¯)¯, т. е. a
(b¯)¯, т. е. a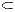 b).
b).
Уже эти примеры показывают ту большую роль, которую играют в любой научной теории правила алгебры логики. В последние годы роль этих правил особенно сильно возросла в связи с возникшей задачей передачи целого ряда операций, выполняющихся людьми, электронным вычислительным машинам. При этом оказалось необходимым научить машину правилам ЛОГИКИ, т. е. тем правилам, которыми люди обычно пользуются, зачастую не отдавая себе полного отчета в существе этих правил. Но для того чтобы ЭТИ правила могли быть заложены в «электронную память» машины, необходимо четко сформулировать их. Эти четкие формулировки и доставляет нам математическая логика.
С симметрией приходится иметь дело не только физикам и кристаллографам, но и художникам, работающим в области прикладного искусства.
Выберем в пространстве некоторую точку Р и рассмотрим различные отрезки РА, РВ, PC ,..., начало которых расположено в точке Р, а концы - в каких-либо точках А, В, С,.. пространства (рис.1). Таким образом, на каждом из этих отрезков выделяется определенное направление, идущее от точки Р (общего начала всех рассматриваемых отрезков) к концу отрезка. По этой при-
Рис.2. Величину и направление силы можно изобразить вектором.
чине они называются не просто отрезками, а направленным и отрезками, приложенными в заданной точке Р; чтобы подчеркнуть это обстоятельство их обозначают
P А→, РВ→, PC→ ,...,
т. е. над отрезком проставляют стрелку. Принято также называть каждый направленный отрезок коротким словом «вектор».
Интерес к векторам возник в науке уже очень давно. Еще в самом начале XVII в. голландский ученый С. Стевин использовал векторы для наглядного представления сил. Так как каждая сила, приложенная к некоторой точке Р твердого тела, имеет вполне определенное направление, то для геометрического изображения этой силы удобно воспользоваться лучом РР', имеющим то же. направление, что и сила; отложим на этом луче от точки Р
направленный отрезок РА, длина которого (выраженная, скажем, в мм) равна числу, которое измеряет величину рассматриваемой силы (выраженную, скажем, в кГ). Таким образом, каждая сила, приложенная в точке твердого тела, изобразится своим вектором (рис.2).
Чтобы прибавить к вектору РА → (первое слагаемое) вектор РВ → (второе слагаемое), поступим следующим образом (рис.3): а) построим середину С отрезка АВ; б) построим точку Q, симметричную точке Р относительно точки С, т. е. так расположенную на луче PC, что точка С является серединой отрезка PQ. Полученный вектор PQ → будем называть суммой векторов РА → (первое слагаемое) и РВ → (второе слагаемое); будем это кратко записывать формулой:
397
Рис.3. Сложение векторов по правилу середины: PQ → = PA → + РВ → .
pa → +pb → =pq →. (1)
Описанное правило сложения векторов назовем правилом середины.
Если слагаемые векторы РА → и РВ → не лежат на одной прямой, то, как легко видеть из
рис.4, вектор PQ →, являющийся их суммой,
Рис.4. Сложение векторов по правилу параллелограмма: PQ → = PA → + PB → .
представляет собой диагональ параллелограмма, сторонами которого являются векторы РА → и РВ → (в самом деле, в четырехугольнике PAQB диагонали АВ и PQ делят друг друга пополам,- это непосредственно вытекает из правила середины).
Таким образом, для сложения векторов РА и РВ, не лежащих на одной прямой, можно вместо правила середины воспользоваться следующим правилом: строим параллелограмм PAQB, сторонами которого являются векторы-слагаемые РА и РВ, т. е. из конца A первого слагаемого строим прямую, параллельную второму слагаемому, а из конца B второго слагаемого строим прямую, параллельную первому слагаемому. Точка Q пересечения построенных прямых и будет концом вектора PQ, являющегося суммой слагаемых РА и РВ. Для краткости говорят: сумма двух векторов есть вектор, являющийся диагональю параллелограмма, построенного на слагаемых векторах.
Это правило сложения векторов называют правилом параллелограмма. Оно, однако, непригодно, когда слагаемые векторы лежат на одной прямой - такие векторы называются коллинеарными; в этом случае применяют правило середины.
Рассмотрим, например, случай, когда вектор PC складывается с самим собой, т. е. когда разыскивается сумма PC + PC (рис.4а). Прибегнем к правилу середины: а) середина отрезка СС, соединяющего концы слагаемых векторов, есть, очевидно, точка С; б) остается
Рис.4 о. Сумма двух равных векторов:
PC→ +PC→ = 2 PC→ = PQ→ .
построить точку Q, симметричную точке Р относительно точки С, - она будет концом отрезка PQ, серединой которого является точка С.
Таким образом, вектор PC → + PC → направлен одинаково с вектором PC и имеет длину вдвое
большую, чем длина вектора PC. Этот вектор - сумму двух одинаковых слагаемых - обозначают 2· PC →. Итак:
РС → +РС → = 2 ·РС →. (2)
Полезно запомнить (это нам понадобится в дальнейшем), что если точка Q симметрична точке Р относительно точки С, то
Р Q → =2 ·РС → .
Эту формулу записывают также и в следующем виде:
PC → = 1 /2 · PQ →. (3)
Возвратимся теперь к случаю, когда складываются два произвольных коллинеарных вектора (сонаправленных или противонаправленных). Применяя правило середины, придем к следующим результатам: при сложении двух сонаправленных векторов1 РА → и
РВ (рис.4 б) получается вектор PQ →, который имеет такое же направление, как и слагаемые векторы, а его длина равна сумме длин слага-
¹ Т. е. таких, что точки P, A, B так расположены на одной прямой, что точка P лежит вне отрезка AB.
398
Рис.4 б. Сложение коллинеарных сонаправленных векторов: Р A → + PB → = PQ→ .
Рис.4 в. Сложение коллинеарных противонаправленных векторов: PA → +РВ → = PQ → .
емых векторов; при сложении двух противонаправленных векторов1 РА→ и РВ→ (рис.4в) получается вектор, имеющий направление такое же, как и направление того слагаемого вектора, который имеет большую длину; его длина равна разности длин слагаемых векторов.
Рассмотренное нами правило сложения векторов находит свое применение не только в математике, но играет очень важную роль также и в физике. Если в какой-либо точке Р приложены две силы, то, как известно, их совместное действие равносильно действию некоторой одной силы (также приложенной в точке Р) - ее называют равнодействующей. Многочисленные физические опыты и явления подтверждают справедливость следующего закона: если в точке Р приложены две силы, которые изображаются векторами РА→ и РВ→, то равнодействующая этих сил изображается вектором PQ→, который равен сумме векторов РА→ и РВ→.
Рис.5. Сложение двух равнопротивоположных векторов: РА → +РА → '= PP → .
Особое внимание следует уделить сложению векторов в случае, который изображен на рис.5. Здесь точка Р - общее начало обоих
¹ Векторов, у которых точка Р внутри отрезка АВ.
слагаемых векторов РА→ и РА→ ' - расположена в середине отрезка АА', соединяющего их концы. Такие векторы называются взаимно противоположными (или равнопротивоположными); они противонаправлены и имеют одну и ту же длину.
Применим к ним правило середины: а) строим середину С отрезка АА',- она совпадает, очевидно, с точкой Р; б) строим точку Q, симметричную точке Р относительно точки С, т. е. в данном случае относительно точки Р; получаем, что и точка Q совпадает с Р.
Таким образом, сумма двух равнопротивоположных векторов РА→ и РА→ ' есть вектор РР→ :
т. е. вектор, у которого конец совпадает с началом. Быть может, первое чувство побудит читателя отнестись с недоверием к такому вектору хотя бы потому, что у него нет направления. Но если отказаться от рассмотрения такого «особого» вектора, то придется признать, что не всякие два вектора можно сложить, а это, конечно, нежелательно.
Итак, любые две точки Р и А, независимо от того, различны они или совпадают,
определяют вектор РА→ .
Чтобы окончательно увериться в полезной роли «особого» вектора, убедимся, что
pa→ +pp→ =ра→ (5)
(это легко следует из правила середины).
Формула (5) показывает, что вектор РР→ играет в арифметике векторов такую же роль, какую число нуль играет в арифметике чисел. По этой
причине вектор РР→ называют нуль-вектором. Обратим еще внимание на то, что в формуле (4) вектор РА→ ' играет такую же роль, как и число -а в алгебраической формуле
а+(-а)= 0.
Целесообразно поэтому обозначать вектор РА→ ', равнопротивоположный вектору РА,
символом: - РА→ (словами - «минус РА→»).
Формула (4) может быть записана теперь в следующем виде:
РА→ +(-РА→)=РР→. (4')
Легко понять, что
-(-РА→) = РА→ . (4")
399
Свойства операции сложения векторов
Совпадают ли они со свойствами операции сложения чисел?
Начнем проверку со свойства переместительности. Нетрудно убедиться, что
PA→ + Р B → = Р B → + РА→
(ведь середина отрезка АВ есть в то же время и середина отрезка ВА).
Теперь выясним, обладает ли операция сложения векторов свойством сочетательности, т. е. справедливо ли равенство
(РА→ +РВ→)+РС→ =РА→ +(РВ→ + PC →). (6)
Начнем с проверки на каком-либо примере (рис.6 а,б). Убедимся, что действия над векторами РА→, РВ→, PC→, указанные в правой части формулы (6), приводят к тому же вектору
PR, к которому приводят действия, указанные в левой части равенства (6).
Посоветуем выполнить проверку справедливости формулы (6) и для других каких-либо
векторов РА'→, PB'→, PC'→ .
Можем ли мы теперь считать установленной справедливость формулы (6)?
Проверка справедливости сочетательного свойства сложения векторов даже на большом числе примеров не создает, конечно, полной
уверенности в справедливости этого свойства. Необходимо поэтому дать строгое доказательство. Используем для этого одну простую геометрическую теорему: если А', В', С', D' - середины сторон АВ, ВС, CD, DA произвольного
четырехугольника (даже и не выпуклого), то середина отрезка А'С' совпадет с серединой отрезки B'D' (т. е. четырехугольник A'B'C'D' есть параллелограмм).
Доказательство этой теоремы читатель легко проведет, если воспользуется известной теоремой о средней линии треугольника. Следует только терпеливо рассмотреть различные возможные случаи расположения исходных четырех произвольных точек А, В, С, D ; два из них показаны на рис, 7 а и 7 б.
Обратимся теперь к доказательству формулы (6). Возьмем три вектора РА, РВ, PC (рис.8 а), построим точки A ', В', С', симметричные точке Р относительно точек А, В, С соответственно, и обозначим буквами М и N середины сторон А'В' и В'С' четырехугольника РА'В'С'.
Примем теперь во внимание, что середина отрезка АВ совпадает с серединой отрезка РМ; это справедливо в силу упомянутой выше вспомогательной теоремы, если применить ее к треугольнику РА'В' (второй частный случай; он показан на рис.7 б). Поэтому, согласно правилу середины,
РА→ +РВ→ = РМ→ .
400
Пусть R - середина отрезка МС, a R' - точка, симметричная точке Р относительно точки R. Тогда
где S' - точка, симметричная точке Р относительно середины S отрезка AN.
Примем, наконец, во внимание, что точки R и S совпадают - это справедливо в силу указанной выше вспомогательной теоремы, если применить ее к четырехугольнику РА'В'С' ; отсюда PR' совпадает с PS', и, следовательно,
что и требовалось доказать.
Что такое сумма трех векторов? Ответ как будто очень простой - достаточно сложить два из них и полученный сложить с третьим. Но тут возникает вопрос: какие же два вектора из заданных трех сложить в первую очередь?
Однако теперь, когда мы убедились в справедливости переместительного и сочетательного свойств сложения векторов, можно установить понятие суммы трех векторов РА → , РВ → , PC →, не заботясь о том, какое из этих трех слагаемых считать первым, какое вторым, какое третьим.
В самом деле, все 6 возможных случаев (они указаны на таблице) дадут в результате
не 6 различных векторов, а один и тот же вектор PS → - это легко следует из доказанных нами двух свойств операции векторного сложения. Теперь уже нетрудно понять, как составить
сумму и четырех векторов РА → , РВ → , PC → , PD → (не беспокоясь опять о том, в каком порядке они заданы). Выберем какие-либо три из этих
векторов (скажем, PC → , PA → , PD →) и составим их
сумму: PC → + РА → + PD →. Прибавив к ней оставшееся четвертое слагаемое, получим вектор:
(PC → +РА → +PD →) + Р B → = Р S1 → .
Если бы мы начали со сложения других трех слагаемых, то получили бы еще три возможных вектора:
Какой из этих четырех векторов PS →1 следует назвать суммой наших четырех слагаемых?
На этот вопрос трудно (и даже невозможно!) было бы ответить, если бы операция сложения
401
двух векторов не обладала свойствами переместительности и сочетательности. Но, к счастью, эти свойства имеют место, а из них логически следует, что все четыре вектора PS → i равны между собой. Так, например:
Правые части этих формул равны между собой, и, следовательно,
Легко теперь понять, что результат сложения пяти слагаемых (шести, семи и т. д.) также не зависит от порядка, в котором они будут складываться. Можно также убедиться в справедливости сочетательного свойства суммы многих слагаемых, т е. доказать, что при нахождении суммы любого числа слагаемых векторов можно их произвольным образом сочетать в две группы: в первую войдут какие-либо из слагаемых, во вторую - все остальные. Если теперь составить сумму всех слагаемых, входящих в первую группу, и прибавить к ней сумму всех слагаемых, входящих во вторую группу, то получится вектор, равный сумме всех исходных векторов.
В дальнейшем мы познакомим читателя еще и с другими действиями над векторами: вычитанием вектора и умножением вектора и числа. Основные свойства этих операций мы запишем в общей, буквенной форме и таким образом ознакомимся с основами векторной алгебры.
Затем, что она создает возможность решать такие задачи геометрии, механики и физики, в которых в явной форме (а иной раз и в скрытой) участвуют направленные отрезки.
Мы уже говорили о том, что силы, рассматриваемые в механике и физике, очень наглядно изображаются векторами; такую же наглядность имеет векторное изображение перемещений, скоростей.
Не столь ясно, однако, на первый взгляд, какую роль могут сыграть векторы при изучении геометрии; но именно в этой области векторная алгебра с особенным успехом может быть использована для решения задач.
Суть дела коренится в следующем обстоятельстве. Изучение многих геометрических проблем сводится к изучению взаимного расположения отдельных точек пространства, составляющих рассматриваемые в задаче фигуры. Целесообразно поэтому выбрать в пространстве какую-либо одну определенную точку (обозначим ее буквой Р и будем называть начальной точкой или коротко - началом) и соединить ее направленным отрезком с каждой из тех точек А, В, С, которые входят в изучаемую фигуру.
Таким образом, мы получим векторы:
P А → , PB → , PC →,.. .,
т. е. для каждой точки М фигуры свой вектор: PМ →. Его называют радиус-вектором 1 точки М, и он полностью характеризует расположение точки М относительно начала. Другими словами, если точка М будет почему-либо утеряна, но сохранится ее радиус-вектор, мы ее легко восстановим, придется только учесть, где расположен конец этого радиус-вектора.
Эта формула очень легко получается - стоит только алгебраически записать правило середины, используя формулу (2). Если точка С - середина отрезка АВ, то по правилу середины:
PA → +PB → =PQ →,
где точка Q симметрична Р относительно точки С. Учитывая, что в силу формулы (2)
Р Q → = 2 · P С →,
1 Это название, введенное впервые Кеплером, удержалось до настоящего времени, хотя оно не совсем удачно; приставка «радиус» перед словом «вектор» может создать у читателя ложное представление, что вместе с радиус-вектором следует еще рассмотреть и некоторую окружность. Однако это не так; дело только в том, что существует единый центр Р (мы его назвали началом), в котором начинаются все радиус-векторы РА, РВ,... тех точек, которые мы изучаем.
402
получим важнейшее для геометрических приложений основное правило:
РА → +РВ → = 2 ·РС →. (8)
Очень полезно запомнить его словесную формулировку: сумма радиус-векторов двух каких-либо точек равна удвоенному радиус-вектору середины отрезка, определяемого этими точками. Эту формулу можно, очевидно (см. формулу (3), записать и в следующем виде:
РС → ( 1/2 )· (PA → +PB →), (8')
или словами: радиус-вектор середины отрезка равен половине суммы радиус-векторов концов этого отрезка.
Формулы (8) и (8') записывают, таким образом (на алгебраическом языке), простой геометрический факт - взаимное расположение середины произвольного отрезка относительно его концов. Это обстоятельство имеет очень важные последствия - оно создает возможность алгебраически записывать (как мы в этом скоро убедимся) и более сложные геометрические факты; отсюда возникает алгебраический (точнее, векторно-алгебраический) способ решения многих геометрических задач.
Этот метод изучения геометрии дает не меньше пользы, чем метод алгебраического решения арифметических задач. Покажем это на примерах.
Пусть точки A, B, C, D - последовательные вершины параллелограмма; А', В', С', D' - последовательные вершины другого параллелограмма. Обозначим точки, являющиеся серединами отрезков АА', B В', СС', DD', соответственно буквами А", B ", С", D" .
Что можно сказать о четырехугольнике А"В"С" D"? Посоветуем прежде всего сделать аккуратный чертеж, соответствующий условию задачи, он сразу подскажет ответ: четырехугольник A"B"C"D" - параллелограмм, у которого точки А", С" и В", D" - противоположные вершины.
Теперь следует дать геометрическое доказательство нашего (подсказанного только что проделанным опытом) предположения - пусть это сделает читатель самостоятельно. А сейчас познакомимся с новым - алгебраическим - методом решения этой задачи.
Начнем с того, что запишем, как это всегда делают при алгебраическом методе решения,
условие задачи с помощью формул. С этой целью выберем прежде всего какую-либо точку в качестве начала всех радиус-векторов тех 8 точек, которые заданы в условии задачи:
PA → , PB → , PC → , PD → ; PA' → , РВ' → , РС' → , PD' → .
Изобразите их на вашем чертеже.
Обозначим буквой М середину диагонали А С первого параллелограмма. Тогда, в силу формулы (8):
РА → +РС → = 2 ·РМ →. (a)
Примем теперь во внимание, что эта точка М является также и серединой диагонали BD; поэтому
PB → +PD → = 2 · PM →. (a ')
Из равенств (а) и (а') следует, что
РА → +РС → = PB → +PD →. (9)
Словами: если А, В, С, D - последовательные вершины какого-либо параллелограмма, то их радиус-векторы (относительно произвольно выбранного начала) удовлетворяют равенству (9).
Легко убедиться в справедливости и обратной теоремы: если радиус-векторы точек А, В, С, D (не лежащих на одной прямой) удовлетворяют равенству (9), то эти точки являются последовательными вершинами параллелограмма .
В самом деле, пусть М - середина отрезка АС, N - середина отрезка BD. Тогда, в силу основного правила (8), получим:
PA → + РС → = 2· PM → ; РВ → + PD → = 2 · PN →
По условию теоремы
РА → + РС → =РВ → + PD →, (a)
поэтому
2 · PM → = 2 · PN →, и, следовательно,
РМ → =PN →,
а это показывает, что точки М и N совпадают; таким образом, диагонали АС и BD четырехугольника ABCD делят друг друга пополам, а это означает, что ABCD - параллелограмм, что и требовалось доказать.
403
Равенство (9) записывает, таким образом, первую треть условия задачи; другая треть запишется, очевидно, равенством:
P А' → + РС' → = PB' → +PD' →. (9')
Перейдем теперь к алгебраической записи требований, содержащихся в доказываемой нами теореме; они, очевидно, состоят в том, что нужно доказать справедливость равенства:
P А" → + РС'' → = P В" → + PD" → (10)
(потому что его справедливость есть, как мы это выше установили, условие того, что точки А", В", С", D" - вершины параллелограмма). Приступая к доказательству справедливости формулы (10), примем сначала во внимание, что по условию задачи (еще не записанная оставшаяся треть условия!)
2· РА → =РА → + РА' → ; 2· PC" → = PC → + PC '→ и, следовательно,
2· РА'' → + 2· PC "→ = P А → +PA' → +PC → + РС' → ; поэтому
2· (РА" → + PC '' →) = PA → +РА' → + РС → + PC '→. (b) Учтем еще, что по условию задачи
2· Р B "→ = РВ → + P В' → ; 2 · PD " → =PD → + PD' →, и получим:
2· (PB "→ + 2 PD ''→) = P В → + PB' → + PD → + PD' →. (b ')
Нетрудно, однако, убедиться в том, что правые части равенств (b) и (b ') равны между собой - это сразу следует из формул (9) и (9'), с помощью которых мы записали условие задачи (если их почленно сложить и воспользоваться тем замечательным свойством сочетательности суммы многих векторов, о котором мы говорили на стр. 402). Отсюда следует, что и левые части формул (b) и (b ') равны между собой, т. е. что
2· (РА" → + PC "→) =2· (РВ" → + PD "→);
поэтому оказывается справедливым равенство, которое и требовалось доказать.
Оно возникает, если принять во внимание,
что радиусы-векторы РА → , РВ → , PC →, ... точек А, В, С, ..., рассматриваемых в какой-либо задаче, все имеют общее начало Р. Целесообразно поэтому не включать букву Р, изображающую это начало, в обозначение радиус-вектора, а сохранить в обозначении только его конец, т. е. точку, которую он изображает.
Таким образом, векторы РА, РВ, PC, ... будем обозначать А, В, С, .... Это упростит внешний вид формул. Чтобы привыкнуть к таким обозначениям, полезно вернуться к решению задачи о двух параллелограммах и записать ее решение в новых обозначениях.
Укажем еще, что в печатном тексте вместо изображения радиус-векторов символами A, B ,... используют А, В, ..., т. е. те же буквы, но набранные жирным шрифтом.
1. Произвольная точка Р отражена от середины сторон треугольника A1 A2 A3, т. е. построены точки:
P1 - симметричная точке Р относительно середины стороны А2 А3,
P2 - симметричная точке Р относительно середины стороны А3 А1,
P3 - симметричная точке Р относительно середины стороны А1 А2 .
Что можно сказать об отрезках А1 Р1 , А2 Р2 А3 Р3 ?
Ответ подскажет опыт, т. е. тщательно выполненный чертеж. Он покажет, что эти три отрезка пересекаются в одной точке, которая делит каждый из них пополам.
Рис.9 а. Первая задача о треугольнике.
Для доказательства выберем начало радиус-векторов в точке Р и, используя экономные обозначения, обозначим А1 , А2, А3 радиус-векторы вершин заданного треугольника (рис.9 а). (Не советуем эти радиус-
404
векторы проводить на чертеже, достаточно себе их представить.) Тогда, в силу условия задачи, радиус-векторы точек Р1, Р2, P3, отражений точки Р, определяются по формулам:
P1 = A2 ,+А3 ; Р2 =А3 +А1 ; Р 3 = А1 +А2 . Пусть С1 - середина отрезка A1 P1 ; тогда:
2 ·С1 =А1 +Р1 =А1 + (А2 +А3). Пусть С2 - середина отрезка А2 Р2, тогда:
2 · C2 =A2 +P2 =A2 +(A3 +А1).
Учитывая, что правые части этих формул равны между собой, придем к выводу, что 2· С 1 = 2· С 2, т. е. убедимся, что отрезки А1 Р1 и А2 Р2 имеют общую середину С, имеющую радиус-вектор C1 = С2. Аналогичным способом убедимся, что и отрезки A1 P1 и А3 Р3 имеют общую середину С, имеющую радиус-вектор C 1 = С 3, Таким образом, все три отрезка имеют общую середину С, а это и требовалось доказать. Запомним, что
2· C = A1 +A2 +A3 (a)
2. Пусть точки Ql, Q2, Q3 - середины отрезков Р2 Р3, P3 P1 ,,P1 P2, рассмотренных в предыдущей задаче, а точки М1, М2, М3 - середины сторон А2 А3, А3 А1 , А1 А2. Что можно сказать об отрезках M1 Q, M2 Q2 , M3 Q3 ?
Рис.9 б. Вторая задача о треугольнике.
Из рис.9 б видно, что они пересекаются в одной точке, которая является их общей серединой. Вот алгебраическое доказательство:
2· Q1 = Р2 +Р3 =(А3 +А1) + (А1 +А2)=2 ·А1 +А2 +А3, (b)
2· Q2 = P3 +Р1 = (А1 + A2) +(А2 +А3)= 2 · A2 +A3 +A1, (b ')
2 · Q3 =Р1 +Р2 = (А2 +А3) +(А3 +А1) = 2 · A3 +A1 +A2, (b '')
Если D1 - середина отрезка М1 Q1, то 2 · Dl = M1 +Q1
и, следовательно,
Аналогичным образом получим:
Правые части формул (g), (g '), (g ") равны между собой, и поэтому D1 = D2 = D3, что и требовалось доказать.
3. Что можно сказать о прямых A1 Q1, A2 Q2 , A3 Q3 ?
Ответ. Они пересекаются в одной точке, которая симметрична точке Р относительно точки С (сделать чертеж).
Доказательство. Обозначим буквой Р' точку, симметричную точке Р относительно точки С; тогда Р' =2 С и, в силу формулы (a),
P'=A1 +A2 +A3.
Обозначим теперь буквой А1 ' середину отрезка А1 Р '; тогда:
2·А'1 =А1 +Р'=2·А1 +А2 +А3. Правая часть этой формулы совпадает с правой частью формулы (b), и поэтому А'1 = Q1, т. е. точка А'1 есть не что иное, как уже известная нам точка Q1. Отсюда следует, что точка Р' лежит на прямой A1 Q1 .
Аналогичным образом докажем, что она лежит и на прямой A2 Q2, и на прямой A3 Q3, а это и требовалось доказать.
Шестиугольник А1 А2 А3 А4 А5 А6 будем называть центральным, если его главные диагонали А1 А4 , А2 А5 , А3 А6 пересекаются в одной точке и делятся в этой точке пополам. Эту точку будем называть центром центрального шестиугольника 1 .
1 Если вершины шестиугольника лежат в одной плоскости, то он называется плоским, если же они не лежат в одной плоскости, то он называется косым. Центральный шестиугольник может быть либо плоским, либо косым. Но центральный четырехугольник обязательно плоский - это просто параллелограмм.
405
Рассмотрим теперь вместе с центральным шестиугольником A1 A2 A3 A4 A5 A6 еще и какой-либо другой центральный шестиугольник Bl B2 B3 B4 B5 B6 и рассмотрим точки C1 , C2, С3, С4, С5 , С6, являющиеся серединами отрезков А1 B1 , A2 B2, ..., А6 B6 .
Требуется доказать, что эти точки являются последовательными вершинами центрального шестиугольника и что его центр делит пополам отрезок, соединяющий центры обоих исходных шестиугольников.
Для доказательства полезно прежде всего доказать: если точки P1,..., Р6 последовательные вершины центрального шестиугольника, то радиус-векторы P 1,..., P 6 его вершин удовлетворяют следующим двум равенствам:
Р1 + Р4 = Р2 + Р5 ; Р2 + Р5 = Р3 +Р6 (a)
и наоборот.
Далее нужно записать в алгебраической форме условие задачи (это приведет к четырем векторным равенствам), учесть, что радиус-векторы точек Ci определяются формулой:
Ci = 1/2 (Ai +Bi) (i = l, 2,...,6),
и убедиться, что из упомянутых четырех условий следует, что векторы Сi удовлетворяют соотношениям (а).
По заданным трем точкам А, В, С построим: а) середину С' отрезка АВ, а затем середину С" отрезка СС';
б) середину А' отрезка ВС, а затем середину А" отрезка АА'.
Возможно ли такое расположение исходных трех точек А, В, С, при котором точка А" совпадает с точкой С"?
Ответ. Только в том случае, когда точки А и С совпадают.
Решение.
2 · С '= А + В ,
2 · С " = С "+ С, и поэтому
2 · (2 С'')=(С '+ С) + (С '+ С) = 2 · С '+ 2 · С ; таким образом,
2 ·( 2 · С ")=(А + В)+ 2 · С =(А + В + С)+ С . (a)
Аналогично получим:
2 ·( 2 · А ")=(В + С + А)+ А . (a ')
Точки С" и А" совпадут, если С "= А ", т. е. в силу формул (a) и (a '), если
(А + В + С)+ С = (В + С + А)+ А ;
а это равенство возможно только при С = А, т. е. если точка А совпадает с точкой С.
1. Условимся в следующих обозначениях:
РА → = 1· PA → ; РА → +РА → = 2 ·РА → PA → + РА → + РА → = 3 ·РА →,
А'+А+А+А=4·А и т. д. (a)
Доказать, что для произвольных целых чисел m и n справедливы равенства:
m · А + n · А =(m + n) · А ; (b1)
m · (А + В)= m ·А + m ·В ; (b2)
n · (m · А)=(n · m) · А. (b3)
Справедливость формул (b) делает целесообразным называть вектор m · А произведением числа т к вектора А. Таким образом, эта операция обладает свойством распределительности (формулы b1 и b2) и сочетательности (формула b3).
2. Пусть С - середина отрезка АВ, С' - середина отрезка АС и С" - середина отрезка С'В.
Выразить радиус-векторы точек С' и С" через радиус-векторы точек А и В.
Ответ. 4 · С' = 3. А + В ; 4 · С "= А +3· В .
3. Средним отрезком произвольного четырехугольника (даже и не плоского) называют отрезок, соединяющий середины его двух противоположных сторон. Доказать, что средние отрезки четырехугольника пересекаются и делят друг друга пополам.
Указание к решению. Если А, В, C,D - последовательные вершины четырехугольника и если точка М - середина среднего отрезка, соединяющего середину стороны АВ с серединой стороны CD, то 4· М =(А + В) + (С + D).
Точку пересечения обоих средних отрезков называют центроидом четырехугольника ABCD.
4. Каждая треугольная пирамида ABCD имеет три пары противоположных ребер: АВ и CD ; АС и BD ; AD и ВС. Средним отрезком
406
пирамиды называют отрезок, соединяющий середины какой-либо пары противоположных ребер.
Доказать, что все три средних отрезка пирамиды пересекаются в одной точке и делятся в ней пополам. Эту точку называют центроидом пирамиды.
5. Доказать, что если S1, S2, S3 , S4 - середины сторон А1 А2 , А2 А3 , А3 А4 , А4 А1 произвольного (даже и не плоского) четырехугольника, то они являются последовательными вершинами параллелограмма
6. Для произвольного восьмиугольника А1 А2 ...А8 построены центроиды1 S1, S2, ..., S8 четырехугольников: А1 А2 А3 А4 , А2 А3 А4 А5 , ..., A5 A6 A7 A8 , A6 A7 A8 A1, ..., А8 А1 А2 А3 .
Доказать, что восьмиугольник S1 S2 ...S8 - центральный, т. е. что его диаметры S1S5, S2 S6, S3 S7 , S4 S8 пересекаются в общей точке, которая делит каждый из них пополам.
7. Пусть точки B1 , B2, ...,В6 - середины сторон А1 А2, A2 A3 , ..., А5 А6, А6 А1 центрального шестиугольника. Доказать, что они также являются последовательными вершинами центрального шестиугольника.
Каково взаимное расположение центров обоих шестиугольников? Ответ. Они совпадают.
8. По двум заданным центральным шестиугольникам А1 А2 ...А6 и B1 B2 ...B6 построить шестиугольник C1 C2 ...C6 такой, что его вершина Сi симметрична вершине Аi, относительно середины отрезка Bi Bi +1 (i = 1, 2, ..., 6;
B7 = B1).
Что можно сказать о многоугольнике
C1 C2 ...C6 ?
Ответ. Он центральный; его центр симметричен центру многоугольника А1, ...А6 относительно центра многоугольника В1 ...В6 .
9. Сформулировать и решить задачу для двух центральных восьмиугольников, аналогичную предыдущей задаче.
10. Доказать, что
-(A + В) = (- А)+(- В). Указание. Используя сочетательное свойство сложения и формулы (4') и (4"), убедиться в справедливости равенства:
(А + В)+ {(- А ) + (- В)}= PP → .
11. Найти вектор X, удовлетворяющий уравнению:
Х + А = В .
Доказать, что это решение единственное.
Ответ. X = В +(- А).
Замечание. Вектор В +(- А) называют разностью векторов; B (уменьшаемый вектор) л А (вычитаемый).
В векторной алгебре его принято обозначать: В - А . Поэтому в последующих задачах используется равенство:
В - А = В +(- А).
12. Доказать, что
(А + В)- С = А +(В - С).
Каждый из этих векторов принято записывать:
А + В - С.
13. Доказать, что
А -(В + С)=(А - В)- С . (Принята запись: (А - В) - С = А - В - С .)
14. Доказать, что
А - (В - С) = (А - В) + С . (Принята запись: (А - В) + С = А - В + С .)
15. По заданным радиус-векторам точек А и С выразить (вычислить) радиус-вектор точки A', симметричной точке А относительно точки С. Ответ. А '= 2 · С-А .
16. Точка М отражается от вершины А1 произвольного треугольника A1 A2 A3, т. е. строится точка M1; симметричная точке М относительно точки А1. Полученная точка М1 отражается от вершины А2 ; получаем точку M2, которую отражаем от вершины А3 ; возникает точка М3 .
Что можно сказать о взаимном расположении точки М3 относительно исходной точки М ?
Ответ. Точка М3 симметрична точке М относительно точки A4, которая является четвертой вершиной параллелограмма, построенного на векторах А2 А1 → и А2 А3 → .
17. На отрезке MN расположены точки M1 и М2 так, что M1 есть середина отрезка MM2, а М2 - середина отрезка M1 N . Выразить радиус-векторы точек М1 и M2 через радиус-векторы точек М и N.
Ответ. М 1 =1 /3 · (2 · М + N);
О
М 2 = 1/3 ·(М + 2 · N).
18. Разделим какую-либо медиану треугольника А B С на три равных отрезка и рассмотрим ту точку деления S, которая ближе к основанию.
Выразить радиусы-векторы точки S через радиус-векторы точек А, В, С.
¹ См. задачу 3.
407
Указание. Конец А' медианы АА'
имеет радиус-вектор 1/2 (В + С); далее использовать результат предыдущей задачи.
Ответ. S =1 /3 · (А + В + С);
он показывает, что точка S лежит и на медиане ВВ', и на медиане СС' (таким образом, получено векторное доказательство известной теоремы о трех медианах). Точку S называют центроидом треугольника.
19. Для заданного произвольного шестиугольника А1 А2 А3 А4 А5 А6 построим центроиды S1, S2, S3 , S4, S5 , S6 треугольников A1 A2 A3, А2 А3 А4 , ..., А5 А6 А1 , А6 А1 А2 .
Доказать, что точки Si - последовательные вершины центрального шестиугольника.
Вообразим, что нам удалось собрать математиков разных веков и стран и поставить перед ними вопрос: «Что вы можете сказать о формуле квадрата суммы?» Стенограмма этой необычной конференции могла бы выглядеть примерно так.
Вавилонский математик, живший 4000 лет назад, сказал, что никаких формул он не знает, так как считает не буквами, а числами. Но ему известно, что если взять два числа, например 20 и 3, то для вычисления квадрата их суммы надо возвести в квадрат число 20, потом число 3, сложить эти квадраты и к сумме прибавить удвоенное произведение чисел. Это же правило годится и для любых других двух чисел.
Древний грек, живший 2300 лет назад, доказал это правило. Он нарисовал чертеж (рис.1) и сказал, что площадь квадрата А С (т. е. квадрата, у которого точки А ж С являются концами диагонали) равна сумме площадей квадратов АВ и ВС и удвоенной площади прямоугольника BD. Поэтому, если сторона квадрата АВ равна 20, а квадрата ВС равна 3, то площадь квадрата АС действительно можно
408
подсчитать так, как предложил его вавилонский коллега.
Алгебраист XVI в. записал формулу квадрата суммы в следующем виде:
В переводе это читалось бы примерно так: А + В в квадрате равно А в квадрате + В в квадрате + А на В2. (Как видите, вместо скобок он писал черту, степени обозначал словами, а коэффициенты писал в конце.)
- Не слишком удобные обозначения,- сказал иронически математик XVII в.
- Однако и с этими обозначениями мы умеем делать значительно больше, чем древние греки,- с обидой возразил выступавший.- Они умели решать лишь квадратные уравнения, а мы справляемся и с уравнениями третьей и четвертой степеней. Жаль лишь, что слишком часто эти уравнения не решаются, так как полученные формулы приводят к нелепой операции извлечения квадратного корня из отрицательного числа.
Выступавший следующим алгебраист XVII в. написал формулу квадрата суммы уже в привычном для нас виде:
(а + b)² =а² +2 а b + b² .
Он добавил, что его предшественники слишком узко понимают эту формулу. Прежде всего, в ней а и b не обязательно являются длинами отрезков, а сами могут быть площадями, объемами, весами и даже отрицательными числами. Более того, вместо а и b в эту формулу можно подставить любые многочлены, например:
[ x² + (х +1)]² = x 4 +2 х² (х+ 1) + (х+ 1)² .
Он сказал еще, что эта формула является только одной из большого числа знакомых ему алгебраических формул и что ему хорошо известно искусство буквенных вычислений, а это искусство и есть алгебра.
Алгебраист XVIII в. заявил, что о формуле квадрата суммы нечего много говорить: эта формула, как и все буквенные вычисления,- удел школьной математики. При этом он отметил, что она всегда верна, и притом не только для положительных или отрицательных чисел, но и для комплексных, а эти числа совсем не такая уж нелепость! Что же касается предмета алгебраической науки, то это вовсе не искусство буквенных вычислений, а умение решать уравнения и системы уравнений. Для систем уравнений первой степени у него даже есть общая формула решения.
Выступление математика XIX в. часто прерывалось возгласами недоверия и шумными восклицаниями. Было ясно, что это выступление явилось для большинства участников полной неожиданностью. Да и в самом деле, выступавший заявил, что формула (а + b)² = а² +2 а b + b² верна далеко не во всех случаях! Например, английский математик У. Гамильтон занимался обобщением комплексных чисел. Он построил числа, названные кватернионами, у которых не одна, а целые три мнимые единицы i, j, k. Так вот, для кватернионов (которые находят много интересных применений) формула квадрата суммы просто неверна. Неверна потому, что здесь мы сталкиваемся со случаем, когда умножение некоммутативное, т. е. не выполняется переместительиый закон умножения (например, ij = k, ji =- k), а при выводе формулы квадрата суммы мы пользуемся равенством ab = b а.
Выступавший сказал, что другие математики рассмотрели еще более удивительные обобщения комплексных чисел, для которых умножение не только некоммутативно, но даже и неассоциативно, т. е. в общем случае
(а b) ¹ (b с).
Выступивший вслед затем алгебраист XX в. сказал, что гиперкомплексные числа - это только примеры к тем общим теориям, которыми он занимается. Он может доказывать теоремы, которые верны не только для гиперкомплексных чисел одного вида, а для всех гиперкомплексных чисел (или для очень многих видов таких чисел). Он умеет складывать и умножать не только числа и многочлены, а и такие вещи, как квадратные таблицы, геометрические и алгебраические преобразования, логические суждения и т. д. (см. статью «Алгебра множеств и алгебра логики»).
409
- Как же вам удается оперировать с такими непохожими друг на друга вещами, как квадратные таблицы, гиперкомплексные числа, геометрические преобразования? Что может быть общего в действиях над ними? И как вы узнаете, какие формулы имеют место в тех или иных случаях?
- Весьма несложно; для этого в моем распоряжении имеется столь мощное оружие, как аксиоматический метод, который...
- Не может быть,- воскликнул окончательно выведенный из равновесия древний грек,- ведь аксиомы относятся к области геометрии?!
...Прервем на этом нашу конференцию и постараемся разобраться во всем сказанном.
Из всех сделанных высказываний школьнику Васе Игнатьеву, который был корреспондентом школьной стенгазеты и присутствовал на конференции, самым правильным показалось мнение алгебраиста XVII в., что алгебра - искусство буквенных вычислений. Вася учился тогда в седьмом классе и на уроках алгебры много занимался буквенными вычислениями. Тут были и формулы сокращенного умножения, и коэффициенты, и показатели степени, и многое другое - от букв в глазах рябило. Он часто думал: «Хорошо было бы иметь ответы ко всем примерам из Ларичева!» Но вскоре понял, что это не поможет,- учитель для контрольных работ брал примеры из какого-то другого задачника. А запомнить решения всех
задач из всех задачников на свете - это, пожалуй, никому не под силу, разве что фокусникам из цирка, выступающим с сеансами феноменальной памяти.
Делать нечего, приходилось заучивать правила: что происходит с коэффициентами и показателями при умножении одночленов, как возводить сумму и разность в квадрат и многое другое.
Вася был мальчик любознательный и захотел узнать, откуда же эти правила берутся. Внимательно читая учебник, он понял, что все правила, по которым выполняются действия с многочленами, вытекают из небольшого числа основных правил. Эти первоначальные правила таковы:
Из этих правил можно вывести все остальные. Покажем, как выводится формула
(а + b)² = а² +2 а b + b², (2)
обсуждавшаяся на необычной конференции. По закону дистрибутивности имеем:
(а+ b)² =(а+ b)(а+ b) =(а + b)а +(а+ b)b.
Используя коммутативность умножения, получаем:
(а+ b)² = а (а+ b) + b (а+ b).
Вторично применяя дистрибутивность, а также коммутативность умножения и ассоциативность сложения, находим: (a + b)² =(а² + а b)+(b а+ b²) =(а² + ab)+ (а b + b²)= а² + (а b + ab) + b². Здесь
а b +а b = а b · 1+ ab · 1= а b (1+1)= а b · 2=2 а b, и потому
(а+ b)² =а² +2 а b + b². Попробуйте таким же способом проследить вывод формулы:
(а+ b)³ = а³ +3 а² b +3 а b² + b³. Вы увидите, что при этом придется использовать и закон ассоциативности умножения.
410
Итак, правила алгебры выводятся из написанных нами первоначальных правил. Таким образом, искусство буквенных вычислений сводится к применению этих основных правил. При этом некоторые следствия из этих правил (например, формула квадрата суммы) применяются настолько часто, что их надо так же хорошо запомнить и применять, как и первоначальные правила.
Не правда ли, это очень напоминает положение дел в геометрии - там тоже есть несколько аксиом (т. е. первоначальных положений), из которых выводятся различные следствия, называемые теоремами. А при решении задач приходится применять и аксиомы, и теоремы. Поэтому мы будем, как и в геометрии, формулы (1) называть аксиомами, а формулы вида (2) - теоремами.
Как и аксиомы геометрии, аксиомы алгебры не доказываются. Они являются обобщением многотысячелетнего опыта практической деятельности человечества. Прежде чем сформулировать положение: a + b = b + а, надо было много тысяч раз подметить такие арифметические соотношения, как: 2 + 5 = 5 + 2, 4 + 6 = 6 + 4 и т. д.
Все остальные аксиомы (1) имеют такое же происхождение: они являются буквенной записью многократно проверявшихся законов арифметики.
Уже шестиклассники хорошо понимают, насколько алгебра сильнее арифметики: вместо того чтобы решать несколько задач, отличающихся только числовыми данными, можно решить одну задачу с буквенными данными, а потом подставлять в полученный ответ различные числовые данные. Достаточно напомнить задачу:
Смешали а кГ конфет ценой m рублей за 1 кГ и b кГ конфет ценой n рублей за 1 кГ. Сколько стоит 1 кГ полученной смеси?
Решение этой задачи дается буквенной формулой:
A=(ma+nb)/(a+b)
· где А - стоимость 1 кГ смеси.
При этом полученный алгебраический ответ часто можно упростить, пользуясь правилами алгебраических преобразований, и тогда подставлять числовые данные будет гораздо проще.
На этом факте основаны многочисленные «фокусы» с отгадыванием задуманных чисел.
Например, предложим выполнить следующие действия: 1) задумайте число; 2) прибавьте к задуманному числу 5; 3) полученный результат умножьте на 3; 4) отнимите от получившегося теперь результата задуманное число; 5) отнимите 11; 6) разделите полученный ответ на 2. Если сообщить «фокуснику» полученный результат, то он сразу назовет задуманное число. При этом ему не придется выполнять в обратном порядке всей сложной последовательности действий. В самом деле, если обозначить задуманное число через х, то действия, которые предложено выполнить, записываются следующим образом:
[(х +5)·3- x -11]:2.
Упрощая это выражение, легко найдем, что оно равно х +2. Поэтому «фокуснику» достаточно отнять от сообщенного ему результата 2, чтобы получить задуманное число.
Однако шестиклассник (да и оканчивающий школу) не оценивает полностью всю силу буквенных формул. Он считает, что буквы в них - это обязательно какие-то числа (заранее известные или искомые). На самом же деле, производя действия с буквами, он использует лишь аксиомы алгебры и их следствия. Поэтому все его вычисления годятся не только для чисел, но и для любых вещей, для которых выполняются эти аксиомы. Например, буквы могут означать не отдельные числа, а многочлены, алгебраические дроби и другие алгебраические выражения.
Ведь хорошо известно, что для сложения и умножения многочленов выполняются те же аксиомы (1), что и для сложения и умножения чисел. Например, если а и b - некоторые многочлены, то а + b = b +а, а b = b а и т. д. Отсюда следует, что в любое алгебраическое тождество вместо букв можно подставлять не только числа, но и любые многочлены. Например, из того, что
a³ - b³ =(a - b)(a² + ab + b²),
следует тождество:
(x² + х +1)³ -(x² - х +1)³ = 2 х[(х² + х +1)² + (х² + х +1 )(x² - х +1)+ (x² - x +1)²]].
Если, кроме чисел и многочленов, нам встретятся другие вещи, которые можно складывать и умножать, причем выполняются аксиомы (1), то для них будут верны все формулы и выводы алгебры.
411
Например, старшеклассники встречаются с комплексными числами. Верны ли для таких чисел формулы алгебры, или надо снова выяснять, чему равен куб суммы комплексных чисел?
Из сказанного следует, что проверять заново для комплексных чисел все формулы алгебры не нужно. Достаточно проверить аксиомы (1), а из них уже будут следовать все остальные формулы.
Теперь ясно, когда верна формула
(а + b)² =а² + 2ab + b²,
да и все остальные формулы алгебры. Они верны для любых объектов, которые можно складывать и умножать, причем выполняются указанные выше аксиомы (1). Мы уже знаем три примера объектов, для которых эти аксиомы выполняются. Это - действительные числа, комплексные числа и многочлены.
Математики знают много других примеров множеств с аналогичными свойствами:
1) элементы такого множества можно складывать и умножать, причем сумма и произведение двух элементов снова принадлежат тому же множеству;
2) среди элементов множества особо отмечены два элемента, обозначаемые символами О и 1;
3) для каждого элемента а определен противоположный элемент -а, принадлежащий тому же множеству;
4) для сложения и умножения в рассматриваемом множестве выполняются все аксиомы (1).
Ввиду того что такие множества часто встречаются, для них было введено специальное название - кольцо.
Кроме рассмотренных выше трех примеров, можно указать следующие примеры колец: а) множество всех целых чисел (сумма и произведение целых чисел - целые числа, так же как и число, противоположное целому); б) многочлены с целыми коэффициентами; в) числа вида а + b √‾7, где а и b - произвольные целые числа.
А положительные числа (относительно обычных сложения и умножения) кольца не образуют, ведь число, противоположное положительному, уже не является положительным.
Позже понятие кольца было расширено. Во-первых, отказались от требования,
что в кольцо входит элемент 1, для которого a · 1= 1· a = а. Например, все четные числа (как положительные, так и отрицательные) образуют кольцо без единицы. Нечетные же числа вообще не образуют кольца, так как сумма двух нечетных чисел четна.
Потом отказались и от требования коммутативности умножения, т. е. отбросили аксиому а b = b а (сохранив остальные аксиомы). Такие кольца стали называть некоммутативными. Примером некоммутативного кольца является кольцо всех кватернионов. Наконец, пожертвовали и аксиомой ассоциативности умножения, заменив ее другими аксиомами.
Например, стали рассматривать кольца, в которых аксиомы коммутативности и ассоциативности умножения заменяются следующими аксиомами:
а b=-b а (антикоммутативность); (ab)c + (bc)a + (са) b = 0.
Такие кольца называют алгебрами Ли (по имени норвежского математика С. Ли).
Все это происходило не из любви математиков к обобщениям, а потому, что были найдены важные для практики объекты, для которых имелось естественное сложение и умножение, но умножение не было ни коммутативным, ни ассоциативным. Многие такие объекты встретились, например, в современной квантовой физике.
Разумеется, вследствие введения новых аксиом пришлось заменить многие формулы алгебры новыми. Например, для алгебр Ли вместо формулы (а- b)(а + b)=а² - b² справедлива формула (а - b)(а + b)= 2 ab. Не правда ли, удивительно?!
Мы уже говорили, что понятие кольца, удовлетворяющего всем аксиомам (1), оказалось в некоторых вопросах математики слишком узким. Однако для других математических вопросов оно оказалось слишком широким, ведь в определении кольца ни звука не сказано о возможности деления. Да и не во всех кольцах можно делить. Возьмем, например, кольцо всех (положительных и отрицательных) целых чисел. Если разделить 3 на 5, то целого числа не получится. А без деления нельзя решать даже уравнений первой степени!
412
Чтобы изучать уравнения, пришлось ограничиться кольцами, в которых есть операция деления. Такие кольца математики назвали полями. Как в настоящем поле можно идти в любую сторону, не встречая никаких препятствий, так в математическом поле можно беспрепятственно выполнять все арифметические действия. Впрочем, одно ограничение есть - на нуль в поле делить нельзя.
Читатель еще в шестом классе познакомился с одним полем - полем всех рациональных чисел (положительных и отрицательных). Позже он познакомился с другим, более широким полем - всех действительных чисел (как рациональных, так и иррациональных). Наконец, все комплексные числа тоже образуют поле.
Кроме этих трех полей (рациональных, действительных, комплексных чисел), есть еще много других полей, состоящих из чисел. Возьмем, например, все числа вида а + b √‾3, где а и и b - рациональные числа. В это множество чисел входит, например, √‾3=0+1· √‾3, но не входит √‾5. Покажем, что это множество чисел образует поле.
В самом деле, возьмем два числа: а + b √‾3, с + d √‾3 из нашего множества. Их сумма имеет вид:
(а + b √‾3)+ (с+ d √‾3)= (а + с)+ (b + d) √‾3.
Так как а + с и b + d - рациональные числа, то число (а + b √‾3) +(c + d √‾3) также принадлежит нашему множеству. Точно так же из равенств:
(а+ b √‾3) (с+ d √‾3)= ас + ad √‾3 + b с √‾3+ 3bd = (ас+3 bd)+ (ad + bc) √‾3
следует, что произведение двух чисел рассматриваемого множества снова принадлежит ему. Сложнее обстоит дело с частным. Возьмем число (a + b √‾3)/(c + d √‾3). Чтобы записать его в виде m + n √‾3, освободимся и от иррациональности в знаменателе:
Числа (ac -3 bd)/ c² -3 d²) и (bc-ad)/(c² -3 d²) рациональны, а потому (a+b √‾3)/(c+d √‾3) принадлежит нашему множеству.
Впрочем, не спешите, не все числа можно делить друг на друга (даже в поле рациональных чисел). Если число с² -3 d² окажется равным нулю, то у нас ничего не получится. Но при рациональных с т d равенство с² - 3d² = 0 может иметь место только в том случае, если с = d = 0. А в этом случае число с + d √‾3 равно нулю и делить на него нельзя.
Докажите сами, что числа а + b √‾5, где а и b - рациональны, образуют поле. А вот числа вида а + b √‾2 + с √‾3, где а, b, с - рациональны, не образуют поля, потому что √‾2 · √‾3 = √‾6. Чтобы получить поле, надо расширить это множество чисел, а именно рассматривать числа вида а + b √‾2+ c √‾3 + d √‾6, где а, b, с, d - рациональны. Поля можно строить не только из чисел. Например, множество всех алгебраических дробей образует поле.
С разложением чисел на множители учащиеся знакомятся еще в начальной школе. При отыскании общего знаменателя им приходится разлагать на множители знаменатели слагаемых. Нужно разложение на множители и при сокращении дробей.
Одно из основных утверждений арифметики гласит: каждое натуральное число единственным образом разлагается на простые множители. Например:
72 = 2·2·2·3·3; 1001=7·11·13
(разумеется, разложения, отличающиеся лишь порядком множителей, мы считаем одинаковыми). Напомним, что простым числом называется натуральное число, имеющее только два различных делителя (само число и 1). Число 1 не считается простым.
Будем теперь рассматривать не только натуральные числа, но и нуль, и отрицательные целые числа. Иными словами, возьмем множество всех целых чисел. На первый взгляд здесь труднее определить понятие простого числа. Ведь, например, 7 = (-1)·(-7). Значит ли это, что число 7 перестает быть простым, если его
413
рассматривать в множестве всех целых чисел? Оказывается, нет, надо только уточнить, что называется простым числом.
Заметим, что число -1 обладает следующим свойством: если разделить 1 на -1, то в частном получится целое число. Другим целым числом с таким же свойством является сама единица. Мы будем называть эти числа (1 и -1) делителями единицы.
Назовем целое число р простым, если оно не является делителем единицы, но в любом его разложении в произведение двух целых множителей один из сомножителей обязательно является делителем единицы. При таком определении число 7 остается простым и после перехода к множеству всех целых чисел. Простым будет и число -7.
Сохраняет свою силу и основной закон арифметики, однако тоже с небольшим изменением формулировки: каждое целое число, отличное от нуля, разлагается в произведение простых целых чисел ; это разложение однозначно определено с точностью до перестановок сомножителей и возможного умножения некоторых сомножителей на - 1 (т. е. на делитель единицы). Например,
21 = 3·7=7·3= (-3)(-7)=(-7)(-3). Такие разложения принято считать неотличающимися друг от друга.
При решении некоторых сложных вопросов теории чисел пришлось разлагать целые числа не только на целые множители, но и на множители вида а + b √‾5, где а и b - целые числа. Числа такого вида сами образуют кольцо. Для них, как и для целых чисел, можно определить понятия простого числа, делителя единицы и т. д. Например, число 2+ √‾5 - делитель единицы, так как(2+ √‾5)(-2+ √‾5)=1. Велико же было удивление математиков, когда оказалось, что в кольце чисел а + b √‾5 нарушается основной закон арифметики о единственности разложения на простые множители. Например,
Не однозначно разложение на простые множители и в кольце чисел вида а + b √‾- 5, где
а и b - целые. В этом кольце единственными делителями единицы являются те же числа 1 и -1, что и в кольце целых чисел. Однако
21=3·7=(4+ √‾-5)(4- √‾- 5)=(1-2 √‾-5)(1+2 √‾-5).
А вот в кольце чисел вида a+b √‾3 (а и b -целые) имеются делители единицы, кроме 1 и -1, например: (2+ √‾3)(2- √‾3)=1. Но разложение на множители в этом кольце однозначно (как всегда, с точностью до перестановки множителей и умножения этих множителей на делители единицы).
В теории чисел полностью изучен вопрос, в каких кольцах вида a + b √‾+D имеет место однозначность разложения на простые множители, а в каких нет. Мы не будем на этом останавливаться.
Разложение целых чисел на множители напоминает другой раздел элементарной математики - разложение многочленов на множители. Этот раздел очень нравился нашему знакомому Васе Игнатьеву. Он умел разлагать на множители не только такие простые многочлены, как х² - 4= (х- 2) (х+ 2), но также способом группировки мог разложить:
х² - 3 х +2= х² - х- 2 х +2= х(х- 1)-2 (х- 1)= (х- 1 )(х- 2).
Эти примеры он брал из различных задачников. Однако, когда он попытался сам придумать пример и начал разлагать на множители многочлен х² +6х +4, у него ничего не вышло. Потом он сообразил, что даже многочлен х² - 2 не разлагается на множители. Он забросил листок, на котором решал пример, и нашел его только через год, когда перешел в следующий класс. «Над чем же я думал! - воскликнул он, - ведь
x² - 2= (х- √‾2) (х + √‾2), x² + 6 x+ 4= (х+ 3+ √‾5) (х+ 3- √‾5)».
Вася думал, что, научившись решать квадратные уравнения, он сможет разлагать на множители любой квадратный трехчлен. Но радость его была преждевременной; когда он взялся
414
за многочлен х² +6 х +10, то даже применение иррациональных чисел ему не помогло. При решении квадратного уравнения х² + 6 х +10=0 появились квадратные корни из отрицательных чисел, а про такие корни он еще ничего не знал.
Лишь в десятом классе Вася научился разлагать и такие многочлены - учитель рассказал о комплексных числах, после чего он смог решать все квадратные уравнения, а тем самым и разлагать на множители все квадратные трехчлены:
х² + 6 х+ 10= (х +3+ i)(x +3- i).
Почему же в разных классах Вася по-разному подходил к задаче о разложении многочлена, почему все больше расширялся класс многочленов, которые он мог разлагать на множители? Ларчик открывается просто - задача о разложении на множители не очень точно поставлена. Надо еще указать, какими могут быть эти множители, какими числами должны быть их коэффициенты. В седьмом классе Вася знал только рациональные числа. Поэтому он разлагал лишь на множители с рациональными коэффициентами. В восьмом классе он узнал иррациональные числа. Теперь он уже мог пользоваться и множителями с любыми действительными коэффициентами. Полное благополучие наступило в десятом классе, когда Вася стал встречаться с многочленами, коэффициенты которых комплексные. Таким образом, недостаточно сказать: «Разложите многочлен f(x) = а0 хn + а1 хn -1 ... + аn на множители». Надо еще сказать, какому полю должны принадлежать коэффициенты этих множителей.
Если все коэффициенты многочлена f(x) принадлежат числовому полю Р, то говорят, что f(x) является многочленом над полем Р. Например, х² + 6x+ 10 является многочленом над полем рациональных чисел, х² +2 х + p - над полем действительных чисел, а многочлен х² + ix +3- i - над полем комплексных чисел.
Разумеется, если поле Р является частью поля P1 (или, как говорят математики, его подполем), то любой многочлен над полем Р может рассматриваться и как многочлен над полем Р1. Ведь его коэффициенты принадлежат полю Р, а значит, и полю Р1. Такой подход бывает удобен при разложении многочленов на множители. Например, можно говорить о разложении многочлена x² +6 х+ 10 над полем комплексных чисел.
Разложение многочленов на множители похоже по своим свойствам на разложение целых чисел. Только вместо простых чисел надо брать так называемые неприводимые многочлены - те, которые нельзя представить в виде произведения двух многочленов меньшей степени (над заданным полем). Делителями единицы являются только многочлены нулевой степени, т. е. отличные от нуля числа. Как и для целых чисел, здесь каждый многочлен единственным образом разлагается в произведение неприводимых множителей. Разумеется, такие два разложения, как
х² + 3 х+ 2 =(х+ 1 )(х+ 2 )=( 2 х+ 2 )( 1 /2 х+ 1 ),
отличающиеся лишь делителями единицы, считаются одинаковыми.
Зачем же надо разлагать многочлены на множители? Одна причина ясна - для выполнения действий с алгебраическими дробями, Но есть и другая причина - разложение на множители облегчает решение уравнений. Пусть нам дано уравнение:
х 5 + 2 х 4 -х- 2 = 0.
Решать уравнения пятой степени мы не умеем. Но если сгруппировать члены в левой части, то получим:
(х+ 2) (х 4 - 1)=0. или:
(x+ 2)(x- 1)(x+ l)(x² + l) = 0.
А теперь видно, что левая часть обращается в нуль при x1 =- 2 , х2 =1, х3 =-1. Значит, эти числа являются корнями нашего уравнения. Других действительных корней у него нет, так как произведение может равняться нулю, лишь если какой-нибудь множитель равен нулю, а множитель х² + 1 при действительных х в нуль не обращается.
Вообще, если левая часть алгебраического уравнения f(x) =0 может быть записана в виде (х-а) р(х)= 0, где р(х) - тоже многочлен, то х = а является одним из корней нашего уравнения. Верно и обратное: если число а является корнем алгебраического уравнения f (x)=0, то многочлен f(x) делится без остатка на х-а. При этом если коэффициенты многочлена f(x)
415
и корень а принадлежат полю Р, то тому же полю принадлежат и коэффициенты многочлена р(х), ведь при делении многочленов «столбиком» мы выполняем над их коэффициентами лишь четыре арифметических действия. Особенно легко решать уравнения, левая часть которых разложена на множители первой степени:
(х-а1 )(х- a2) ... (x - an)=0.
В этом случае ясно, что корнями будут числа a1, а2,..., а n, а других корней не будет (так как если х отлично от всех чисел a1 , a2,..., a n, то ни один из множителей первой степени в нуль не обращается).
Верно и обратное: если мы знаем n корней al, а2,...,а n многочлена
f (х) = а0 хn + а1 х n-1 + ... +аn,
то он следующим образом разлагается на множители:
f (х) = а0 (х- a1 ) (х-а2 )...(х- аn).
Из сказанного ясно, что никакое уравнение n -й степени не может иметь больше, чем n корней. А имеет ли любое уравнение хотя бы один корень? Впрочем, эта задача опять нечетко поставлена: неясно, что значит «любое уравнение», какими должны быть его коэффициенты. Неясно и то, какие корни мы будем рассматривать.
Мы видели, что чем богаче элементами поле Р, тем больше возможностей разложить над ним заданный многочлен f(x) на множители. Например, многочлен х 4 - 2 совсем не разлагается над полем рациональных чисел, но разлагается на три множителя над полем действительных чисел:
Однако расширение поля влечет за собой и расширение множества многочленов, Которые надо разлагать. Ведь если допустить в качестве коэффициентов не только рациональные, но и действительные числа, то придется разлагать не только такие многочлены, как x 4 -2, но
и такие, как х 4 - √‾2, и даже такие, как х 4 - p. А если допустить комплексные числа, то придется рассматривать и многочлены вида х 4 + i .
К счастью, оказалось, что выигрыш от расширения поля больше, чем проигрыш, - над полем комплексных чисел любой многочлен (не только с рациональными, но и с любыми комплексными коэффициентами) разлагается до конца, т. е. на множители первой степени. А это означает, что всякое уравнение n -й степени с комплексными коэффициентами имеет ровно n корней. Эту теорему называют основной теоремой алгебры
многочленов. Ее доказал К. Гаусс в 1799 г.
Сложнее обстоит дело с разложением многочлена над полем действительных чисел. Как мы видели, над этим полем многочлен x² +6 x +10 не разлагается на множители первой степени. Однако любой многочлен с действительными коэффициентами, степень которого больше двух, всегда разлагается на множители с коэффициентами того же вида. Поэтому всякий многочлен с действительными коэффициентами разлагается над полем действительных чисел на множители первой и второй степеней.
Основная теорема алгебры дает только уверенность в том, что у каждого алгебраического уравнения есть корни. (Теоремы такого типа называют в математике теоремами существования.) Однако она ничего не говорит о том, как эти корни искать. Иными словами, вопрос о том, как решить данное уравнение, остается открытым и после доказательства основной теоремы.
Издавна люди занимались решением уравнений. При этом старались выразить корни уравнения через коэффициенты с помощью четырех арифметических действий и извлечения корней. Это удалось сделать для квадратных уравнений, а впоследствии и для уравнений третьей и четвертой степеней (см. статью «Как люди учились решать уравнения»).
Многие годы усилия математиков были направлены на то, чтобы найти решение в радикалах (т. е. с помощью этих же пяти действий) для любого уравнения пятой степени. Все эти попытки к успеху не привели. Долгое время думали, что дело в недостаточной изобретательности математиков и что когда-нибудь при-
416
дет математический гений, который решит задачу.
Гений действительно пришел, им был молодой норвежский математик Н. Абель. Однако вместо желанной формулы он дал отрицательный ответ - решения задачи не существует. Впрочем, сначала Абель ошибся (и гении делают
Нильс Генрик Абель.
ошибки!). Ему показалось, что он нашел формулу, дающую решение уравнения пятой степени в радикалах. Но потом он увидел ошибку, проанализировал свои рассуждения и в результате получил замечательный вывод: не только неверна выведенная им формула, но и вообще не существует общей формулы, выражающей корни любого уравнения пятой степени через коэффициенты этого уравнения с помощью сложения, вычитания, умножения, деления и извлечения корня.
На развитие теории уравнений сильное влияние оказали задачи о построениях циркулем и линейкой, в особенности задачи о построении правильных многоугольников. Из школьного курса известно, как строить циркулем и линейкой правильный треугольник, квадрат и шестиугольник. В более подробных курсах рассказано о построении правильного пятиугольника. А вот о построении правильного семиугольника или девятиугольника ничего
не говорится. И это не случайно: ни правильный семиугольник, ни правильный девятиугольник нельзя построить циркулем и линейкой.
Как же это узнали? Ведь доказать разрешимость задачи сравнительно легко - достаточно указать путь ее решения. Доказать же, что задачу нельзя решить, очень трудно. Путей решения задачи бесконечно много (мало ли какие построения можно придумать!), и доказать, что ни один из них не приведет к цели, на первый взгляд невозможно.
Однако математики справились с этой задачей. Для этого они сначала исследовали вопрос, какие отрезки можно построить циркулем и линейкой исходя из одного заданного отрезка (в случае построения правильного многоугольника заданным является радиус описанной окружности или сторона искомого правильного многоугольника).
Чтобы ответить на этот вопрос, пришлось ввести понятие квадратичной иррациональности. Так назвали числа, которые получаются из единицы с помощью четырех арифметических действий и операции извлечения квадратного корня. Вот для примера некоторые числа, являющиеся квадратичными иррациональностями:
Все квадратичные иррациональности, вместе взятые, образуют числовое поле, причем в этом поле всегда выполнима операция извлечения квадратного корня из положительного числа.
Было доказано, что если задан отрезок а, длина которого принимается за единицу, то циркулем и линейкой можно построить любые отрезки, длины которых являются квадратичными иррациональностями, и только эти отрезки.
Например, для построения правильного пятиугольника с данной стороной достаточно построить его диагональ (тогда все вершины можно будет найти с помощью засечек окружности). Расчеты показывают, что если сторона пятиугольника равна 1, то его диагональ имеет длину
(√‾5 +1)/2. Так как это число является квадратичной иррациональностью, то построение правильного пятиугольника с помощью циркуля и линейки возможно.
417
А вот правильный девятиугольник построить нельзя. Его построение сводится к делению угла в 120° на три равные части. По формулам тригонометрии:
cos3 j =4 cos³ j - 3 cos j .
Положим здесь 3 j =120°. Так как cos 120°= 1/2,
то для отыскания cos j получим кубическое уравнение:
4 cos³ j - 3 cos j+1 /2 =0,
или, полагая 2 cos j = x, получим уравнение:
x³ - 3 х +1=0. (3)
Было доказано, что если один из корней кубического уравнения с целыми коэффициентами является квадратичной иррациональностью, то у него есть и рациональный корень. А легко доказать, что у уравнения (3) рациональных корней нет, значит, нет и корней, являющихся квадратичными иррациональностями. Поэтому и нельзя построить правильный девятиугольник циркулем и линейкой. (Поскольку угол в 120° нельзя разделить циркулем и линейкой на три равные части, тем более нельзя указать метод деления циркулем и линейкой на три равные части для произвольного угла. Для некоторых углов, например 90°, эта задача разрешима.) Точно так же доказывается невозможность построения циркулем и линейкой правильного семиугольника.
Окончательное решение вопроса о построении правильных многоугольников циркулем и линейкой дал в 1796 г. Гаусс. Он доказал,
что если р - простое число, то правильный р-угольник с данной стороной может быть построен циркулем и линейкой в том, и только в том, случае, когда число р можно записать в виде р=2² n +1, где n - целое число. Например, при n =0 имеем р =3, а при n =1 имеем р= 5. Поэтому правильный треугольник и правильный пятиугольник можно построить циркулем и линейкой. При n= 2 получаем р =17. Значит, и правильный семнадцатиугольник строится циркулем и линейкой. Можно построить циркулем и линейкой даже правильные многоугольники с 257 и 65536 сторонами. А вот при n= 5 число 2² n +1 оказывается составным. Поэтому правильный (2 2 5 +1)-угольник нельзя построить циркулем и линейкой.
В древности математики потратили много сил на решение следующей задачи об удвоении куба: дан куб со стороной а ; построить такой куб, объем которого вдвое больше объема данного куба. Подсчитаем, какой отрезок надо построить для решения этой задачи. Примем длину отрезка а за единицу, а длину ребра искомого куба обозначим через х. Тогда объем данного куба будет равен единице, а объем искомого куба - двум. По условию задачи должно быть: х³ =2. Это уравнение не имеет рациональных корней. Поэтому по упомянутой выше теореме у него нет и корней, являющихся квадратичными иррациональностями. Значит, решить задачу удвоения куба циркулем и линейкой невозможно.
Гораздо труднее было доказать, что невозможно построить циркулем и линейкой квадрат, равновеликий кругу радиуса 1 (задача о квадратуре круга). Это доказательство было проведено неалгебраическими методами. Было доказано, что сторона такого квадрата не только не является
418
квадратичной иррациональностью, но даже не может быть корнем никакого алгебраического уравнения с целыми коэффициентами (такие числа называют неалгебраическими или трансцендентными).
О том, что такое геометрические преобразования и как они применяются для решения задач, было подробно рассказано в статье «Геометрические преобразования». На первый взгляд может показаться, что эта область математики относится целиком к геометрии, а алгебраистам там делать нечего. Но это не так; оказывается, геометрические преобразования можно умножать, а ведь алгебра изучает свойства самых различных действий, в том числе и умножения преобразований.
Как же умножить геометрическое преобразование а на геометрическое преобразование b ? А очень просто - сначала сделать преобразование а, а потом р. В результате получится новое преобразование. Его называют произведением преобразований a и b и обозначают ар" Пусть, например, a - поворот плоскости вокруг точки О на 30°, а b - поворот вокруг той же точки на 45°. Сделав эти повороты один за другим, получим поворот плоскости вокруг точки О на 75°. Этот поворот и является произведением поворотов a и b .
Умножение преобразований похоже по своим свойствам на умножение чисел. Напри-
мер, для умножения преобразований верен ассоциативный закон:
a (b g)=(a b) g
(и a (b g), и (a b) g сводятся к последовательному применению преобразований a, b, g). Есть и преобразование, играющее роль единицы, т. е. такое, что для любого преобразования a верна формула a ·е = е· a = a. Им является тождественное преобразование е, оставляющее все точки на месте. Ясно, что если сначала сделать преобразование е, т. е. оставить все неизменным, а потом преобразование а, то это все равно что сделать только преобразование а. Поэтому е· a = a. Точно так же доказывается, что a ·е= a .
- А нужно ли доказывать последнее равенство?- спросит читатель. - Ведь уже доказано, что е· a = a, а от перестановки сомножителей произведение не меняется. Вспомните, однако, что при умножении кватернионов переставлять слагаемые нельзя. Оказывается, их нельзя переставлять и при умножении преобразований. Вот простой пример.
Пусть а - сдвиг вдоль оси Ох на 6 единиц, а b -поворот на 90° вокруг точки О. При преобразовании а начало координат перейдет в точку А (6; 0). При преобразовании b (т. е. при повороте на 90°) точка А перейдет в точку 5(0; 6). Таким образом, преобразование a · b переводит точку О в точку В. Произведем теперь те же преобразования в обратном порядке. При повороте а точка О останется на месте. При сдвиге же b точка О перейдет в точку А. Значит, b · a переводит О в точку А, а не в точку В. Мы видим, что a · b ¹ b · a .
Итак, умножение преобразований не обладает свойством коммутативности. Выполнение равенства a b = b a является для преобразований не правилом, а исключением. Одно из таких исключений дается формулой: a е=е a .
419
Преобразования можно не только умножать, но и делить друг на друга. Для чисел деление сводится к умножению на обратное число, на-
пример: 2:5=2· 1/2 =2·5-1. И для преобразований деление сводится к умножению на обратное преобразование. Это преобразование определяют следующим образом.
Пусть преобразование а переводит точку Р в точку Q. Тогда обратное ему преобразование a-1 переводит Q обратно в точку Р. Например, если a - сдвиг вправо на отрезок а, то a-1 сдвиг влево на тот же отрезок а.
Ясно, что если сначала сделать преобразование a, а потом преобразование a-1, то в результате все точки вернутся на свои места и получится тождественное преобразование. Поэтому a · a-1 = е. Точно так же a-1 · a = е.
Теперь ясно, как можно делить преобразования. Только, в отличие от чисел, для преобразований есть два вида деления - слева и справа. Если разделить преобразование а слева на b, то получится b-1 a, если справа - то a b-1 .
Зачем же нужно умножать преобразования? Чтобы разобраться в этом, разберемся в понятии равенства геометрических фигур.
В статье «Геометрические преобразования» рассказано, что две геометрические фигуры называются равными, если существует движение, при помощи которого можно совместить одну фигуру с другой. Геометрические свойства равных фигур совершенно одинаковы. Поэтому можно сказать, что геометрия изучает
Рис.3.
только те свойства фигур, которые не меняются при движениях.
Однако это определение не всегда удовлетворительно. Например, при изучении векторов (а теория векторов - это часть геометрии) два вектора считают равными, если не только их длины одинаковы, но и векторы параллельны и одинаково направлены. Поэтому, например,
векторы ОА→ и О B→ (рис.2) не считаются равными, хотя один из них получается из другого
поворотом вокруг точки О. А векторы ОА→ и CD→ на том же рисунке равны друг другу. Чтобы
получить вектор CD→ из вектора ОА→, надо сделать параллельный перенос плоскости на вектор ОС→ .
Таким образом, два вектора называются равными, если один получается из другого с помощью параллельного переноса. Можно сказать, что векторная алгебра изучает свойства, остающиеся неизменными при параллельных переносах.
В других случаях приходится изучать свойства фигур, остающиеся неизменными лишь при поворотах вокруг некоторой точки. Если, например, инженеру надо рассчитать турбину (рис.3), то для него все лопатки турбины равноправны - одна получается из другой поворотом вокруг оси турбины. А сместить лопатку вдоль радиуса нельзя - при этом изменится центробежная сила и весь расчет окажется неверным.
Точно так же две фигуры на сфере надо считать равными, если одна получается из другой поворотом вокруг центра сферы.
Можно привести и такие случаи, когда целесообразно считать равными геометрические фигуры, не являющиеся таковыми с обычной точки зрения. Например, при изучении угловых свойств окружности можно полностью отвлечься от ее размеров. Тогда все окружности будут для нас одинаковыми. Но окружность S1
420
на рис.4 нельзя перевести в окружность S2 движением. Для этого надо применить более общее преобразование подобия. Существуют и такие случаи, когда целесообразно считать равными фигуры, переводимые друг в друга аффинными преобразованиями, проективными и т. д. (см. об этом подробнее в статье «Геометрические преобразования»).
Поэтому можно дать такое определение равенства геометрических фигур. Пусть имеется некоторое множество геометрических преобразований G. Фигура F1 называется равной фигуре F2 относительно этого множества пре-
образований, если есть преобразование a из G, переводящее F1 в F2. Например, если множество G состоит из параллельных переносов, то фигуры F1 и F2 на рис.5 равны, а фигуры F1 и F3 не равны. Если же множество G состоит из поворотов вокруг точки О, то равными окажутся фигуры Р1 и F3, а неравными - F1 и F2. Наконец, если взять множество всех движений
плоскости, то относительно него все три фигуры равны.
Ясно, что чем больше преобразований содержит множество G, тем большее число фигур окажется равным относительно этого множества преобразований.
Не всякое множество G геометрических преобразований пригодно для определения равенства фигур. Ведь может случиться, что в множестве G отсутствует преобразование, оставляющее какую-то фигуру F неизменной. Тогда окажется, что эта фигура не равна самой себе. Конечно, такое определение равенства никуда не годилось бы. Поэтому потребуем, чтобы среди преобразований множества G было тождественное преобразование е, т. е. такое, при котором все фигуры остаются неизменными. Тогда любая фигура будет равна самой себе относительно этого множества.
Но существования тождественного преобразования еще мало. Может случиться, что в множестве G есть преобразование, переводящее фигуру F1 в фигуру F2, есть и преобразование, переводящее фигуру F2 в фигуру F3, но нет преобразования, переводящего F1 прямо в F3. Тогда получится, что F1 =F2 , F2 =F3, но F1 ¹ F3
Чтобы избежать этой неприятности, введем следующее условие: вместе с любыми двумя преобразованиями a и b в множество G входит и их произведение ар.
Наконец, надо, чтобы из равенства F1 =F2 вытекало равенство F2 = F1. Иными словами, надо, чтобы вместе с преобразованием, переводящим фигуру F1 в фигуру F2, множество G содержало и преобразование, переводящее F2 в F1. Для этого достаточно, чтобы вместе с преобразованием а множество G содержало и обратное ему преобразование a-1 .
Подведем итоги. Для того чтобы равенство геометрических фигур, определенное с помощью множества преобразований G, обладало «хорошими» свойствами, нужно следующее: 1) множество G должно содержать тождественное преобразование; 2) вместе с двумя преобразованиями a и b в G должно входить их произведение a b ; 3) вместе с каждым преобразованием а множество G должно содержать обратное к нему преобразование a-1 .
Множество преобразований, для которого выполнены эти три условия, называют группой геометрических преобразований.
Таким образом, для того чтобы с помощью множества G геометрических преобразований можно было определить понятие равенства геометрических фигур, надо, чтобы это множество было группой.
421
До того времени, пока математики не поняли, что равенство геометрических фигур можно определять при помощи различных групп геометрических преобразований, казалось, что существует только одна геометрия, а именно та, которую изучают в школе. Первый удар этому мнению нанес Н. И. Лобачевский, который построил новую геометрию, совсем не, похожую на обычную (см. статью «О различных геометриях»). Истинную причину различия геометрии Лобачевского и геометрии Евклида впервые глубоко осветил немецкий математик Ф. Клейн. Он показал, что все дело в различии групп преобразований, используемых в этих геометриях для определения равенства фигур: в геометрии Евклида для этого используется группа обычных движений, а в геометрии Лобачевского совершенно другая группа преобразований (их называют гиперболическими движениями плоскости).
Вообще, каждая группа преобразований плоскости определяет свое понятие равенства, а значит, и свою геометрию, В геометрии, соответствующей некоторой группе преобразований, изучаются лишь свойства, одинаковые у всех фигур, равных относительно этой группы. Иными словами, изучаются те геометрические свойства фигур, которые сохраняются при всех преобразованиях рассматриваемой группы. Эту точку зрения на геометрию впервые четко сформулировал Ф. Клейн в 1872 г. на лекции в г. Эрлангене. С тех пор такой подход к пониманию геометрии получил название эрлангенской программы.
Теоремы школьной геометрии тоже фактически относятся к различным геометриям. Одни из них касаются свойств фигур, не меняющихся при движениях, а другие - более глубоких свойств, не меняющихся при любых аффинных преобразованиях и даже любых проективных преобразованиях (см. подробнее об этом статью «Геометрические преобразования»).
Посмотрите на геометрические фигуры, изображенные на рис.6. Фигуру А на этом рисунке никак нельзя назвать симметричной. Фигуры В и С уже обладают некоторой симметрией, Более симметрична фигура D, и, конечно, самой симметричной из всех начерченных фигур является квадрат. Однако это только слова - симметричность не длина и не площадь, а потому понятия «больше» и «меньше» для оценки симметричности пока точного смысла не имеют.
Как же можно оценить большую или меньшую симметричность фигуры? Для этого надо рассмотреть множество всех движений плоскости, которые переводят рассматриваемую фигуру самое в себя. Для фигуры А на рис.6 единственным таким движением является тождественное преобразование. Для фигур В и С, кроме тождественного преобразования, есть еще по одному движению, переводящему их в себя. Именно, для равнобочной трапеции - осевая симметрия (относительно прямой, соединяющей середины оснований), для параллелограмма - центральная симметрия. Для ромба D есть уже 4 движения, совмещающих его с самим собой: тождественное преобразование, две осевые симметрии относительно диагоналей и центральная симметрия. Наконец, для квадрата таких преобразований 8 (4 осевые симметрии
относительно средних линий и диагоналей и 4 вращения на углы 0°, 90°, 180° и 270°).
Ясно, что совокупность всех движений, переводящих заданную геометрическую фигуру самое в себя, образует группу. В самом деле,
422
если преобразования a и b переводят фигуру F в себя, то и их произведение a · b преобразует ее в себя. Не изменит ее, конечно, и тождественное преобразование. То же самое верно и для обратного преобразования. Группу всех движений, переводящих фигуру F самое в себя, называют группой симметрии этой фигуры.
Чем шире группа симметрии данной фигуры, тем более симметричной она является. Именно поэтому квадрат является наиболее симметричной из всех фигур, изображенных на рис.6. Интересные примеры симметричных фигур, обладающих самыми разными типами симметрии, дают узоры (см. цветную вклейку на стр. 396-397).
Если фигура переходит сама в себя при
(360° · k) /n всех поворотах на углы вида, где
k - целое, а n - фиксировано, то говорят, что она обладает симметрией порядка п. Такой симметрией обладает, например, правильный n -угольник.
Бывают фигуры, у которых группа симметрии бесконечна. Примерами могут служить окружность, кольцо, а также фигуры, изображенные на стр. 424-425 (эти фигуры надо представлять себе простирающимися в бесконечность).
Разумеется, о группе симметрии можно говорить не только для плоских, но и для пространственных фигур. При этом обычно рассматривают только движения пространства, не являющиеся симметриями относительно плоскостей (их нельзя осуществить в пространстве движениями пространственных тел как твердого целого). Так, можно говорить о группе симметрии правильного тетраэдра, куба, икосаэдра, правильной n -угольной призмы и т. д. Предоставляем читателю убедиться, что группа симметрии куба состоит из 24 элементов, а для правильной n -угольной призмы из 2 n элементов.
Используя группу симметрии куба, легко решить интересную задачу о раскраске куба. Пусть дан куб и 6 красок: синяя, зеленая, желтая, красная, коричневая и черная. Сколькими различными способами можно раскрасить 6 граней куба этими красками так, чтобы все грани имели различный цвет?
Для решения занумеруем грани куба. Тогда
первую грань можно раскрасить 6 различными способами. Если выбрана окраска первой грани, то для второй грани остается 5 цветов. Всего первые две грани можно раскрасить 6·5=30 способами. Точно так же видно, что первые три грани можно окрасить 6·5·4=120 способами, а весь куб - 6·5·4·3·2·1=720 способами.
А теперь выясним, сколько из этих способов геометрически различны. Именно, назовем две окраски куба геометрически совпадающими, если одна получается из другой движением куба как твердого тела. Так как группа симметрии куба состоит из 24 элементов, то число окрасок, геометрически совпадающих с данной (включая ее саму), равно 24. Следовательно, число геометрически различных окрасок куба в 24 раза меньше, чем общее число окрасок, т. е. 720:24=30.
Симметрией обладают не только геометрические фигуры или вещи, сделанные рукой человека, но и многие творения природы (бабочки, стрекозы, листья, морские звезды, снежинки и т. д.). Особенно разнообразны свойства симметрии кристаллов. На стр. 424-425 показаны некоторые виды кристаллов. Одни из них более симметричны, другие - менее. Долгое время ученые-кристаллографы не могли описать всех видов симметрии кристаллов. Решил эту задачу в 1890 г. русский ученый Е. С. Федоров. Он доказал, что есть ровно 230 групп, переводящих в себя кристаллические решетки. Это открытие значительно облегчило кристаллографам изучение видов кристаллов, которые могут существовать в природе.
Следует, однако, заметить, что многообразие кристаллов в природе настолько велико, что даже использование группового подхода
423
не дало еще способа описать все возможные формы кристаллов.
Очень широко используется теория групп симметрии в квантовой физике. Уравнения, которыми описывается поведение электронов в атоме (так называемое волновое уравнение Шредингера), уже при небольшом числе электронов настолько сложны, что непосредственное решение их практически невозможно. Однако, используя свойства симметрии атома (неиз менность электромагнитного поля ядра при поворотах и симметриях, возможность перестановки некоторых электронов между собой, т. е. симметричное расположение этих электронов в атоме, и т. д.), удается исследовать их решения, не решая уравнений.
Евграф Степанович Федоров.
Вообще, использование теории групп является мощным математическим методом исследования и учета симметрии явлений природы.
Преобразования можно производить не только над геометрическими фигурами, но и над алгебраическими выражениями. Речь идет здесь, конечно, не о тождественных преобразованиях (раскрытии скобок, приведении подобных членов и т. д.). Нет, мы будем рассматривать
такие преобразования, как изменение знаков переменных, перестановки переменных и т. д. Например, многочлен
х³ - y² +3 xy 4
при изменении знаков переменных х и у превращается в многочлен
- x³ - у² - 3 xy 4,
а при перестановке х и y - в многочлен
у³ -х² + 3 yx 4 .
Изучение преобразований алгебраических выражений представляет собой, с точки зрения эрлангенской программы Ф. Клейна, своеобразную геометрию. В этой геометрии «фигурами» являются алгебраические выражения (многочлены, дроби и т. д.), а группа преобразований состоит в одних случаях из всевозможных перестановок переменных, в других - из циклических перестановок переменных (при которых каждое переменное заменяется следующим, а последнее - первым), в третьих - из всевозможных замен знаков переменных (рис.7) и т. д.
Вопросы симметрии относятся не только к геометрии, но и к алгебре. На рисунке показана фотография Атомиума - здания павильона на Всемирной выставке в Брюсселе (1958 г.), имеющего форму атома железа. Пятиконечная звезда обладает симметрией 5-го порядка и, кроме того, симметричная относительно прямых, соединяющих центр звезды с ее вершинами. Симметрична и кристаллическая решетка алмаза. Снежинка, кроме симметрии 6-го порядка, симметрична и относительно 6 осей (каких?). Бокалы переходят в себя при любом вращении вокруг оси, а сосуды, украшенные орнаментом, только при вращении на определенные углы (другие вращения смещают узор). Очень много осей симметрии у зубчатого колеса. Симметрия часто используется в архитектуре.
Многообразны формы симметрии кристаллов.
424
Задачей такой геометрии, как и обычной геометрии, является нахождение таких свойств «фигур» (т. е. алгебраических выражений), которые сохраняются при всех преобразованиях данной группы. В частности, весьма интересно нахождение и изучение «симметричных фигур» для данной группы, т. е. алгебраических выражений, которые не изменяются при преобразованиях данной группы. Например, если рассматривать группу всех перемен знаков, то «симметричными фигурами» будут четные выражения, т. е. такие, у которых показатели всех степеней переменных четны (например, х² +у 4 , х² +5- x 8 y 6, (x2 - y²)/ x 4 + y 4) и т. д.)
Для группы всех перестановок переменных «симметричными фигурами» будут такие выражения, которые не меняются ни при каких перестановках переменных. Они называются симметрическими функциями. Например, симметрическими многочленами от двух переменных х, у являются:
x² y² - x 4 - y 4 , х² +ху+ y², х 5 + y5, ху³ +х³ у.
В такой геометрии есть и свои теоремы. Например, можно доказать, что любой симметрический многочлен от х и у выражается через два простейших многочлена х+у и ху. Например:
х 5 +у 5 = (х + y) 5 - 5 (х+у)³ ху+ 5 (х+у)(ху)² .
Эту теорему можно применять при решении систем уравнений. Если оба уравнения системы двух уравнений с двумя неизвестными симметричны относительно х и y, то бывает полезно ввести новые неизвестные: u = х+у, v = ху. Как правило, после этого заданная система уравнений упрощается. Например, система уравнений
при такой замене сводится к системе
Из этой системы легко найти u и v, а потом x и y .
Любопытно, что теория групп первоначально и возникла при рассмотрении групп алгебраических преобразований Чтобы узнать, решается ли данное алгебраическое уравнение
хn +а1 хп -1 + ...+ аn =0 (4)
в радикалах, алгебраисты стали рассматривать значения, которые принимают многочлены от n переменных, если в них вместо x1; x2, ..., хn подставить корни a1, a2, ..., a n уравнения (4). Оказалось, что вопрос о разрешимости уравнений в радикалах тесно связан с поведением этих значений многочленов при различных перестановках корней между собой.
Эти исследования привели к созданию новой, очень глубокой и важной ветви алгебры - применению теории групп к исследованию уравнений. Основоположные результаты этой теории были получены в 1830-1832 гг. французским математиком Э. Галуа. В его честь весь этот раздел алгебры носит сейчас название теории Галуа.
Рассмотрим следующие две группы преобразований. Первой из них является группа симметрии ромба, второй - группа перемен знаков переменных х и у. Обозначим тождественное преобразование ромба через е, симметрии относительно диагоналей - через а и b и центральную симметрию - через с. Проверьте, что «таблица умножения» в этой группе имеет следующий вид:
Теперь обратимся к группе перемен знаков у переменных х и у. Здесь мы также обозначим тождественное преобразование х → х, у → у через е. Изменение знака у одного только х (т. е. преобразование х → -х, у → у) обозначим через а, а изменение знака у одного только у - через b . Наконец, преобразование х → - x, у → -у (изменение знаков у обоих переменных) обозначим через с. Легко проверяется
425
тогда, что в рассматриваемой группе преобразований «таблица умножения» имеет вид:
Сразу бросается в глаза, что написанные «таблицы умножения» совершенно одинаковы. Итак, различные группы преобразований могут оказаться совершенно одинаково устроенными, т. е. иметь одинаковое число элементов и одинаковую таблицу умножения. Для решения многих вопросов, относящихся к группам преобразований, совершенно неважно знать, что именно преобразуется, а существенно лишь, сколько имеется различных преобразований в группе и как они перемножаются.
Отто Юльевич Шмидт.
Изучением групп с этой точки зрения занимается так называемая абстрактная теория групп. В этой теории рассматривают множества G, состоящие из каких угодно элементов (не обязательно преобразований), для которых определено каким-то образом умножение, обладающее следующими свойствами:
1. Произведение ab двух элементов из G принадлежит G.
2. Существует элемент е (единичный), обладающий тем свойством, что для всех элементов а из G выполняется равенство ае=а.
3. Для любого элемента а есть обратный ему элемент а -1, т. е. такой, что аа -1 = е.
4. Для любых трех элементов а, b, с выполнено равенство а(b с)=(а b)с.
Заметим, что последнее равенство, выражающее ассоциативность умножения, всегда выполняется для преобразований.
Множество G с указанными свойствами называется группой. Первая в России книга по теории групп вышла в 1916 г. и принадлежит перу О. Ю. Шмидта.
Значение абстрактной теории групп состоит в том, что теоремы и понятия этой теории могут применяться и к группам геометрических преобразований, и к группам алгебраических преобразований, и к изучению атомов и кристаллов и т. п.
Мы рассмотрели различные вопросы, изучаемые в алгебре. Все эти вопросы объединяются одним общим направлением - изучением общих свойств действий и преобразований. Алгебра и дает аппарат изучения этих свойств. Законы действий (т. е. аксиомы, которым они подчиняются) могут быть совершенно различными, в зависимости от поставленной задачи. В соответствии с этим получаются группы, кольца, поля и т. п.
В современной алгебре рассматриваются и другие объекты, подчиненные совсем иным аксиомам (алгебры Ли, альтернативные алгебры, полугруппы и т. д.). Не следует думать, однако, что работа алгебраиста заключается в выписывании новых, произвольно взятых аксиом и выяснении их следствий. Как правило, интересные алгебраические объекты получаются не таким путем. Интересные объекты возникают при рассмотрении глубоких задач геометрии, физики, математического анализа, логики и самой алгебры. При изучении этих задач исследователь, отбрасывая второстепенное и несущественное, выделяет важное и основное и формулирует общие свойства различных объектов в виде аксиом. Таким образом, и в алгебре аксиомы имеют опытное происхождение (хотя это и не всегда может быть непосредственно замечено).
426
Человек создает машины, чтобы облегчить труд. И они безотказно помогают шахтерам и кузнецам, колхозникам и землекопам. Но вот могут ли они принести пользу математикам, приняв на себя хотя бы часть их работы?
Еще 25-30 лет назад в ответ на такой вопрос последовало бы решительное «нет»: уж очень трудно было вообразить себе машину на поприще умственного труда!
Теперь положение изменилось. С каждым днем повышается роль науки - она стала уже непосредственной производительной силой общества. Работникам умственного труда приходится сталкиваться теперь с такими проблемами, которые для «невооруженного» мозга не только отдельного человека, но даже и целого коллектива оказываются непосильными. Если раньше для ускорения вычис-
427
Рис.1. Общий вид электронной вычислительной машины.
лений довольствовались такими простыми приспособлениями, как счеты, арифмометр, логарифмическая линейка, то теперь этого уже недостаточно. Ведь считая на арифмометре, не сделаешь в минуту больше трех действий над многозначными числами, а расчет атомного реактора включает в себя более 6 млрд. арифметических действий. Значит, на этот расчет понадобится 2 млрд. минут; а ведь первый миллиард минут с начала нашей эры истек только 29 апреля 1902 года! Еще труднее поспевать вычислителям при запуске космических кораблей: они должны выдавать результат очень сложных расчетов почти мгновенно, пока ракета не успела еще значительно отклониться от заданной траектории.
Немало задач, превышающих возможности человеческого мозга, возникает и внутри самой математики. Как некоторые физические работы немыслимо выполнять вручную, так не могут быть решены «вмозговую» и некоторые важные проблемы из области умственного труда.
На помощь приходят электронные вычислительные машины (рис.1).
Электронная вычислительная машина по сравнению с простым арифмометром - это все равно, что современный завод по сравнению с напильником.
Прежде всего, арифмометр и подобные ему простые вычислительные приборы слишком медлительны. Колеса с зубьями и другие механические детали чересчур инерционны и даже при использовании моторов не могут срабатывать с желательной быстротой. Вот если бы удалось заменить механические детали какими-нибудь электронными приборами, тогда работа арифмометра стала бы молниеносной. Ведь успевает же электронный луч прочертить на экране телевизора 625 строк за 0,04 секунды!
Электроника умеет уже заменять быстродействующими электронными лампами медлительные механические устройства. Но сразу же нужно принять во внимание одно существенное различие между зубчатым колесом и электронной лампой. Колесо с 10 зубцами имеет 10 четко фиксированных положений, которые могут быть сопоставлены с цифрами от 0 до 9. У электронной же лампы есть только два резко различных состояния: как говорят радисты, она может быть «заперта» или «открыта». Запертая лампа совсем не пропускает тока, так как на ее управляющую сетку подано достаточно большое отрицательное напряжение; открытая лампа пропускает через себя максимально возможный ток (благодаря наличию на сетке достаточного положительного потенциала). Все промежуточные состояния лампы (когда она «полуоткрыта») недостаточно устойчивы и не могут служить для изображения цифр (изменение свойств лампы с течением вре-
428
мени или от внешних причин привело бы к замене одной цифры другой).
Используя два резко различных состояния электронной лампы, возможно изобразить только две цифры: например, 0 (лампа заперта) и 1 (лампа открыта). Поэтому при замене зубчатых колес арифмометра электронными лампами естествен также и переход от десятичной системы нумерации к двоичной (позволяющей записать любое число в виде определенной комбинации нулей и единиц).
В статье «Как люди считали в старину и как писали цифры» уже говорилось, что в двоичной системе нумерации обходятся двумя цифрами: нулем и единицей. Единица каждого следующего разряда числа в двоичной записи в два раза больше единицы предыдущего разряда: две «простые» единицы составляют двойку, две двойки - четверку, две четверки - восьмерку, две восьмерки - шестнадцать и т. д.
Число «один» записывается как обычно - «1». Но число «два» составляет уже единицу второго разряда и потому записывается так: «10» (одна двойка и нуль единиц). Число «три» изображается: «11» (одна двойка и одна единица). Число «четыре» представляет собой единицу третьего разряда и потому записывается «100» (одна четверка, нуль двоек и нуль единиц). Дальнейшие числа в двоичной записи имеют вид:
пять - «101» (одна четверка, нуль двоек и одна единица),
шесть - «110» (одна четверка, одна двойка и нуль единиц),
семь - «111» (одна четверка, одна двойка и одна единица).
Восьмерка - это опять новый разряд - «1000» (нули указывают на отсутствие четверок, двоек и единиц). Далее идут:
девять - «1001» (одна восьмерка и одна единица),
десять - «1010» (одна восьмерка и одна двойка),
одиннадцать - «1011» (т. е. 8+2+1),
двенадцать - «1100» (т. е. 8+4),
тринадцать - «1101» (т. е. 8+ 4+1) и т. д.
Вот перед нами «загадочное» число:
1001011
Рис.2. Числа «10110» и «01010» на перфокарте.
записанное в двоичной нумерации. Его легко «разгадать», подписав (справа налево) под каждым разрядом его значение:
Как видим, заинтересовавшее нас число складывается из единицы, двойки, восьмерки и шестидесяти четырех (1+2+8 + 64). Очевидно, оно равно 75. Читатель, вероятно, теперь уже сам сможет определить, что двоичной записью 10110011 изображается число 179.
Одно из преимуществ двоичной записи - удобство изображения чисел разнообразными средствами и быстрой передачи их из одного места в другое. Например, пробитый квадратик особой картонной карточки (ее называют перфокартой) может изображать единицу, а целый - нуль (рис.2). Поместив перфокарту между пружинящими контактами электрической цепи (рис.3), мы получим в ней ток, если в данном квадратике записана единица (контакты замкнутся через отверстие), и наоборот: если в данном квадратике записан нуль, тока в цепи не будет (рис.4), так как картонная прокладка изолирует контакты друг от друга.
Кратковременный электрический ток принято называть электрическим импульсом. Как видим, любое число, записанное по двоичной системе, легко может быть выражено последовательностью электрических импульсов, причем наличие импульса в определенный момент времени означает единицу, а отсутствие его - нуль. Впрочем, иногда предпочитают изображать нуль не отсутствием импульса, а импульсом тока, идущего в противоположном направлении (в этом случае не обязательно уже выдерживать строго определенные промежутки времени между импульсами). Продолжительность импульса может быть очень малой, скажем, в 1 микросекунду (т. е. миллионную долю секунды), что дает возможность передать даже многозначное число почти мгновенно.
429
Рис.3. Контакт обнаружил «единицу»: идет ток.
Рис.4. Обнаружен «нуль»: тока нет.
Арифметика чисел в двоичной записи очень проста. Вся таблица умножения сводится к четырем простейшим произведениям:
0x0=0, 1x0=0,
0x1=0, 1x1=1,
а таблица сложения - к четырем столь же простым суммам. Не правда ли, это не особенно далеко выходит за пределы прославленных познаний Митрофанушки из комедии Фонвизина?
Нетрудно придумать прибор, который будет выполнять умножение согласно этой таблице. Проще всего использовать для этой цели последовательное соединение двух электронных ламп (рис.5). Цифры сомножителей изображаются короткими импульсами электрического напряжения: единица положительным, а
нуль - отрицательным. Импульс первого сомножителя подается на сетку одной лампы, а импульс второго сомножителя - на сетку другой.
При перемножении двух единиц обе лампы отпираются соответствующими этим единицам положительными импульсами напряжения, и в их общей анодной цепи идет ток. Импульс
этого тока как раз и изображает «на электронном языке» единицу произведения (1x1=1). Если же хотя бы один из сомножителей- нуль, соответствующая лампа заперта отрицательным напряжением на ее сетке, и никакого импульса тока в анодной цепи не будет. А это как раз и является выражением нулевого значения произведения - в полном соответствии с формулами:
·1x0=0, 0x1=0, 0x0=0.
Как видим, «электронное перемножение» однозначных чисел осуществляется очень просто. Для многозначных сомножителей схему приходится, конечно, значительно усложнить, но нас интересует сейчас только принципиальная сторона дела, а не технические подробности. Подобно тому как подходящая комбинация зубчатых колес в арифмометре дает возможность выполнять арифметические действия, надлежащее сочетание электронных ламп позволяет производить эти действия над числами, заданными в виде последовательности электрических импульсов.
Рис.5. Электронный перемножитель.
Их можно «электронным способом» складывать, вычитать, умножать, делить, сравнивать между собой (определяя, которое из них больше) и т. д. Любое из этих действий осуществляется очень быстро, так как электронные лампы практически безынерционны. Еще большие возможности открывают появившиеся недавно различные заменители электронных ламп: полупроводниковые, ферритовые, сверхпроводящие и иные приборы.
Итак, налицо реальная возможность создать электронный арифмометр, способный выполнять любое арифметическое действие, скажем, за микросекунду. Но это еще далеко не электронная вычислительная машина, а только бы-
430
стродействующий арифмометр, практическое значение которого очень невелико. Как вы думаете, сколько действий можно было бы выполнить на таком быстродействующем арифмометре за каждую секунду? Миллион ? Или хотя бы тысячу?
Это зависит, конечно, от того, сумеем ли вы достаточно быстро задавать этому арифмометру задачи и записывать получающиеся результаты. Ведь если мы будем все это проделывать вручную, то больше 3-4 действий в минуту выполнить не удастся. Фантастическое быстродействие арифмометра окажется совершенно бесполезным.
Чтобы электронный арифмометр действительно выполнял за каждую секунду хотя бы несколько тысяч действий, необходимо полностью автоматизировать весь вычислительный процесс, совершенно исключив из него участие человека. Электронная вычислительная машина - это не просто быстродействующий арифмометр, а быстродействующий арифмометр плюс электронный автомат, который заменяет человека, работающего на арифмометре.
Чтобы легче понять, как может быть такой автомат создан, присмотримся повнимательнее к работе человека-вычислителя в каком-нибудь вычислительном бюро, не располагающем электронной вычислительной машиной.
Вычислитель должен иметь образование в объеме средней школы и хорошо уметь обращаться с простейшими вычислительными приборами (например, с арифмометром). Совсем не обязательно, чтобы вычислитель понимал научную или инженерную суть тех расчетов, которые ему поручены. Весь план расчетов составляется учеными или конструкторами, а вычислителю дается только список исходных данных и специальная инструкция, определяющая порядок действий. Согласно этой инструкции он и действует; при этом все арифметические операции выполняются на арифмометре, промежуточные результаты записываются на специальном бланке, а окончательные заносятся в другой бланк.
Простейший пример - составление таблицы значений площади круга в зависимости от его радиуса (по формуле S = π r²). В инструкции указывается, что каждое значение радиуса (скажем, от 500 до 1000 мм через каждые 2мм) следует умножить на самого себя и на π = 3,14, с занесением полученного результата в соответствующую графу таблицы.
К чему сводятся действия вычислителя? Прочитав в инструкции наименьшее значение радиуса (500), он устанавливает его на арифмометре, умножает сперва на точно такое же число, а потом на 3,14. Прочитав на арифмометре полученное произведение, вычислитель переносит его вместе со значением радиуса 500 в таблицу окончательных результатов.
Далее вычислитель должен прибавить 2 мм к прежнему значению радиуса, записать полученное новое (наращенное) значение радиуса в свой бланк и повторить с этим новым значением все ранее описанные действия. Когда в результате многократного повторения указанных операций он дойдет до значения радиуса 1002, превышающего установленный инструкцией верхний предел (1000), вычисления следует прекратить.
Как видим, собственно вычислений, т. е. арифметических действий над числами, человек не производит: они выполняются арифмометром. На долю вычислителя остается управление работой арифмометра, перенос числовых данных из инструкции или своего бланка на арифмометр и с арифмометра в таблицу результатов, а также «записывание» или, если угодно, «запоминание» необходимых промежуточных результатов. Чтобы полностью исключить участие человека из вычислительного процесса, нужно создать автомат, который самостоятельно выполнял бы все эти действия в соответствии с данной ему инструкцией.
Работа автомата по инструкции не таит в себе, конечно, ничего сверхъестественного или непостижимого. «Умеет» же аппаратура АТС безошибочно выполнять команды, которые мы посылаем ей набором телефонного номера. Нужно только, чтобы каждая команда была выражена на языке, доступном «пониманию» машины, например в виде определенной последовательности импульсов электрического тока.
Когда требуется длительная работа аппаратуры в соответствии с инструкцией, включающей множество команд, эту инструкцию следует тем или иным способом записать. Для хранения информации, выраженной электрическими импульсами, можно использовать, напри-
431
мер, магнитофон: комбинации электрических импульсов могут быть зафиксированы путем намагничивания участков магнитофонной ленты точно таким же способом, как это делают в звукозаписи. Впоследствии записанные команды, по мере их воспроизведения, будут управлять действиями автоматической аппаратуры. Записанную тем или иным способом инструкцию, которой должен «руководствоваться» автомат, принято называть программой.
На таких же магнитофонных лентах может быть записана не только инструкция, но и таблица исходных данных: ведь цифры, с которыми оперирует электронная вычислительная машина, тоже изображаются электрическими импульсами.
Первоначальный ввод в вычислительную машину исходных данных, а также команд программы может осуществляться с помощью специальной клавиатуры, вроде той, которая используется в телеграфных аппаратах: нажал клавишу - замкнулись контакты и по цепи побежала определенная комбинация импульсов электрического тока (в телеграфии она приводит в действие буквопечатающий аппарат, находящийся в другом городе, а в вычислительной машине намагничивает ленту магнитофона).
Электрические импульсы, выражающие окончательный результат вычислений, могут воздействовать на электромагниты печатающего аппарата (наподобие телеграфного), в результате чего мы получаем интересующие нас данные в форме обычной телеграммы.
Как видим, в современной технике нетрудно найти прообразы всех устройств, которые необходимы для полной автоматизации вычислительного процесса. Они нуждаются только в дальнейшем усовершенствовании для повышения их быстродействия и надежности.
Очень важно еще раз напомнить, что осмысливание и понимание выполняемых расчетов в обязанности вычислителя не входят: это дело «заказчика», который задумал расчет и воплотил весь свой замысел в инструкцию. Но, конечно, на практике внимательный и квалифицированный вычислитель не бывает вполне равнодушным к тому, что он делает; в частности, он может заметить и даже исправить грубые ошибки в инструкции, восполнить случайные пробелы, неясности и т. д.
В отличие от человека, от машины при решении ею задач нельзя, разумеется, ожидать никакой «сообразительности», основанной на понимании существа дела. Поэтому инструкция для машины должна быть составлена в такой форме, которая заранее исключала бы всякую двусмысленность, сомнения и необходимость руководствоваться здравым смыслом. Такого рода инструкция - свод четко сформулированных правил, применимых к достаточно широкому классу задач и всегда приводящих к определенному результату, в математике называется алгоритмом. Мы все изучали в средней школе алгоритм деления «уголком», алгоритм извлечения квадратного корня из многозначного числа и т. д., но только не пользовались таким «ученым» названием. Действие любой современной вычислительной машины состоит в том, что она с педантической точностью и аккуратностью выполняет последовательные предписания того или иного алгоритма, например алгоритма решения дифференциального уравнения или алгоритма перевода текста с английского языка на русский.
Категорический характер предписаний, которые составляют алгоритм, вовсе не означает, что вся последовательность действий машины во всех деталях заранее известна составителю данного алгоритма. Ведь категорическое предписание может иметь и такую форму: «Если в результате деления получится число меньше тысячи, увеличить его в два раза, а если получилось число не меньше тысячи - прибавить к нему восемьдесят три». Что будет делать машина фактически - умножать на 2 или прибавлять 83, этого составитель алгоритма заранее не знает, так как ему еще не известно, какое именно число получится при делении.
Про такой алгоритм говорят, что он предусматривает условный переход к выполнению той или иной последовательности операций в зависимости от результатов уже выполненных действий. Как мы увидим в дальнейшем, такие условные переходы играют огромную роль в работе электронных вычислительных машин, в значительной степени определяя их гибкость и возможность применения к решению весьма сложных математических и логических задач,
Быстродействующая электронная вычислительная машина состоит из пяти основных устройств: вводного, запоминающего, арифметического, выводного и управляющего (см. цветную вклейку на стр. 432-433). Кроме того, имеется дополнительное устройство для контроля работы и обнаружения неисправностей.
432
Вот как наш художник изобразил принцип действия электронной вычислительной машины.
Вводное устройство имеет обычно клавиатуру, посредством которой в машину вводятся исходные данные и задается определенная программа. Электрические импульсы, возникающие при нажатии на клавиши, направляются в запоминающее устройство. Возможны и иные конструкции устройства ввода (рис.6).
Запоминающее устройство (или «память» машины, как его иногда для краткости называют) предназначено для хранения информации: исходных данных числовых величин, команд программы, промежуточных и окончательных результатов. Оно играет роль памяти или записной книжки вычислителя.
Как уже было сказано, числовые данные могут записываться с помощью магнитофонов; но этот способ не самый совершенный, так как для воспроизведения ранее записанного числа может потребоваться длительная перемотка ленты. Поэтому разработаны другие способы «запоминания»: например, путем намагничивания ферритовых сердечников или же электризации отдельных участков диэлектрического экрана электронно-лучевой трубки.
Рис.6. Ввод данных, заранее пробитых на перфокартах.
Рис.7. Одно из выводных устройств.
Удобство последнего метода состоит в том, что для записи или воспроизведения числа электронный луч может быть направлен в нужную точку экрана практически мгновенно.
Носитель информации запоминающего устройства (магнитофонная лента, диэлектрический экран) состоит из множества «ячеек памяти», в каждой из которых может храниться одно многозначное число.
Каждой ячейке присвоен номер (наподобие телефонного); по этому номеру с ней можно в любой момент «соединиться», чтобы поместить туда или, наоборот, «истребовать» оттуда соответствующее число.
Арифметическое устройство служит для выполнения основных арифметических и некоторых логических действий. Оно содержит несколько электронных «арифмометров» (осуществляющих сложение, умножение и т. д.). Такие арифмометры чаще всего строятся на основе современных заменителей электронных ламп, что делает их более совершенными. В быстродействующих машинах каждая операция выполняется арифметическим устройством за десяток микросекунд.
433
Выводное устройство (рис.7) предназначено для выдачи заказчику готовой продукции в виде таблицы окончательных результатов произведенного расчета (рис.8) отпечатанной обычным шрифтом с помощью цифропечатного телеграфного аппарата под влиянием электрических импульсов, поступающих из запоминающего устройства. Для ускорения вывода результатов вместо печатания иногда применяют фотографирование их на кинопленку.
Управляющее устройство связывает воедино отдельные части вычислительной машины и «управляет», или «руководит», всем ходом вычислительного процесса; именно оно выполняет роль вычислителя. Во время работы машины управляющее устройство, действуя согласно программе, последовательно осуществляет все необходимые соединения и переключения, «отпирает» и «запирает» лампы, управляет движением электронных лучей и магнитофонных лент. Благодаря этому обеспечивается правильное размещение в ячейках памяти вводимых в машину исходных данных, своевременная передача чисел из определенных ячеек на те или иные «арифмометры» арифметического устройства, а также направление получающихся результатов в предназначенные для них ячейки. Наконец, по мере накопления * окончательных результатов в ячейках памяти управляющее устройство «соединяет» их с печатающими аппаратами.
Как видим, по своим функциям управляющее устройство вычислительной машины во многом напоминает автоматическую телефонную станцию, но оно должно делать сотни тысяч различных соединений в секунду! Кроме того, в отличие от АТС, управляющее устройство должно действовать не в соответствии с только что набранным номером, а по заранее заданной программе, которая (в зашифрованном виде) хранится в специально для этого отведенных ячейках памяти.
Программа работы электронной вычислительной машины для решения определенной задачи составляется специалистами и через вводное устройство «вводится» в машину перед началом вычислений.
Программа представляет собой последовательность отдельных «команд». Каждая команда состоит из указания определенного арифметического действия (сложение, вычитание, умножение и т. д.), номеров (или «адресов») тех ячеек памяти, откуда следует взять числа, над которыми должно быть произведено действие, а также номера (или «адреса») ячейки, куда должен быть помещен полученный результат.
Каждое арифметическое действие условно обозначается числом - «кодом», например: сложение - «1», вычитание - «2», умножение - «3» и т. д. Адреса ячеек памяти также обозначаются номерами, например: № 20, № 21, № 22 и т. д. В целом вся команда записывается в виде одного многозначного числа, в котором на первом месте стоит код действия, на втором и третьем местах - адреса чисел, над которыми надо совершать это действие, а на последнем (четвертом) месте - адрес ячейки, куда должен быть направлен полученный результат. Так, например, команда 3-21-26-52 предписывает перемножить числа, взятые из ячеек № 21 и 26, и поместить произведение в ячейку № 52. Такие команды называются трехадресными. Возможны команды и с иным числом адресов.
Поскольку команды управления машиной записываются многозначными числами, они наравне с другими числами могут быть помещены в ячейки запоминающего устройства: первая- в ячейку № 1, вторая - в ячейку № 2 и т. д.
Помимо арифметических, команды могут задавать машине и некоторые другие действия, например: «сравнить два числа», «отпечатать число, хранящееся, в такой-то ячейке памяти, в такую-то графу таблицы».
Составление программы и работа управляющего устройства. лучше всего разъясняются на каком-нибудь простеньком примере. Рассмотрим для этой цели составление таблицы значений площади круга, о которой мы уже говорили, описывая работу вычислителя.
Программа для выполнения соответствующих вычислений имеет такой вид:
Как видим, программа состоит всего из семи команд, которые перед началом работы при помощи вводного устройства размещают в ячей-
434
Рис.8. Решение на перфоленте и отпечатанное. В середине - оператор за пультом.
ки памяти с адресами от № 1 до 7. Помимо программы, в машину вводятся еще и необходимые исходные данные (рис.9): в ячейку № 20 - число p =3,14, в ячейку № 21 - наименьшее значение радиуса (500), с которого должна начинаться таблица, в ячейку № 22 - наибольшее значение радиуса (1000), в ячейку № 23 - число 2, показывающее, что значения радиуса надо брать через каждые 2 мм. Ячейка № 19 будет использоваться для записи в нее промежуточных результатов.
Рис.9. Размещение исходных данных.
После запуска машина будет выполнять команды в той последовательности, в какой они размещены в ячейках.
Согласно первой команде (3-21-21-19) начальное значение радиуса (500), хранящееся
в ячейке № 21, будет умножено само на себя, а полученное произведение (квадрат радиуса) помещено в свободную пока что ячейку № 19.
Согласно второй команде (3-19-20-19) это произведение (R²) будет умножено на число p, хранящееся в ячейке № 20, с помещением результата в ячейку № 19 (при этом ранее записанное там число автоматически стирается, подобно старой фонограмме при записи звука на магнитофоне).
Согласно третьей команде (7-21-00-01) значение радиуса из ячейки № 21 будет отпечатано печатающим аппаратом № 1, заполняющим первую графу таблицы.
Согласно четвертой команде (7-19-00-02) печатающим аппаратом № 2 во второй графе таблицы будет отпечатано соответствующее значение площади круга, взятое из ячейки № 19.
Последующие команды служат для перехода к вычислению площади круга для новых значений радиуса или для окончания работы, когда все требуемые значения уже исчерпаны.
Согласно пятой команде (1-21-23-21) к старому значению радиуса (500) прибавляется 2, причем полученный результат (новое значение радиуса 502) направляется в ту же ячейку
435
№ 21, где находилось прежнее значение радиуса.
Согласно шестой команде (8-21-22-01) производится сравнение двух чисел с адресами № 21 и 22. Если первое из них меньше второго или равно ему, то машина возвращается к выполнению команды № 1, указанной в третьем адресе, в противном же случае она просто переходит к выполнению следующей (очередной) команды. В нашем случае новое значение радиуса (из ячейки № 21) сравнивается с наибольшим его значением, для которого еще нужно вычислять площадь круга. Если новое значение радиуса не больше 1000, машина проделывает над ним те же самые вычисления, начиная с первой команды, и таким образом заполняет еще одну строку таблицы. Если же новое значение радиуса больше 1000, то машина переходит к выполнению седьмой команды, согласно которой она попросту останавливается с подачей на пульт управления сигнала об окончании вычислений.
В работе вычислительной машины команда сравнения <8> и другие подобные ей команды «условного перехода» имеют исключительное значение. Они увеличивают гибкость машины, расширяют ее возможности и позволяют выполнять действия, для которых она на первый взгляд вовсе не приспособлена.
Многократное повторение одной и той же последовательности действий позволяет производить длинные вычисления по сравнительно короткой программе (иначе ведь составление программы и введение ее в машину потребовало бы, пожалуй, не меньше времени, чем вычисления вручную). Еще эффективнее другой прием сокращения программы, который состоит в систематической переработке ее в процессе самих вычислений. Ведь все команды программы изображаются числами, хранящимися в запоминающем устройстве на равных правах с исходными данными и промежуточными результатами. Ничто не мешает нам производить над этими числами арифметические действия и тем самым превращать одни команды в другие. Конечно, все эти преобразования команд на определенном этапе вычислений или при получении определенных результатов должны быть заранее предусмотрены самой программой (подобно тому, как устав всякой общественной организации в числе других правил содержит обычно также и правила изменения самого устава).
Допустим, что значения площади круга нужно определить только для некоторых ранее
вычисленных значений радиуса - скажем, записанных в ячейках памяти № 21-80 (рис.10). Тогда, как и прежде, в ячейку № 20 помещаем p, а в ячейки № 81 и 82 - специальные числа 0-01-01-00 и 3-80-80-19, значение которых выяснится в дальнейшем. Вычисления будем вести по следующей программе:
По первой команде вычисляется квадрат первого значения радиуса (из ячейки № 21), который затем по второй команде умножается на p. По третьей команде вычисленное значение площади круга заносится в таблицу окончательных результатов.
Теперь нужно повторить те же самые операции, но уже над новым значением радиуса, хранящимся не в 21-й, а в 22-й ячейке. Для этого можно было бы включить в программу в качестве четвертой команды 3-22-22-19 (возвести новое значение радиуса в квадрат) с последующим повторением второй и третьей команд без изменения. Затем должна следовать команда 3-23-23-19 (возвести в квадрат значение радиуса из ячейки № 23) и т. д.
При большом количестве различных значений радиуса программа получалась бы очень громоздкой. Легко сообразить, что вводимые вновь команды 3-22-22-19, 3-23-23-19,... могут быть получены из первой команды 3-21-21-19
436
последовательным прибавлением к ней числа 0-01-01-00, хранящегося в ячейке № 81:
Таким образом, посредством арифметических действий над числом, изображающим команду, может быть осуществлено систематическое изменение ее адресов (в данном случае первого и второго), а если потребуется, то и кода действия. Такая операция изменения адреса (называемая переадресацией) как раз и осуществляется по четвертой команде рассматриваемой программы. При этом число, изображающее новую (переадресованную) команду, направляется в ту же ячейку № 1, где хранилась исходная команда (в случае надобности переадресованную команду можно было бы поместить и в другую ячейку памяти).
По пятой команде выполняется сравнение переадресованной команды (числа) из ячейки № 1 с командой 3-80-80-19, специально введенной для этого в ячейку № 82. Пока первый и второй адреса переадресованной команды не больше 80 (использованы еще не все значения радиуса, хранящиеся в ячейках № 21- 80), согласно команде сравнения осуществляется возврат к началу программы, т. е. к исполнению переадресованной первой команды. Когда же все значения радиуса будут исчерпаны, команда примет вид 3-81-81-19, т. е. превзойдет число в ячейке № 82, и по команде сравнения машина перейдет к выполнению следующей (шестой) команды, означающей остановку.
Как уже было сказано, преобразование программы в ходе ее выполнения, наряду с периодическим повторением ее частей и другими приемами, неизмеримо расширяет возможности вычислительной машины, позволяя решать на ней даже сложнейшие задачи высшей математики, хотя арифметическое устройство машины способно выполнять только четыре арифметических действия да несколько простейших логических операций.
Секрет современной вычислительной машины заключается не в ее элементах, какими бы чудесными они ни представлялись, а в их очень гибкой и сложной взаимосвязи, которая молниеносно меняется в соответствии с заданной
программой. Вводя в одну и ту же машину различные программы, можно заставить ее решать самые разнообразные задачи из очень далеких друг от друга областей умственного труда. В зависимости от программы одна и та же машина способна вычислять траекторию космического корабля, предсказывать погоду, играть в шахматы, управлять работой железнодорожного узла и переводить книги с английского языка на русский. Именно это и делает электронную машину универсальным средством автоматизации умственного труда, без применения которого столь характерные для нашей эпохи стремительные темпы научно-технического прогресса были бы невозможны.
Благодаря применению электронных машин удается отделить творческий процесс нахождения общих принципов решения той или иной проблемы от кропотливого и механического осуществления этих принципов. Чем большая доля механической умственной работы возложена будет на машины, тем больше времени и сил сможет уделить исследователь действительно научному творчеству.
Как выяснилось, составление программ вычислений тоже заключает в себе немалую долю формальных, механических операций. Составитель программы должен не только придумать общий план (или логическую схему) решения задачи (что является актом творчества), но также и кропотливо расписать во всех подробностях все последовательные шаги машины (для чего достаточно лишь с педантической аккуратностью придерживаться определенных правил). Для ускорения естественно разделить эти две различные по своему характеру задачи: творческий поиск логической схемы оставить за человеком, а механическую работу детального расписывания команд возложить на саму электронную машину. Для этой цели составлены так называемые программирующие программы, на основе которых сама вычислительная машина автоматически преобразует введенную в нее человеком логическую схему в детально разработанную программу. Тем самым объем работы программиста сокращается в десятки раз.
Логическая схема программы записывается человеком не в виде последовательности знакомых уже нам «команд», а на более привычном и лаконичном «языке» математической символики, т. е. посредством обычных формул лишь немного измененного начертания с отдельными дополнительными пояснениями. При отсутствии у машины специальной клавиатуры для
437
ввода математических символов и букв каждый из этих знаков предварительно кодируется числом вручную.
В настоящее время ведется большая работа по созданию универсального языка программирования, посредством которого каждый мог бы (после самого краткого обучения) самостоятельно писать логические схемы программ, вполне пригодные для непосредственного введения их в машину (снабженную раз и навсегда установленной программирующей программой). Это позволило бы вообще исключить малопроизводительный процесс программирования вручную. Один из вариантов такого универсального языка известен под условным названием «алгол».
Другой широко применяемый уже метод экономии труда и времени при программировании состоит в использовании библиотеки стандартных подпрограмм. В такой библиотеке хранятся составленные заранее программы для самых различных вычислений, встречающихся на практике. В числе их может быть, например, решение кубического уравнения или вычисление определенного интеграла. Когда такого рода вычисление встретится при решении конкретной задачи, машина сама «выпишет» из библиотеки необходимую для этого последовательность команд - достаточно только одного лаконичного упоминания об этом в соответствующем месте основной программы решения рассматриваемой задачи.
Такой метод тоже значительно повышает производительность труда при программировании.
Без далеко идущей автоматизации программирования решение очень многих, и притом весьма важных, задач на электронных машинах было бы практически невозможным, так как составление соответствующих программ потребовало бы чересчур много времени.
Универсальность электронных вычислительных машин свидетельствует о том, что даже самые несхожие между собой виды умственного труда могут быть разложены на одни и те же элементарные шаги, но только расположенные в иной последовательности и выполняемые над другим исходным материалом. Именно это обстоятельство делает возможным единый подход к проблеме автоматизации всех видов умственного труда. Изучение тех общих закономерностей автоматизации умственного труда, которые не зависят от конкретных особенностей различных его видов, составляет одну из очень важных и интересных задач
молодой науки кибернетики (см. статью «Что такое кибернетика?»).
Чтобы наглядно показать универсальность электронной вычислительной машины и единство резко различных по своему характеру видов умственного труда, попробуем хотя бы вкратце пояснить, каким образом «умудряется» машина переводить книги с одного языка на другой.
Английский текст для перевода вводится в запоминающее устройство, причем каждая буква изображается определенной комбинацией электрических импульсов. Кроме того, в память машины записываются словарь, грамматические таблицы и программа автоматического перевода.
Прежде всего машина отыскивает в словаре для каждого английского слова его русский эквивалент. Для нее это ничуть не сложнее, чем отыскать в тригонометрической таблице для заданного угла значение его косинуса. Но очень значительные трудности возникают при этом всякий раз, когда одно и то же английское слово, подобно, например, русскому слову «коса» (рис.11), имеет несколько различных значений. Переводчик обычно выбирает одно из этих значений, наиболее подходящее по смыслу, машина же может руководствоваться только формальными правилами, которые должны быть ей заранее заданы. Поэтому для всякого
Рис.11. Что значит «коса»?
438
многозначного слова в машинном словаре дается не перевод, а команда-ссылка - проанализировать это слово по специальной программке. Программка эта представляет собой последовательность вопросов, ответы на которые позволяют раскрыть смысл слова. Покажем, как это делается, на примере английского слова many.
Когда в предложении встречается это слово, машина его сначала пропускает и переводит все остальные. Но затем она обязательно возвращается к слову many и приступает к последовательному исполнению команд программки его анализа (рис.12).
Рис.12. Анализ слова many.
Первая команда этой программки гласит: проверить предыдущее слово, не является ли оно словом how. Если да - машина дает перевод «сколько», потому что сочетание how many всегда имеет именно такое значение.
Если же нет - машина переходит к следующей проверке: не является ли предыдущее слово словом as.
Если да - перевод будет «столько же», потому что таков смысл сочетания as many.
Если нет - машина должна проверить, не является ли предыдущее слово предлогом, а последующее - существительным.
Такая проверка легко осуществима, так как большинство слов предложения уже переведено, а перевод содержит все необходимые грамматические сведения, выписываемые вместе с самими словами из словаря.
При положительном ответе (да) машина должна будет записать перевод «многий», при отрицательном (нет) - «много». Особенно существенно здесь то, что в первом случае слово «многий» - это прилагательное с мягким окончанием, а во втором («много») - неизменяемое наречие.
Когда все переводы для всех (в том числе и многозначных) слов найдены и зафиксированы в запоминающем устройстве, машина начинает оформлять их в соответствии с правилами; русской грамматики.
В частности, прилагательное «многий» должно быть поставлено в нужном падеже, роде и числе. Род, падеж и число прилагательного обычно определяются тем русским существительным, перед которым оно стоит. В свою очередь род русского существительного при переводе был выписан из словаря, число определено по окончанию английского слова, а падеж выяснен при анализе по предыдущему предлогу или глаголу.
На основании этих данных машина заменяет в слове «многий» окончание «-ий» другим, которое берется из грамматических таблиц для прилагательных с мягкими окончаниями (такие таблицы, как и словарь, тоже хранятся в машинной памяти). Следующий этап вклю-
1. Забавный вид имеют записи действий, выполненных в других - недесятичных - системах счисления. Например,
а) 31-13 = 13;
б) 2×2 = 10;
в) дана дробь 16 ⁄ 61, сокращая на 7, получим
| 16 61 | = | 2 7 | ; |
В какой системе счисления выполнялось каждое действие, если все результаты правильные?
2. (3 ⁄ 7)10 = (11 ⁄ 111)2 = 0,011011. Как это получается?
3. Докажите, что для записи одного миллиарда в двоичной системе надо употребить 30 цифр.
Решение на стр.500.
439
Электронный «закройщик» - цифровая вычислительная машина «Сталь-1», установленная на одном из металлургических комбинатов страны. Она мгновенно замеряет длину полосы металла, составляет план ее раскроя и подает команду ножницам. Вся операция занимает полсекунды. Кроме того, «Сталь-1» непрерывно регистрирует вес прокатных заготовок.
чает в себя обработку перевода по правилам синтаксиса и определение порядка слова.
После того как синтез русского предложения закончен, перевод передается в выводное устройство, которое и печатает его русскими буквами на бумаге (если какого-нибудь английского слова машина в своем словаре не нашла, она впечатывает его в текст перевода латинскими буквами).
Пока что автоматический перевод книг практического применения не нашел - нужна еще большая предварительная работа, которая может быть выполнена только совместными усилиями филологов, математиков и инженеров. Однако успех даже первых, пускай еще примитивных опытов в этом направлении еще раз подтверждает, что область применения электронных вычислительных машин не ограничивается одними только математическими вычислениями.
Электронные вычислительные машины должны быть, без всякого сомнения, отнесены к числу наиважнейших факторов научно-технического прогресса.
440
Одно из важных понятий, которым оперирует современная наука,- понятие управляющей системы. С разнообразными управляющими системами мы встречаемся в технике, в растительном и животном мире, а также в человеческом обществе.
Простейший пример технической управляющей системы - примитивный поплавочный регулятор уровня воды, изображенный на рис.1. Задача этого регулятора - поддерживать постоянный уровень жидкости в сосуде. Регуляторы подобного типа употребляются в простейших паровых котлах.
Жидкость может выливаться из сосуда по трубе F и поступать в сосуд по трубе АВ. В жидкость помещен поплавок Н, закрепленный на рычаге СЕ. При повышении уровня жидкости в сосуде поплавок всплывает, а рычаг СЕ, поворачиваясь на оси С, специальной пробкой D закрывает конец трубы В. При понижении уровня жидкости пробка D опускается и открывает доступ жидкости в сосуд по трубе АВ до тех пор, пока не будет восстановлен исходный уровень.
В рассмотренном примере управляющая система состоит из поплавка Н, рычага СЕ и пробки D. Эта простейшая система заключает в себе все основные черты гораздо более сложных управляющих систем. Действительно, любая управляющая система должна иметь прежде всего чувствительный элемент (вводное устройство), с помощью которого она воспринимает сведения, или, как обычно принято говорить, информацию о состоянии объекта управления (в данном случае - сосуда с жидкостью). В нашем примере таким чувствительным элементом служит поплавок.
Далее, управляющая система должна содержать устройство, преобразующее информацию,
полученную от объекта управления с помощью чувствительного элемента. Подобным преобразователем информации может считаться рычаг СЕ.
Наконец, управляющая система должна иметь возможность воздействовать на объект управления с помощью того или иного исполнительного механизма (выводного устройства). В нашем примере таким механизмом служит пробка D, закрывающая конец трубы В.
В современной технике мы встречаемся с автоматическими системами, несравненно более сложными, чем описанный простейший автоматический регулятор. Еще более сложны многие биологические управляющие системы. Первое место среди них занимает нервная система человека, особенно его головной мозг. Подобно техническим управляющим системам, нервная система человека также обладает чувствительными элементами (окончания нервов в органах чувств), исполнительным механизмом (окончания нервов, управляющих мышцами) и преобразователем информации (собственно нервная система). Такую же схему строения имеют и другие биологические управляющие системы.
А как устроены различные управляющие системы в человеческом обществе? Возьмем, например, систему управления экономикой. Чувствительный элемент ее - аппарат первичного учета, собирающий различные сведения о состоянии народного хозяйства. Преобразование собранной информации и выработка соответствующих решений осуществляются в Госплане, совнархозах и т. п. Имеется также и специальный исполнительный аппарат на предприятиях, проводящий в жизнь принятые решения.
Все приведенные примеры показывают, что, несмотря на принципиальные различия, существующие в рассмотренных управляющих системах, они имеют нечто общее. Изучение общих законов функционирования различных управляющих систем составляет предмет специальной науки - кибернетики.
Термин «кибернетика» происходит от древнегреческого слова «кибернетес» - рулевой и напоминает, что кибернетика представляет собой науку об управлении, или, более точно, науку об общих законах преобразования информации в управляющих системах.
Этот термин впервые употребил в 1834 г. французский физик А. Ампер, назвав кибернетикой не существовавшую еще в то время науку об управлении обществом. В 1948 г.
441
американский ученый Н. Винер словом «кибернетика» назвал общую науку об управлении.
В настоящее время кибернетика является теоретической основой автоматизации, причем главным образом автоматизации многих видов умственной деятельности человека.
Следует подчеркнуть еще раз, что кибернетика изучает общие законы управляющих систем. Но между техническими и биологическими системами или, тем более, между ними обеими и управляющими системами в человеческом обществе имеются глубокие качественные различия. Поэтому наряду с кибернетикой существуют науки, изучающие особенности управляющих систем различных типов. К ним относятся техническая автоматика, физиология нервной системы и большая группа социальных (общественных) наук.
Сама кибернетика также делится на ряд разделов, многие из которых (подобно алгебре или геометрии внутри математики) выросли уже в самостоятельные науки.
Важная составная часть кибернетики - так называемая теория информации. Она изучает различные формы представления и передачи информации как в отвлеченном (абстрактном) виде, так и применительно к конкретным управляющим системам. Информация может представляться в двух различных формах - непрерывной и дискретной (т. е. прерывистой).
В первом случае информация представляется в виде плавно, непрерывно меняющихся величин. Например, при передаче речи по радио или по телефону звуки речи представляются в виде плавно изменяющихся электрических величин - напряжения или тока. При передаче той же речи по телеграфу с помощью азбуки Морзе или при записи ее на бумаге характер представления меняется, информация разбивается на отдельные порции: точка и тире, буквы русского или какого-нибудь другого алфавита; переходы от одной порции к другой совершаются скачками. Это уже дискретная форма представления информации.
На современном уровне развития кибернетики особо важное значение приобрела дискретная форма представления информации. Оказывается, что информация, заданная в непрерывной форме, может быть с любой наперед заданной точностью представлена в дискретной
форме. Более того, в качестве отдельных порций, на которые разбивается эта дискретная информация, может быть выбрано любое наперед заданное множество каких-либо значков (обобщенных букв), называемое обычно абстрактным алфавитом. Важно лишь, чтобы этот алфавит содержал более одной обобщенной буквы. Процесс представления информации последовательно расположенными буквами того или иного абстрактного алфавита называется кодированием.
Для примера рассмотрим процесс кодирования в абстрактном алфавите информации, заданной с помощью рис.2. Абстрактный алфавит состоит из двух обобщенных букв - О и 1. Для этой цели разобьем рисунок на прямоугольнички, размеры которых зависят от того, с какой точностью мы хотим представить информацию.
Условимся обозначать каждый прямоугольничек нулем, если более половины его площади не зачернено, и единицей в противном случае.
Тогда, пробегая все прямоугольнички по строкам слева направо, а строки сверху вниз, мы получим для рис.2 следующий дискретный код: 00000000011001100000. Разумеется, такое представление описывает рисунок с малой точностью. Однако, уменьшая размеры прямоугольничков, мы можем добиться сколь угодно высокой точности описания.
В теории информации разработаны не только способы кодирования различных сообщений, но и способы количественной оценки содержащейся в них информации.
Вопросы кодирования и декодирования, т.е. восстановления исходного вида информации по ее дискретному коду, и другие проблемы возникают в первую очередь при разработке вводных и выводных устройств управляющих систем. Теоретическую основу устройств для преобразования информации составляют другие
442
разделы современной кибернетики - теория алгоритмов и теория автоматов.
Алгоритмом называется конечная система правил, по которым совершается преобразование дискретной информации. Множество разнообразных алгоритмов имеется в математике. Из школьного курса алгебры, например, вам хорошо известны алгоритмы для решения квадратных уравнений, систем линейных уравнений, для раскрытия скобок и приведения подобных членов в буквенных выражениях и т. п. Но алгоритмы широко распространены и за пределами математики. Если сформулировать все правила, которые употребляет опытный переводчик для переводов, скажем, с английского языка на русский, то получим не что иное, как алгоритм англо-русского перевода.
Если элементарные правила шахматной игры дополнить системой стратегических правил, позволяющих в каждой позиции находить единственный, наилучший (с точки зрения данной системы правил) ход, то получится алгоритм игры в шахматы.
Оказывается, чуть ли не всякий вид умственной деятельности человека может быть сведен к выполнению того или иного алгоритма. Но практически найти все правила, составляющие эти алгоритмы,- часто очень сложная и трудоемкая задача.
Для кибернетики особенно важны два результата, полученные в теории алгоритмов. Первый результат - универсальность алгоритмических систем. Оказывается, для построения любого алгоритма достаточно уметь выполнять относительно небольшое число типов элементарных алгоритмических операций. Подобно тому как из одних и тех же элементарных частиц складываются молекулы самых различных веществ или как из одних и тех же букв складываются книги совершенно различного содержания, так и всякий алгоритм, независимо от его природы, можно составить в результате соответствующего комбинирования элементарных алгоритмических операций.
Второй важный результат теории алгоритмов заключается в том, что существуют так называемые алгоритмически неразрешимые проблемы, т. е. такие классы задач, которые для своего решения требуют бесконечного числа различных приемов. А всякий алгоритм обязательно включает в себя лишь конечное число приемов, хотя, может быть, и очень большое.
Так, например, можно построить алгоритм, который позволяет доказать любую теорему
из элементарной геометрии (не использующей понятие предела). В то же время доказано, что для теории чисел (устанавливающей различные свойства целых чисел) подобного алгоритма не существует. Иначе говоря, для построения элементарной геометрии достаточно конечного числа приемов (методов доказательства), а для построения теории чисел число соответствующих приемов должно быть непременно бесконечным.
Значение этих результатов для кибернетики становится ясным при переходе от теории алгоритмов к теории автоматов. Основная задача теории автоматов - разработка методов построения преобразователей информации для реализации тех или иных алгоритмов, например машин для игры в шахматы, для автоматического перевода с одного языка на другой и т. п.
Если существуют универсальные алгоритмические системы, то возможно в принципе построить универсальные преобразователи информации, способные реализовать любые алгоритмы. Подобные универсальные преобразователи уже построены и успешно работают. Это так называемые универсальные электронные цифровые машины. Цифровыми или вычислительными эти машины называются потому, что первым их назначением была реализация вычислительных алгоритмов. Информация, с которой они имели дело, была цифровой, т. е. набором чисел. Такие машины снабжаются так называемыми запоминающими устройствами (памятью), позволяющими им «запоминать» как перерабатываемую информацию, так и программу работы машины, т. е. записанный в условных кодах, называемых приказами, алгоритм, который должна реализовать машина.
Изменение программы происходит без каких-либо переделок машины. Достаточно пропустить сквозь машину набор бумажных карточек с пробитыми на них в соответствующих местах отверстиями - перфокарты или ленту с отверстиями - перфоленту. Так вводится в машину новая программа, настраивающая ее на совершенно новый вид работы.
Благодаря этому открываются широкие возможности для автоматизации различных
443
видов умственной деятельности человека. Достаточно найти алгоритм, описывающий тот или иной вид подобной деятельности, перевести его в программу, или, как говорят, запрограммировать, и ввести в машину.
На такой универсальной машине можно программировать любой алгоритм. Поскольку машина работает гораздо быстрее и точнее человека, она, как правило, выполняет заданный алгоритм гораздо лучше его. Отсюда понятно, какое большое практическое значение имеет кибернетика в автоматизации таких видов умственной деятельности, где человек уже сейчас не в силах справиться с переработкой информации за разумное время, например в научных и инженерных расчетах.
Во многих разделах современной науки и техники, таких, как атомная физика и ракетная техника, решаются задачи, требующие вычислений, состоящих из многих миллиардов арифметических операций. Даже при помощи специальных клавишных вычислительных приборов человек успевает в среднем выполнять за минуту лишь две арифметические операции над многозначными числами. А для выполнения одного миллиарда операций потребовалась бы тысяча лет непрерывной работы без сна и отдыха! В то же время современная электронная цифровая машина, выполняющая 500 тыс. арифметических операций в секунду, справится с этой работой немногим более чем за полчаса! При таком росте производительности труда становится возможным решать задачи, которые ранее были просто недоступны человеку.
Автоматизация расчетов требуется не только в новейших областях науки и техники. Так, в метеорологии только благодаря автоматизации удается выполнять к требуемому сроку сложные расчеты, необходимые для уточнения прогнозов погоды. В техническом проектировании внедрение автоматизации позволяет перейти от выбора лучших проектов из относительно небольшого числа вариантов к выбору наилучшего из всех возможных вариантов (так называемого оптимального проекта).
Рассмотрим, например, задачу выбора наилучшего варианта проекта железной дороги по заданному маршруту (трассе). Производя мысленный вертикальный разрез местности вдоль трассы, получим некоторую кривую, изображающую неровности рельефа (рис.3). Проложить дорогу непосредственно по этому рельефу, как правило, нельзя: подъемы и спуски получатся слишком крутыми, и преодолеть их при эксплуатации уже построенной дороги
либо окажется вовсе невозможно, либо потребуются слишком большие затраты (снижение скорости и веса составов, использование нескольких локомотивов и т. д.).
Необходимо поэтому проделать земляные работы, чтобы выровнять рельеф. Такое выравнивание проводят по нескольким выбранным отметкам (точки А, В, С, D, Е). Предположим, что таких точек всего 5, а каждая точка, за исключением крайних точек А и Е, находящихся на определенном уровне, может занимать 100 различных положений по высоте. В таком случае у нас будет 100³ =1 000 000 различных вариантов выравнивания рельефа.
Если просматривать их со скоростью два варианта в минуту, потребуется целый год. Если же число точек увеличивается до 100, то количество вариантов выражается единицей с 196 нулями, а количество лет, необходимое для их просмотра, - единицей со 190 нулями. В этом случае просмотреть все варианты практически невозможно не только для человека, но и для электронных вычислительных машин.
Необходимо поэтому разработать методы, позволяющие резко уменьшить количество просматриваемых вариантов, отбросить целые группы заведомо плохих. Разработкой такого рода методов занимается специальный раздел кибернетики - теория оптимальных решений.
В настоящее время разработан ряд методов для решения задач оптимального проектирования, планирования и управления. Многие из этих методов были предложены и обоснованы советскими учеными (метод линейного программирования Л. В. Канторовича, принцип максимума Л. С. Понтрягина и др.). Для решения задач оптимального проектирования дорог, линий электропередач и др. удобен метод последовательного анализа вариантов, разработанный в Институте кибернетики АН УССР. С помощью этого метода оптимальный вариант выравнивания рельефа для прокладки железной дороги в несколько сотен километров находится вычислительной машиной среднего быстродействия (10-20 тыс. операций в секунду) за 2-3 часа.
В ряде областей техники разрабатываются системы алгоритмов, позволяющие осуществить
444
полную автоматизацию проектирования многих сложных объектов.
Не менее важно также оптимальное планирование и управление народным хозяйством. Эти вопросы выделяют обычно в специальный раздел кибернетики - экономическую кибернетику. Масштабы производства и темпы роста народного хозяйства в СССР так велики, что обычные, неавтоматизированные методы планирования уже не могут нас удовлетворить. Практика показывает, что выбор оптимальных (наилучших) вариантов планов уже сейчас практически недоступен никакому человеческому коллективу, не пользующемуся электронными цифровыми машинами.
Электронные цифровые машины используются пока для решения лишь частных планово-экономических задач. Особенно успешно решаются так называемые транспортные задачи (нахождение планов перевозок с минимальными транспортными расходами), а также задачи о наилучшей загрузке станков и другие, решающиеся с помощью методов линейного программирования. Экономия, получаемая при такой автоматизации, исчисляется обычно 10-15%, а в отдельных случаях доходит до 50-60%.
На повестке дня сейчас полная автоматизация не только самих процессов планирования и управления экономикой, но и процессов сбора необходимой первичной информации, автоматизация учета и справочно-статистической работы. С этой целью создаются специальные вычислительные центры, снабженные мощными электронными цифровыми машинами и соединенные между собой, а также с производством современными каналами связи для быстрой передачи необходимой информации.
К задаче оптимального управления экономикой тесно примыкает задача оптимального управления производственными процессами. Сейчас еще во многих случаях диспетчер или группа диспетчеров управляет тем или иным сложным процессом далеко не лучшим образом. Дело в том, что человеческий мозг не успевает своевременно перерабатывать огромный объем необходимой информации. Помочь здесь могут только автоматические управляющие системы, среди которых надо особо выделить специально приспособленные для управления универсальные электронные цифровые машины.
Эти машины, называемые обычно универсальными управляющими машинами, снабжаются особыми вводными и выводными устройствами, позволяющими автоматически собирать и выдавать информацию, необходимую для управления производством.
ЭЦВМ «Урал-2». Внешний вид центральной части.
Одна из первых универсальных управляющих машин, разработанная в Киеве, изображена на рис.4. Такая машина успешно управляет процессом выплавки стали, газорезательным станком и рядом других различных процессов.
Для управления производственными процессами на значительных расстояниях можно использовать стационарные электронные цифровые машины, установленные в вычислительных центрах. Такие опыты успешно проводи-
445
Конвертер для выплавки стали управляется машиной УМШН.
Варианты рациональных перевозок, рассчитанные машиной.
лись в США, а также в СССР (Институт кибернетики в Киеве).
Но создание технической базы, т. е. управляющих машин, лишь наполовину решает проблему автоматизированного управления производственными процессами. Не менее важно решить задачу алгоритмизации, т. е. найти эффективные алгоритмы для управления производственными процессами. Построением общей теории управления техническими (производственными) объектами занимается техническая кибернетика.
Алгоритмизация производственных процессов обычно чрезвычайно трудоемка, а из-за непрерывного совершенствования технологии
446
необходимо часто изменять и совершенствовать алгоритмы управления, Поэтому все чаще стараются использовать такие системы, которые могут самосовершенствоваться.
Обычно самосовершенствование осуществляется следующим образом. Помимо собственно управляющего алгоритма, так называемого рабочего алгоритма или алгоритма первой ступени, вводится еще один - алгоритм второй ступени. Он контролирует результаты работы первого алгоритма и изменяет некоторые части этого алгоритма с целью улучшения этих результатов. Применение универсальных электронных цифровых машин с самосовершенствующейся системой алгоритмов обеспечивает, как правило, более высокое качество управления. В настоящее время обычно применяют двухступенчатые самосовершенствующиеся системы, о которых мы говорили. Однако возможно построить и более сложные, многоступенчатые системы.
Особенно велико значение самосовершенствующихся систем при решении одной из самых увлекательных задач кибернетики - задачи моделирования процессов, протекающих в мозгу человека. Дело в том, что человеческий мозг - очень сложная и во многих отношениях замечательно устроенная самосовершенствующаяся система. Возможности мозга можно наглядно проиллюстрировать таким примером. Человек внешне относительно просто приспособляется к распознаванию какого-либо класса изображений, например рисунков, изображающих различные дома. Если показать человеку сравнительно небольшое число изображений домов, например одноэтажных и пятиэтажных, он может правильно классифицировать и изображение, которое ему никогда ранее не было показано, например, двухэтажных, трехэтажных и других домов. Значит, можно выработать у человека достаточно правильное представление об общем понятии дома.
Для моделирования способности мозга приспосабливаться к распознаванию различных классов изображений в кибернетике было построено большое число различных алгоритмов и проведено большое число экспериментов. Эти эксперименты пролили свет на многие процессы, происходящие в мозгу, и послужили в ряде случаев основой для решения практических задач по автоматизации процессов рас-
познавания зрительных образов, а также человеческой речи. Впрочем, в направлении автоматического распознавания речи сделаны пока еще лишь первые шаги; машина распознает всего несколько десятков различных слов, произносимых различными голосами в различных условиях.
Обучение машин процессам распознавания зрительных и других образов - лишь самая первая, относительно несложная задача в моделировании мыслительных процессов. Более сложные задачи возникают при моделировании логического мышления, процесса обучения языку, при моделировании процессов творчества.
В области логического мышления в первую очередь моделируются различные системы, позволяющие осуществлять автоматическое доказательство теорем в тех или иных (пока еще достаточно узких) областях математики. При этом речь идет об автоматическом доказательстве не только теорем, вошедших в учебники, но и новых, еще не известных человеку теорем. Значение такой автоматизации огромно: используя скорость и безошибочность работы даже современных, относительно еще мало совершенных, универсальных электронных цифровых машин, очевидно, можно будет в ближайшем будущем доказывать такие сложные теоремы, которые «невооруженному» человеческому уму просто недоступны.
Здесь кибернетика начинает вплотную подходить к внедрению автоматизации в развитие самой науки. В будущем кибернетические машины будут незаменимыми помощниками человека не только в доказательстве новых теорем, но и в обобщении результатов наблюдений, в построении новых физических и других теорий и т. д. Уже сейчас, помимо помощи в сложных вычислениях и обработке экспериментальных данных, машины начинают применяться для автоматизации справочно-информационной и библиографической работы, отнимающей сейчас много времени у ученых. В принципе возможно накапливать научную информацию не только в библиотеках, но и в электронной памяти кибернетических машин в специальных информационных центрах. Из этих центров по запросу того или иного ученого может быть очень быстро получена необходимая справка, краткое или полное содержание какой-либо научной статьи и т. п.
Важное место в автоматизации научного творчества займут также автоматический перевод с одного языка на другой, автоматическое
447
ЭЦВМ «Пром i нь».
реферирование и конспектирование статей и т. п. Для этих целей в машину должна быть вложена та или иная система знаний о человеческих языках. На первых порах в эту систему включаются обычно лишь необходимый словарный запас и грамматические правила. Однако в принципе ничто не препятствует тому, чтобы обучать машины распознаванию смысла вводимых в нее фраз.
Опыты такого рода были проделаны в Академии наук УССР. Во время этих опытов универсальная электронная цифровая машина, работая в специальном режиме (так называемом режиме обучения), обучалась отличать осмысленные фразы, составленные из выбранных наугад 100 слов, от бессмысленных. Важно подчеркнуть, что процесс обучения был организован таким образом, что машина не просто «зазубривала» вводимые в нее «учителем» фразы, а создавала новые понятия, задавала учителю вопросы и, будучи переведена в режим экзамена, правильно различала осмысленность не только тех фраз, которые ей были сообщены «учителем», а также и новых, которые ей раньше никогда не сообщались.
Формула, которую считали на ЭЦВМ «Пром i нь».
Результаты решения формулы на машине «Пром i нь» .
Отсюда возникает очень актуальный и острый вопрос: возможна ли автоматизация процессов творчества? Что касается научного творчества, об этом уже говорилось выше. Необходимо лишь ответить на вопрос о том, в какой мере ответы машины предопределяются заложенной в нее программой. Не потребуется ли программисту затратить больше усилий на составление программы, чем на непосредственное
решение вопроса, заключенного в данной программе?
Чтобы ответить на этот вопрос, рассмотрим простой пример. Предположим, что программист не знает, каким образом решаются квадратные уравнения, но может проверить, является ли то или иное число корнем заданного квадратного уравнения. В таком случае он без особых затруднений может составить программу, по которой машина будет пытаться решать квадратные уравнения по различным формулам, последовательно перебирая все такие формулы - от более простых к более сложным. При этом каждая такая попытка будет проверяться с помощью подстановки определяемых по испытуемой формуле корней в заданное уравнение (или в несколько заданных уравнений). В случае неудачи машина должна автоматически строить следующую формулу и испытывать ее - и так до тех пор, пока очередная попытка не приведет к успеху. Благодаря огромной скорости работы машины она довольно скоро найдет требуемую формулу.
Для решения более сложных проблем применение метода такого простого перебора может не привести к успеху даже при использовании машин. Однако, как правило, благодаря огромной быстроте действий машина может решать соответствующие проблемы с помощью более простых методов, чем те, которые потребовались бы для этой цели человеку. Поэтому составление программы для решения даже единичной проблемы творческого характера может оказаться более простым делом, чем непосредственное решение самой проблемы. В действи-
448
ЭЦВМ «Киев».
ЭЦВМ «Киев». Экран визуального вывода информации.
Результаты решения формулы на машине.
тельности же положение облегчается еще и тем, что составленная программа используется для решения большого числа проблем одного типа.
Возможности автоматизации творческих процессов не ограничиваются рамками одних лишь точных наук. Уже сейчас, когда кибернетика делает только первые робкие шаги, проведены успешные опыты по автоматизации музыкального творчества; машины сочиняют стихи (правда, пока еще плохие), играют в шахматы и т. д. С каждым днем перед автоматизацией процессов творчества открываются все новые и новые горизонты. Однако, разумеется, далеко не во всех областях подобная автоматизация так необходима, как в процессах научного творчества.
Вряд ли сегодня практически необходимо автоматизировать литературное или музыкальное творчество. Вместе с тем кибернетика уже сегодня начинает приносить пользу, скажем, поэзии, внося в нее точные математические методы исследования.
Особый интерес представляют взаимосвязи, существующие между кибернетикой и биологией. Кибернетика дает в руки биологам новые методы исследований. Универсальные электронные цифровые машины позволяют моделировать процессы эволюции и естественного отбора, автоматизировать процесс определения болезней по их признакам, осуществлять моделирование механизма возникновения условных рефлексов и других видов деятельности мозга животных и даже мозга человека.
Биология в свою очередь снабжает кибернетику новыми идеями, касающимися построения машин, которые в значительно большей степени приблизятся к свойствам мозга, чем
449
Человек играет в шахматы с машиной.
ныне существующие машины. Возникло и успешно развивается новое научное направление - бионика. Цель ее - перенести в технику многие интересные свойства живых организмов. Особый интерес представляет поразительная чувствительность некоторых органов чувств у отдельных животных, например органа обоняния у собаки. Интересны также способы, с помощью которых из относительно малонадежных нервных клеток составляется такая надежная в целом управляющая система, как человеческий мозг.
Кибернетика непрерывно совершенствует свою техническую базу. На смену громоздким и малонадежным ламповым машинам пришли машины, использующие полупроводники и магнитные элементы. Успехи современной физики позволят сделать следующий шаг: перейти к чрезвычайно миниатюрным элементам, использующим тонкие пленки, твердые схемы и другие элементы. Это позволит сделать машины чрезвычайно надежными, малогабаритными, относительно дешевыми и простыми в эксплуатации. Происходит также непрерывное совершенствование логической структуры машин, увеличение быстроты их действия и объема памяти. Наряду с этим разрабатываются методы построения новых машин, копирующих
не только функции, но и некоторые детали внутреннего строения человеческого мозга.
На базе новых и новейших кибернетических устройств и систем быстрыми темпами развивается автоматизация различных видов умственной деятельности человека. Автоматизация эта захватывает все новые и новые области, возможности ее безграничны. У ряда буржуазных философов и писателей успехи подобной автоматизации вызывают опасения за будущность человечества: не будет ли человек полностью вытеснен автоматами? Однако подобные опасения возникают лишь в результате непонимания закономерностей исторического развития. В капиталистическом обществе действительно происходят подобные процессы: успехи кибернетики и внедрение вычислительных машин приводят к безработице, к вытеснению человека машиной. Однако виновата в этом не кибернетика, а капитализм. В социалистическом и коммунистическом обществе, которое с исторической неизбежностью приходит на смену капитализму, не может быть и речи о вытеснении человека машиной. Машины, какими бы совершенными они ни были, всегда останутся верными помощниками человека, способствуя неизмеримому расцвету материальных и духовных сил человеческого общества.
450
Электронная вычислительная машина «Урал-2» (фото вверху) в роли диагноста в Институте им. А. В. Вишневского в Москве. Симптомы излагаются на перфорированной кинопленке, которая закладывается в приемную часть машины (фото внизу).
Получив задание, машина молниеносно выдает ответ, называя одну или несколько болезней, имеющих тождественные симптомы.
Пусть a и b - произвольные положительные числа. Тогда:
(a + b) ⁄ 2 - среднее арифметическое чисел a и b,
√‾ab - среднее геометрическое чисел a и b,
2ab ⁄ (a + b) - среднее гармоническое чисел a и b.
Убедитесь сами, что:
а) Среднее гармоническое равно отношению квадрата среднего геометрического к среднему арифметическому.
б) Если написать подряд: а, (a+b) ⁄ 2, b, то образуются три члена арифметической прогрессии.
в) Если написать подряд: a, √‾ab, b, то образуются три члена геометрической прогрессии.
г) Если взять числа, обратные a и b, составить их среднее арифметическое, а потом снова перейти к обратному числу, то получится среднее гармоническое чисел a и b.
д) Среднее арифметическое a и b не меньше среднего геометрического тех же чисел, а последнее не меньше их среднего гармонического:
(a + b) ⁄ 2 ≥ √‾ab ≥ 2ab ⁄ (a + b)
Докажите, что равенство здесь возможно только при а= b.
е) Если написать подряд: а, 2 ab ⁄ (a + b), b и буквам а, b придать значения а =1 ⁄ k, b =1 ⁄ (k+2), где k - любое целое положительное число, то среднее гармоническое чисел а и b, т. е. 2ab ⁄ (a+b), примет значение 1 ⁄ (k+1), равное среднему члену последовательности:
1 ⁄ k,1 ⁄ (k+1), 1 ⁄ (k+2).
Последовательность такого вида называется гармонической.
Следом за тремя членами этой последовательности можно образовать четвертый член: 1 ⁄ (k+3) затем пятый: 1 ⁄ (k+4) и т. д.
Соединяя члены последовательности знаком «+» и полагая k = 1, получим числовой ряд:
1 + 1 ⁄ 2 +...+1 ⁄ n +...,
который называется гармоническим.
Еще Лейбниц доказал, что сумма 1+1 ⁄ 2+1 ⁄ 3 + ... + 1 ⁄ n бесконечно возрастает, когда n неограниченно растет. Это означает, что, гармонический ряд расходится. Но если перед членами ряда чередовать знаки + и −, то получится сходящийся ряд 1 − 1 ⁄ 2 + 1 ⁄ 3 − 1 ⁄ 4 + 1 ⁄ 5 −1 ⁄ 6 + ..., сумма которого равна натуральному логарифму In 2=0,6993...
Пусть АС=а, ВС= b, АВ = а + b - диаметр окружности; ОЕ^ АВ, DC^ AB. Тогда
ОЕ =(a+b)2, CD = √‾ ab.
Для изображения среднего гармонического проведем дополнительно OD и CF ^ OD. Тогда вы легко докажете, что DF=2ab/(a+b), а также, что C'D² = OD · DF. Тем самым дополнительно будет установлено любопытное соотношение между тремя «средними»: среднее геометрическое двух положительных чисел является средним геометрическим между их средним арифметическим и средним гармоническим.
451
Вавилоняне (2-е тысячелетие до н. э.) удовлетворялись значением π ≈ 3.
Египтяне (2-е тысячелетие до н. э.) считали, что π ≈ 3,16.
Архимед (III в. до н. э.) предлагал на выбор: 310 ⁄ 71 < π < 31 ⁄ 7.
С очень хорошей точностью подобрался к числу π китайский астроном Цзу Чун-чжи (V в.):
π ≈ 355/113= 3,1415929...
Лудольф (XVII в.) имел терпение выявить 35 десятичных знаков после запятой у числа π.
С XVII в. π вычисляют с помощью числовых рядов. Так было получено:
в 1699 г. - 72 десятичных знака,
в 1719 г. - 127 десятичных знаков,
в 1841 г. - 208 десятичных знаков,
в 1853 г. - 261 десятичный знак.
На 20 лет (с 1853 по 1873 г.) растянулось у Вильяма Шенкса вычисление 707 десятичных знаков числа π.
В 1947 г. «хвост» числа π вырос до 808 правильных десятичных знаков.
Не прошли мимо числа π и электронные вычислители. С их помощью было найдено:
в июне 1949 г. - 1120 десятичных знаков,
в сентябре 1949 г. - 2037 десятичных знаков (за 70 часов действия машины),
в январе 1955 г. - 3093 десятичных знака (только за 13 минут),
в январе 1958 г. - 10 000 десятичных знаков (за 100 минут).
В июле 1961 г. Д. Шенкс и Дж. Вренч запрограммировали задание электронной машине: вычислить 100 265 десятичных знаков числа π. И электронный вычислитель блестяще справился с задачей за 8 часов 43 минуты (параллельно та же машина «выдала» столько же цифр и для второй «трансцендентной знаменитости» - числа e).
Исследовав первые 16 000 десятичных знаков числа π, ученые не обнаружили «ненормальностей» в распределении мест, занимаемых каждой из 10 цифр. В этом «хвосте» любая цифра (1, 2, 3, 4, 5, 6, 7, 8, 9, 0) занимает примерно 10% мест от общего числа знаков.
Наша повседневная речь широко использует слово «случай» и его производные - «случайность», «случайный» и т. п. Каждый из нас слышал и сам произносил фразы, подобные следующим: «Я случайно натолкнулся на интересную мысль», «Только случай помог мне сегодня», «Что за приятная случайность помогла нам встретиться». Всякий раз при употреблении подобных выражений в них вкладывается один и тот же смысл: случайные события происходят крайне редко, представляют собой нечто совершенно исключительное, идущее вразрез с установившимся порядком вещей. В обыденном представлении случайное противопоставляется закономерности, является чем-то, что нарушает закономерный ход событий, нормальное их развитие.
Но так ли это на самом деле? Не упрощаем ли мы такими представлениями действительность? Не лишаем ли мы себя существенных возможностей в познании явлений природы, а также процессов техники и экономики, когда считаем, что в мире господствует лишь строгая закономерность определенного типа - каждая определенная ситуация влечет за собой определенные следствия?
Мы сейчас на ряде примеров, заимствованных из окружающей жизни, убедимся в том, что множество важнейших явлений существенно зависит от случая и без учета влияния случайного не может быть полноценного их исследования. Мы увидим, что без учета влияния случайных явления человек становится бессильным направлять развитие интересующих его процессов в желательном для него направлении. Мы узнаем далее, что случайные события также подчинены своим особым закономерностям. Изучение этих закономерностей - задача науки о случайном - теории вероятностей.
452
Почти каждый из нас пользуется телефоном-автоматом. Все мы прекрасно знаем, что иногда приходится долго ждать своей очереди, иногда, же удается позвонить без всякого ожидания. Иногда нужный номер занят, и нам
Иногда нельзя позвонить и потому, что телефон находится в ремонте.
не удается дозвониться даже после нескольких проб; иногда же соединение происходит немедленно, при первой же пробе. Все эти колебания, изменения условий использования телефона не представляют собой ничего необычного, хотя и носят случайный характер.
Известно, что при проведении измерений некоторой величины один результат отличается от другого. Невозможно, чтобы при проведении нескольких замеров все они дали абсолютно тождественные результаты. Этот факт хорошо известен экспериментаторам, и уже давно выработаны действенные меры для исключения случайных ошибок измерения.
Семь раз отмерь, один - отрежь, поскольку при измерениях ты допускаешь случайные ошибки.
Каждый школьник, выполнявший измерения, связанные с физическими или химическими опытами, знает, что для получения более надежного результата опыт следует повторять несколько раз и за лучшее приближение к истине нужно взять среднее арифметическое из полученных чисел. Мы снова столкнулись с влиянием случая в таких событиях, которые систематически выполняются многими тысячами людей в лабораториях заводов, исследовательских институтов, в больницах и в торговых организациях.
При страховании жизни, посевов, скота, имущества никто не может предсказать, что случится в течение года с тем или иным застрахованным, с тем или иным гектаром посева или домом. Может случиться, что с застрахованным лицом произойдет несчастье, посев будет выбит градом или выжжен засухой; ничто не гарантирует нас от падежа скота или пожара, в результате которого погибнет все имущество. Страховые организации при определении размеров страховых взносов и страховых премий в случае несчастий с застрахованным как-то должны учитывать влияние случая и в какой-то мере уметь предсказывать долю тех застрахованных, которым придется выплатить страховую премию. На этом всестороннем учете влияния случая как раз и построено все страховое дело.
Оказывается, размеры ступни взрослых людей подчинены строгой математической закономерности.
Когда предприятия обувной промышленности планируют ассортимент обуви для выпуска в предстоящем году, то они не запрашивают у возможных потребителей, какие номера ботинок и в каком количестве им потребуются. Чтобы не получилось затоваривания обуви тех размеров, которые не потребуются, необходимо научиться заранее рассчитывать долю покупателей с тем или иным размером ног. И хотя ни один магазин не знает в лицо своих покупателей и ни одно обувное предприятие не
453
знает всех своих потребителей, выпуск обуви в общем хорошо удовлетворяет запросы населения. Это основано на изучении размеров ног. Оказывается, здесь приходится иметь дело с одним из законов случая, который получил название теоремы Лапласа - Ляпунова.
Советский Союз с каждым годом расширяет свою внешнюю торговлю и в связи с этим ежегодно значительно увеличивает количество грузовых судов. Для лучшего использования флота необходимо знать те закономерности, которым подчиняется прибытие грузовых судов. На первый взгляд кажется, что здесь нет никакой задачи, так как прибытие и отплытие судов заранее планируются и их движение происходит по строгому расписанию. Однако в действительности это далеко не так: в данный порт приходят суда из многих портов мира, по пути они попадают в различные метеорологические условия, которые существенно влияют на скорость движения. Это обстоятельство влияет на сроки прихода в порт назначения. Закупка товаров у иностранных фирм и иностранными фирмами у нас никак не согласована с графиком прихода судов в порт. Поставка товаров в порт с мест производства также подвержена влиянию множества причин, ни одну из которых заранее учесть невозможно. В результате график прихода судов в порт дает лишь очень суммарное представление об истинной картине загрузки порта. Для примера скажем, что в сентябре 1962 г. из судов, которые должны были прийти по графику в Ленинградский порт, не пришли совсем 17. Вместе с тем прибыли 22 судна, которые не были запланированы. Для того чтобы выяснить, насколько хорошо действуют здесь законы случая, приведем небольшую табличку, в которой указан фактический приход судов с так называемыми генеральными грузами в Одессу за конец апреля и май 1962 г. В первой строчке таблицы указано число судов, прибывших за сутки; во второй - число суток, когда прибывало указанное число судов, и, наконец, в третьей приведены числа суток, вычисленные на основании теории вероятностей, в которые должно прибывать в порт указанное число судов.
Из таблицы мы видим, что согласно законам теории вероятностей должно быть 15,5 суток, когда в порт не должно прийти ни одного судна с генеральными грузами. Фактически таких дней было 16. За рассматриваемый период было 3 дня, когда в порт приходили по 3 судна. Расчет показал, что таких дней должно было быть 2,4. Рассмотренный пример показывает, что и в работе флота должно учитывать влияние случая.
. Приведенные примеры достаточно убедительно показывают, что с игрой случая приходится считаться в большинстве видов человеческой деятельности. Однако убедиться в этом- еще не означает, что становится ясной цель изучения случайных явлений. А ведь всегда полезно видеть, к чему следует стремиться, что может дать обществу вновь приобретенное знание. Мы постараемся выяснить этот вопрос на нескольких примерах.
Что может, скажем, дать нам знание закономерностей случайного прихода судов в порт? В первую очередь ясное представление о числе судов, с которыми придется иметь дело. А это уже многое. Действительно, руководитель порта должен так организовать работу, чтобы прибывающие суда не простаивали в ожидании освобождения причала для погрузки или выгрузки. Сколько нужно причалов, если известен
О качестве всей продукции можно судить и по малой ее части.
грузооборот порта? Если мы поступим чисто арифметически, т. е. разделим количество перерабатываемых грузов на число часов в месяце и число тонн, которое в течение часа способны переработать механизмы порта, то такой подсчет будет ошибочным. Ведь при этом мы не учтем того обстоятельства, что моменты подхода судов случайны. Современная теория вероятностей позволяет произвести расчеты так, что
454
Распределение автотранспорта на отдельных участках шоссе неравномерно. Оно подвержено случайным колебаниям.
будут учтены многие случайные факторы: подходы судов, случайные колебания длительности обработки судна и пр. И при этом можно добиться такого положения, чтобы общая сумма затрат на содержание флота и причалов была минимальной. Таким образом, решение важной экономической задачи опирается на познание случайных явлений.
Когда мы ставим какой-нибудь эксперимент или производим наблюдения, то нас в первую очередь интересует вопрос: сколько измерений нужно произвести или сколько раз следует поставить опыт, чтобы можно было быть уверенным в том, что полученный результат окажется достаточно точным? Поскольку наша задача состоит в том, чтобы уменьшить влияние случайных ошибок измерений, то для исключения влияния случая мы должны знать законы случайных явлений.
Важное и часто встречающееся в практической деятельности использование наших знаний закономерностей случайных явлений проходит по такому пути: о составе большого числа предметов судят по сравнительно небольшой пробе (или, как часто говорят, «выборке»). Так, когда хотят составить представление о длине и крепости волокон хлопка, находящегося в кипе, то совершенно случайно выхватывают из этой кипы небольшой пучок (штапель). По результатам изучения длины и крепости волокон, содержащихся в штапеле, судят о качестве волокна во всей кипе. Этот способ дает прекрасные результаты. И исследование, проведенное буквально над долями грамма, дает надежную основу для назначения последующего технологического процесса, которому должен быть подвергнут хлопок этой партии. Точно таким же способом судят о качестве большой партии зерна по небольшой пробе, взятой из этой партии наудачу. В основе этих широко используемых практических методов лежат общие теоремы теории вероятностей, получившие название законов больших чисел.
При современном промышленном производстве зачастую нет возможности проверить качество каждого отдельного изделия, так как либо этих изделий так много, что на их испытание необходимо потратить многие годы, либо
изделия таковы, что при испытании приходят в негодность. Поэтому испытывают лишь небольшую долю продукции и по ней судят о качестве всей партии. Как следует выбирать такие доли продукции? Как много изделий при этом следует испытывать? Насколько точные результаты при этом могут быть получены? Все эти вопросы таковы, что на них может дать определенный ответ лишь наука о случае. И практика в наше время этим ответом очень широко пользуется. Оказывается, что эти методы дают превосходные результаты, позволяющие экономить средства, материалы, труд и время.
Как и все науки, наука о случае начала развиваться тогда, когда в этом появилась потребность, когда задачи практики уже не могли обходиться выводами, сделанными на глаз, а понадобился точный расчет. Первые шаги в создании теории вероятностей - математической науки о случайных явлениях - были сделаны в середине XVII в., в эпоху зарождения новой математики. Почти одновременно были заложены основы аналитической геометрии и появились ростки, давшие вскоре элементы дифференциального и интегрального исчислений - основы всей современной математики. Этот бурный расцвет математики закономерен. Он был вызван крупными сдвигами в общественных отношениях: развитием торговли, промышленного производства, мореплавания.
Первые понятия теории вероятностей формировались под влиянием потребностей страхования и азартных игр. Страхование в ту пору получило широкое распространение из-за непрерывного роста морских сообщений и морской торговли. Азартные игры захватили феодальную верхушку общества. Множество дворян искали в играх способ поправить свои дела. Наряду с большинством бездумных игроков оказались и такие, которые стремились подметить в случайных ситуациях некоторые закономерности. Один из страстных игроков, кавалер де Мере, обратился с рядом возникших у него задач к крупнейшему математику и мыслителю
455
Когда-то азартные игры помогли возникновению математической теории.
того времени Б. Паскалю. Вот одна из них. При четырехкратном бросании игральной кости что происходит чаще: выпадет шестерка хотя бы раз или же шестерка не появится ни разу?
Посмотрим, как решается эта задача. При бросании одной игральной кости может выпасть одна из 6 граней. В 5 случаях из 6 выпадает грань без шестерки. Если же мы бросим игральную кость один за другим 4 раза, то возможных сочетаний выпавших граней будет значительно больше. Действительно, при двукратном бросании кости число различных сочетаний выпадения граней при первом и втором бросаниях уже будет 36=б² (они записаны в таблице 1).
При бросании кости трижды будет уже б³ различных сочетаний, а при четырехкратном бросании может представиться б4 =1296 различных возможностей. При скольких же возможных исходах ни разу не появится шестерка? Из нашей таблички видно, что из 36 возможностей при двукратном бросании кости
в 25 случаях (5²) шестерка не появится ни разу. При четырехкратном бросании игральной кости шестерка ни разу не появится в 54 =625 случаях. Отсюда вытекает, что хотя бы раз при 4 бросаниях шестерка появится в 1296-625=671 случае. Таким образом, при четырехкратном бросании игральной кости хотя бы раз шестерка появляется несколько чаще, чем ни разу. Это открытие, согласно воспоминаниям современников, не без успеха было использовано кавалером де Мере.
Возникновение основных понятий теории вероятностей и правил действия с ними связано с именами математиков XVII в.- Б. Паскаля, П. Ферма, X. Гюйгенса и Я. Бернулли.
Те задачи, которые возникали на заре теории вероятностей, сводились примерно к таким ситуациям: при каждом испытании может появиться одно из n одинаково возможных событий. Интересующее нас событие А появляется тогда, и только тогда, когда происходят определенные т из них. Пример: при бросании четырех костей возможны 1296 различных состояний; из них 625 таковы, что при каждом из них ни разу не выпадает шестерка.
Число случаев, при которых наступает интересующее нас событие А, дает нам средство оценки того, как часто оно может наступить при реальных испытаниях. Однако такой способ оценки неудобен, и в науку было введено следующее понятие: вероятностью события А называется отношение числа случаев, при которых событие А наступает, к числу всех возможных случаев. Вероятность события А мы обозначим символом Р{А}. Таким образом, по определению
Р{А}= m/n.
В нашем примере вероятность того, что при 4 бросаниях ни разу не выпадет шестерка, равна:
Р{ A}= 625/1296
Вероятность же того, что шестерка выпадет
671 хотя бы один раз, равна 671/1296.
Рассмотрим теперь еще одну задачу, относящуюся ко времени возникновения теории вероятностей. (Рассказывают, что с этой задачей обратился к X. Гюйгенсу один из ландскнехтов - наемных солдат.) При одновременном бросании трех игральных костей какая сумма выпавших на них очков должна появляться чаще - 11 или 12? Ландскнехт заметил, что
456
и та и другая сумма может осуществиться шестью различными способами, а именно:
11=1+4+6=1+5+5=2+3+6=2+4+5=3+3+5=3+4+4,
12 =1+5+6=2+5+5=2+4+6=3+3+6=3+4+5=4+4+4.
Словами: сумма 11 может появиться только тогда, когда или на одной из костей появляется 1, на другой 4 и на третьей 6, или и т. д. Точно так же 12 может появиться только тогда, когда или на одной кости появится 1, на другой 5, на третьей 6, или и т. д.
Казалось бы, 11 и 12 должны появляться одинаково часто, предполагал ландскнехт, однако его долголетний опыт учит другому: 11 появляется несколько чаще, чем 12. В чем же здесь причина?
Мы уже знаем, что всех различных исходов при бросании трех игральных костей будет 216. Теперь задача состоит в том, чтобы подсчитать число всех одинаково возможных исходов, при которых в сумме появляется 11 и 12. Мы увидим при этом, что одинаковое число разложений 11 и 12 на сумму трех слагаемых еще не является достаточным основанием для заключения равенства вероятностей этих событий. Все дело в том, что не все эти суммы одинаково часто встречаются. Так, все суммы, 3 которых все три слагаемых различны при подсчете числа возможных исходов, должны быть взяты с большим весом, чем остальные. Действительно, разложение 11 на сумму слагаемых 1+4+6 может произойти шестью различными способами: (1, 4, 6), (1, 6, 4), (4, 1,6), (4, 6, 1), (6, 1, 4), (6, 4, 1). Мы мысленно нумеруем кости и на первом месте указываем число очков, выпавших на первой кости, на втором - на второй кости и на третьем - на третьей.
Точно так же суммы, в которых два слагаемых одинаковы, например 1+5+5, могут осуществиться лишь тремя различными способами: (1, 5, 5), (5, 1, 5), (5, 5, 1). И, наконец, сумма 4 + 4 + 4 осуществляется одним-единственным способом: (4, 4, 4).
Если теперь учтем только что сказанное, то окажется, что число случаев, при которых в сумме появляется 11, равно: 6+6+6+3+3+3=27, а при которых появляется 12, равно: 6+6+6+3+3+1=25. Таким образом, получаем, что:
Р {11} = 27/216, Р {12} = 25/216 .
Мы теперь же должны сказать, что расширение области применений теории вероятностей убедительно показало недостаточность того классического определения вероятности, которым мы пользовались, и установило необходимость широкого его обобщения. Такое обобщение сейчас уже произведено, и пока оно удовлетворяет всем запросам как практиков, так и теоретиков. Тем не менее классическое определение вероятности оказалось исключительно полезным для современного естествознания; оно лежит в основе многих важных заключений.
Прежде всего рассмотрим две важные формулы, которые лежат в основе действий с вероятностями. Эти формулы носят название теорем сложения и умножения вероятностей. Пусть два события А и В таковы, что при каждом испытании может появиться только одно из них или же ни одного, а вместе появиться они не могут. Такие события называются несовместными. Теорема сложения утверждает, что если А и В несовместны, то
Р{А или В}=Р{А} + Р{В}.
Представим теперь себе, что события А и В таковы, что наступление одного из них не изменяет вероятности наступления другого. Такие события называются независимыми. Для независимых событий имеет место теорема умножения, состоящая в следующем:
Р{А и В}=Р{А}·Р{В}.
Рассмотрим для иллюстрации следующую задачу, с которой в настоящее время приходится часто встречаться при организации производства. Ремонтный рабочий обслуживает 6 механизмов, каждый из которых независимо от других может выйти из нормального рабочего режима и потребовать к себе внимания. Вероятность выхода каждого из механизмов за период длительности Т равна р. Чему равна вероятность того, что за период длительности Т из рабочего режима выйдет не более чем 2 механизма?
Вероятность того, что данный механизм за весь период работы не выйдет из нормального рабочего состояния, равна 1 - р. По теореме умножения вероятность того, что все шесть механизмов проработают благополучно, равна (1- р)6 .
457
Вероятность того, что определенный механизм выйдет из нормального состояния работы, а остальные пять будут работать хорошо, равна по теореме умножения р (1- р)5. Механизмом, потребовавшим внимания, может оказаться любой из 6, поэтому вероятность того, что из строя выйдет только один механизм (безразлично какой), равна по теореме сложения
6 p (1- p)5 .
Вычислим еще вероятность того, что какие-то два механизма выйдут из рабочего состояния, а остальные четыре будут работать нормально. С этой целью заметим, что по теореме умножения вероятность выхода из строя двух определенных механизмов и нормальной работы остальных четырех равна р² (1- р)4. Но два механизма из шести можно выбрать C²6 = 15 различными способами. Для каждого из них вероятность уже вычислена. В результате по теореме сложения искомая вероятность равна 15 р² (1- р)4 .
Так как интересующее нас событие (выход из нормального рабочего состояния не более чем двух механизмов) может осуществиться следующими несовместимыми способами: все механизмы будут работать безотказно, откажет лишь один механизм, откажут в точности два механизма, то его вероятность по теореме сложения равна:
(1- р)6 +6 р (1- р)5 +15 р² (1- р)4 .
Если, для примера, вероятность выхода механизма из нормального рабочего состояния равна 0,2, то вероятность того, что за указанный срок:
все механизмы будут работать нормально, равна 0,262144;
только один механизм выйдет из строя, равна 0,393216;
только два механизма выйдут из строя, равна 0,245760.
Таким образом, при указанных условиях работы искомая вероятность равна 0,90112.
Дополнительные исторические сведения
Конец XVIII и XIX век принесли множество новых задач, связанных со случайными явлениями. Прежде всего бурное развитие астрономии, физики, химии, точных технических измерений со всей остротой поста-
вило задачу построения теории ошибок измерений. Почти одновременно основы современной теории ошибок наблюдений были созданы двумя крупнейшими математиками - А. Лежандром и К. Гауссом. Далее, развитие военного дела потребовало развития теории стрельбы. Пока стрельба велась на малые расстояния по видимым целям, задача прицела, например,
При многократной стрельбе по мишени попадания выявляют определенную закономерность.
совсем не могла даже возникнуть. Исключительное значение для прогресса всего естествознания и науки о случайных явлениях имело развитие молекулярных концепций в физике. Создание кинетической теории газов с особой силой потребовало систематического изучения теории случайных величин.
Такие выдающиеся математики, как П. Лаплас, С. Пуассон, П. Л. Чебышев, A. M. Ляпунов, А. А. Марков, обогатили теорию вероятностей рядом замечательных открытий.
Вместе с тем во второй половине XIX в. стала все сильнее ощущаться необходимость создания новой математической дисциплины, которая получила название математической статистики. Среди простейших вопросов, которые относятся к ней, упомянем лишь следующий. Допустим, нам неизвестна вероятность р случайного события А. Как оценить ее значение? С этой целью производят некоторое число n независимых испытаний, в каждом из которых событие А появляется с неизменной вероятностью p, нам неизвестной. Далее подсчитывают число появлений события А. Отношение этого числа к n дает нужную оценку.
458
В наши дни математическая статистика приобрела особенно большое значение. На ее правилах и результатах основаны, в частности, методы анализа производственных процессов, текущий и приемочный статистический контроль качества массовой промышленной продукции, оценка наличия или отсутствия сигнала на фоне шума и пр.
Мы ограничимся здесь формулировкой двух теорем, получивших многочисленные теоретические и практические применения. Первая из них была доказана Я. Бернулли и опубликована в 1713 г.
Производится последовательность независимых испытаний, в каждом из которых событие А может произойти с одной и той же вероятностью р. Пусть среди первых n испытаний событие А наступило в некоторых m . Тогда, как бы мало ни было взято e >0,
Таким образом, если взять n достаточно большим, то вероятность неравенства │ m/n- р │ > e
становится как угодно малой. А так как события с малой вероятностью имеют мало шансов наступить, то мы видим, что при больших n, как
правило, отношение m/n будет близко к р.
Теорема Я. Бернулли служит базой для приближенной оценки неизвестных вероятностей случайных событий. Длительные наблюдения над рождениями установили, что в среднем на каждую 1000 рождений приходится 511 мальчиков и 489 девочек. Отсюда делается вывод, что вероятность рождения мальчика приблизительно равна 0,511. По вероятности рождения мальчика делаются серьезные прогнозы о составе населения.
Все страховое дело построено на определении статистическим путем (посредством теоремы Бернулли) вероятностей различных событий: смерти лица определенной профессии в течение определенного года его жизни, гибели от пожара дома, гибели посевов от града и т. д. На этой базе рассчитываются страховые взносы. Эти расчеты оказываются настолько точными, что страховые общества не разоряются, а приносят систематический доход.
Вторая теорема доказана П. Л. Чебышевым в 1867 г. Доказательство Чебышева исключительно просто и изящно. По своим математическим средствам оно вполне доступно учащимся девятого класса. Мы ограничимся формулировкой лишь частного случая теоремы.
Предположим, что случайная величина x может принимать значения x1, х2, ..., хn соответственно с вероятностями p1, р2, ..., рn (p1 + р2 + .. .+ pn =1). Средним значением (математическим ожиданием) случайной величины x называется сумма М x = р1 x1 + p2 x2 +... + pn xn .
Представим теперь себе, что имеется последовательность независимых случайных величин x1, x2,..., x k, ..., каждая из которых имеет среднее значение, равное а, и все случайные величины ограничены некоторым числом с. При этих условиях для любого e >0 имеет место неравенство:
Таким образом, среднее арифметическое независимых случайных величин при большом числе слагаемых становится почти постоянным. Это обстоятельство исключительно важно, оно находит широкое и разнообразное использование на практике. Пусть, для примера, x k есть результат k- го измерения некоторой величины а, лишенного систематической ошибки (например, постоянной ошибки измерительного прибора). Закон больших чисел утверждает, что для получения приближенного значения измеряемой величины следует взять среднее арифметическое из результатов измерений, и чем измерений больше, тем среднее арифметическое будет ближе к измеряемой величине.
В качестве другого примера рассмотрим давление газа на стенку заключающего его сосуда. Это давление есть результат суммарного воздействия ударов отдельных молекул о стенку. Число этих ударов в единицу времени и их сила - дело случая. Таким образом, давление в каждой части поверхности сосуда подвергается случайным колебаниям. Но так как давление складывается из колоссального числа ударов отдельных частиц, то среднее арифметическое отдельных производимых ими давлений, согласно закону больших чисел, практически достоверно является почти постоянной величиной. Отсюда вытекает, что давление газа в нормальных условиях (для не слишком разреженных газов) лишь ничтожно мало колеблется около некоторой постоянной величины. Но это утверждение мы знаем из физики под назва-
459
нием закона Паскаля. Таким образом, мы закон Паскаля получили не как опытный факт, а как результат теории, как следствие из общей теоремы теории вероятностей, из теоремы Чебышева.
Заметим, что теорема Чебышева содержит в себе теорему Бернулли как простейший частный случай, когда все случайные величины могут принимать лишь два значения 0 и 1, соответственно с вероятностями 1- р и р.
Основными понятиями, обогатившими современную теорию вероятностей, следует считать понятия случайного процесса, случайного поля, информации.
Известно, что физика, химика, биолога и техника интересует в первую очередь изучение процессов, т. е. явлений, протекающих во времени. Так, при изучении химической реакции или же в технологических процессах на химическом предприятии нас всегда интересует, как при заданных условиях эта реакция протекает во времени, какая часть вещества уже вступила в реакцию, когда практически реакция уже закончилась.
Представим себе, что мы задались целью проследить за движением какой-либо молекулы газа или жидкости. В случайные моменты времени эта молекула сталкивается с другими молекулами, меняет при этом свою скорость и направление движения. Ряд физических задач требует для своего решения умения вычислять вероятности того, как много молекул успеет за тот или иной промежуток времени передвинуться на то или иное расстояние. Так, например, если приведены в соприкосновение две жидкости, то начинается взаимное проникновение молекул одной жидкости в другую- происходит диффузия. Как быстро протекает процесс диффузии, по каким законам, когда образующаяся смесь газов становится практически однородной? На все эти вопросы дает ответ статистическая теория диффузии, в основе которой лежат вероятностные расчеты.
Весьма важный круг явлений происходит по принципу радиоактивного распада. Это явление, как известно, состоит в том, что в случайные моменты времени какие-то атомы
радиоактивного вещества распадаются, превращаясь в атомы другого вещества. Каждый распад происходит подобно взрыву, с выделением некоторой энергии. Если масса распадающегося вещества не слишком велика (меньше определенной величины, называемой критической), то распады атомов, как показывают многочисленные наблюдения, происходят независимо друг от друга. Для изучения процесса радиоактивного распада весьма важно определить вероятность того, что за определенный промежуток времени распадается то или иное число атомов. Впрочем, в точности такая задача возникает в телефонном деле, при проектировании пропускной способности мостов, в теории надежности, в экономике, в военном деле, в технике. Независимо от конкретного воплощения, вопрос, который постоянно возникает, ставится так: как велика вероятность того, что за определенный промежуток времени наступит некоторое число определенных событий (вызовов абонентов на телефонную станцию; машин, которым требуется пересечь мост; отказов элементов, из которых составлено сложное оборудование, и т. д.)? При весьма широких условиях искомая вероятность может быть вычислена по формуле:
Здесь Pk (t) означает вероятность того, что за промежуток времени t произойдет ровно k событий; l - постоянная, так называемая интенсивность наступления событий, е =2,71828..., k ! =1·2·3· ... · k.
В начале статьи была приведена небольшая табличка приходов судов в Одесский порт. Нижняя строка таблички вычислялась как раз по этой формуле. Эта же формула широко используется в физике для подсчета числа космических частиц, попадающих на определенный участок земной поверхности за время t. Она же служит для вычисления числа ламп в электронной вычислительной машине, которые перегорят за срок t. Эта формула дает прекрасное совпадение с фактически наблюдаемым числом вызовов на телефонной станции.
Рассмотрение задач естествознания не с точки зрения качественного, а с позиций их количественного изучения привело к формированию понятия случайного процесса. Первые идеи в этом направлении были высказаны биологами и физиками еще в конце прошлого века. Более определенную форму они приняли в работах физиков А. Фоккера и М. Планка. Одна-
460
ко точное определение и начала теории впервые были построены А. Н. Колмогоровым и А. Я. Хинчиным. Первому из них принадлежит заслуга в создании основ так называемых марковских процессов, второму - стационарных процессов.
На базе этой теории строятся далеко идущие заключения в физике, химии, аэродинамике, радиотехнике, биологии, геофизике и экономике.
Теория вероятностей - наука о случайных явлениях - в настоящее время находится на крутом подъеме. К ней теперь обращаются и физики, и астрономы, и экономисты, и лингвисты. Без нее не может быть глубокого познания процессов образования помех при радиовещании, правильного расчета организации производства, создания рациональных способов приема больших партий продукции, расчета запасов и средств обороны.
Прогресс теории вероятностей и ее применений требует непрерывного пополнения творчески работающих в ней математиков способной молодежью. Несомненно, среди читателей Детской энциклопедии будет и та часть молодежи, которая даст новых Лапласов и Чебышевых.
Рыбоводу понадобилось определить, сколько в озере рыб, годных для улова. Следуя рекомендации теории вероятностей, рыбовод забросил сеть с заранее выбранным размером ячеек и, вытащив ее, пересчитал добычу. Рыб оказалось 38. Сделав пометку на каждой рыбке, рыбовод всех их выпустил в озеро.
На другой день он опять забросил ту же самую сеть и теперь выловил уже 53 рыбки, две из которых оказались мечеными. По этим данным рыбовод и вычислил приблизительно количество рыб в озере, годных для улова данной сетью.
К какому результату пришел рыбовод?
Решение на стр.471.
Известно, что истоки каждой науки лежат в запросах практики, в тех задачах, которые выдвигает перед человечеством жизнь. Развитие общества, научные открытия, прогресс техники и экономики непрерывно выдвигают новые задачи, требующие для своего решения новых методов и приемов. В результате каждое поколение должно постоянно продвигаться вперед и никак не может ограничиться теми знаниями и умением, которые достались ему от прошлого.
Одним из наиболее характерных направлений развития современной техники и экономики, а также многих областей науки является не только автоматизация отдельных операций и целых производственных процессов, но и автоматизация самих процессов управления. Аппаратура, которая используется для этой цели, усложняется с каждым годом. Это вызвано в первую очередь тем, что на такие устройства возлагаются все более и более ответственные задачи. И нужно признать, что без такого усложнения не были бы возможны многие поразительные успехи, достигнутые за последние годы. Так, без сложных систем дистанционного управления было бы немыслимо наладить эксплуатацию атомных электростанций или осуществить такие небывалые операции, как фотографирование обратной стороны Луны. А какие колоссальные и сложные вычисления производят быстродействующие электронные вычислительные машины! Но здесь возникает явное противоречие: чем сложнее такие управляющие устройства, тем выше предъявляемое к ним требование надежности, т. е. способности совершенно безотказно выполнять свои функции.
Действительно, нетрудно представить себе, что произойдет, если откажет система управления или серьезно изменится режим ее работы на атомной электростанции или в автоблокировке на железной дороге: могут погибнуть не только материальные ценности, но и люди. Отказ автоматического управления крупной энергосистемы приведет к тому, что парализованной окажется промышленность того или иного района, без электроэнергии останутся водонапорные станции, транспорт, лишатся света боль-
461
ницы и школы. А если ненадежное устройство управляет большим химическим производством? Ведь никакого управления химическими реакциями фактически не будет. В результате получится продукция низкого качества, понизится выход готового продукта из используемого сырья и может создаться взрывоопасная ситуация. Известны случаи, когда на совершенных по инженерному замыслу автоматических линиях из-за плохого управляющего оборудования нарушается технологический режим. В результате изготовляется нестандартная продукция, требующая ручной доделки.
Но не только для автоматизации производственных процессов или запуска космических кораблей нужна высокая надежность аппаратуры. С требованием высокой надежности мы сталкиваемся повсюду. Самолеты должны летать без аварий и послушно выполнять волю пилота, автомобили - безотказно перевозить грузы и пассажиров, станки - обрабатывать изделия с заданной точностью, искусственное сердце или искусственные почки - безупречно выполнять свои функции во время сложнейших операций.
К сожалению, еще далеко не все изделия обладают той надежностью, которая необходима. Иногда покрышки для автомобильных колес выходят из строя слишком скоро и многие автомобили стоят без движения: их не во что «обуть». Из-за поломки тех или иных частей у нас в стране простаивает около 40% грузовых автомобилей. Этим наносится огромный материальный ущерб народному хозяйству -ведь для ремонта автомобилей нужно строить заводы запасных частей, авторемонтные заводы, затрачивать рабочую силу, материалы и средства.
Особенно высоки требования к надежности той аппаратуры, которую трудно или невозможно исправить. А такой аппаратуры теперь в распоряжении человечества уже много и будет все больше, как мы об этом уже говорили.
Чтобы представить себе сложность современной аппаратуры, рассмотрим этот вопрос лишь с чисто арифметической стороны, не вдаваясь в технические детали. Современная электронная вычислительная машина, производящая огромные вычислительные работы, решающая логические задачи - перевод с одного языка на другой,- управляющая процессами автоматизации различных производств,- сложное устройство. В ней многие тысячи диодов и триодов, конденсаторов, сопротивлений,
элементов памяти (ферритовых колечек), подводящих проводов и пр. Каждый из составляющих элементов неабсолютно надежен и имеет положительную вероятность выйти из строя в любой промежуток времени.
Для того чтобы такое сложное оборудование действовало, необходимо каждый элемент поддерживать в рабочем состоянии. Представьте себе, к чему может привести отказ одного-единственного элемента, например обрыв подводящего провода в работе автопилота, установленного на самолете, управляемом по радио!
Вот почему так важно заранее, до выпуска массовой продукции, научиться рассчитывать ее надежность, а также выбирать из различных вариантов какого-нибудь устройства тот, который будет обладать наибольшей надежностью при сохранении прочих необходимых качеств. В этих расчетах обойтись без математических методов невозможно. Вот почему в теории надежности математика занимает значительное место.
На ряде примеров рассмотрим типичные задачи теории надежности и в общих чертах - те математические средства, которые используются при их решении.
Первая задача, с. которой встречаются в теории надежности, состоит в следующем: аппаратура, как правило, выходит из рабочего состояния из-за отказа (т. е. из-за порчи) какого-нибудь составляющего ее элемента. Сколько времени проходит от момента включения элемента до его порчи? В этом вопросе не может быть однозначного ответа. Многочисленные наблюдения и специальные испытания показали, что даже у изделий, изготовленных одновременно в одной партии, время службы далеко не одинаково. Взятый наудачу из продукции, изготовленной одним рабочим за смену, полупроводниковый диод или конденсатор может проработать и несколько десятков тысяч часов и только какую-нибудь сотню часов. Речь может идти не о точном предсказании числа часов, которое проработает элемент, а лишь о вероятности F (t) того, что он проработает не меньше t единиц времени. Хотя для различных категорий элементов функции F (t) имеют различный вид, все же есть и общие черты поведения. Прежде всего в начале работы вероят-
462
ность выхода из рабочего состояния повышена; далее, после окончания этого периода (периода приработки) наступает более или менее длительный период стабильности, когда вероятность отказа за единицу времени остается неизменной; наконец наступает период старения, когда вероятность порчи быстро возрастает.
Важно отметить, что если для отдельных элементов закономерности распределения отказов весьма сложны, то для систем, состоящих из большого числа элементов, удается вывести общие и простые закономерности. Предположим, что каждый испортившийся элемент немедленно заменяется новым. Пусть интересующий нас аппарат состоит из очень большого числа элементов, каждый из которых редко выходит из рабочего состояния по сравнению с отказами хотя бы одного из остальных элементов, и отказы элементов независимы друг от друга. В этих предположениях доказывается следующая важная теорема: вероятность того, что за промежуток времени t произойдет n отказов, приближенно равна:
e ≈ 2,7182..., а l означает положительное число, не зависящее от t. Физический смысл числа l очень прост - это среднее число отказов системы в единицу времени.
Чтобы иметь возможность заранее рассчитать надежность изделия, нужно знать надежность тех элементов, из которых оно будет изготовлено. С этой целью на заводах устраивают испытания и по результатам испытаний делают заключение о качестве элементов. Выбор тех величин, которые должны быть оценены на основании испытаний,- условия, в которых следует производить испытания, а также точность, которую нужно получить в результате испытаний, не могут быть назначены произвольно; они должны определяться физическими и техническими соображениями. В каких условиях придется работать изделию, как долго оно будет находиться в тех или иных условиях? Все это должно быть задано либо конструктором, либо эксплуатационником. Задача математика состоит в выработке плана испытаний: сколько изделий нужно испытывать, в течение какого срока, следует ли отказавшие во время испытаний изделия заменять на новые или нет? Далее, математик должен на основании испытаний выявить наличие связей между теми величинами, которые интересуют практика. Математик же должен указать и тот метод, которым следует пользоваться для обработки результатов наблюдений, а также сделать выводы из этой обработки.
Пусть, для примера, нам известно, что функция F(t), введенная в начале этого раздела, задается формулой: F(t) = e−lt, где l - неотрицательная постоянная. Требуется оценить неизвестную величину X на основании испытаний. С этой задачей приходится часто встречаться в реальной обстановке, поскольку к этой функции неизбежно приводит тот общий результат, который был сформулирован в теореме об отказах сложной аппаратуры.
Среди многих планов испытаний на надежность, предложенных к настоящему времени, мы укажем лишь один: на испытание ставится N одинаковых изделий, отказавшее изделие немедленно заменяется новым, испытания производятся до получения r отказов (например, r =5 или 8). Какие величины необходимо замерять для возможно лучшей оценки неизвестного l ? Математическая статистика учит, что для этой цели достаточно измерить лишь момент наступления r -го отказа. Если он произошел в момент tr, то лучшей оценкой для l будет число
Если же мы отметим дополнительно момент первого, второго и последующих по порядку отказов (t1 < t2 <...< tr), то это дополнительное знание не улучшит оценки величины l .
Понятно, что испытания нужно производить и для того, чтобы наблюдать за ходом производства и за сохранением устойчивости параметров (величин), определяющих качество изделий.
В природе нет абсолютно надежных элементов и изделий. Каждый элемент, как бы совершенен он ни был, со временем теряет свои свойства. Получение элементов сверхвысокой надежности часто либо вообще недоступно существующему уровню техники, либо требует таких больших расходов, что они уже не могут быть оправданы. Приходится для повышения надежности изделий идти другими путями. Один из самых распространенных путей повышения надежности - путь резервирования. Сущность резервирования состоит
463
Резервирование с целью повышения надежности использовали еще воины Чингис-хана.
в том, что в систему вводятся избыточные элементы, узлы и даже целые агрегаты, которые включаются в работу по мере выхода из рабочего состояния основных элементов (узлов, агрегатов).
Так, на железнодорожных станциях стоят резервные тепловозы, готовые в любой момент сменить неисправный рейсовый тепловоз; на крупных аэродромах есть резервные самолеты; на крупных электростанциях - резервные генераторы: они не дают тока в сеть, но в любой момент могут заменить выбывший из строя генератор.
Одна из элементарных задач, которую мы сможем немедленно решить, состоит в следующем. В системе имеются элементы определенного типа; в работе должно постоянно находиться n элементов. Как изменится надежность устройства, если, помимо n основных элементов, в нагруженном резерве (т. е. в таком же состоянии, в каком находятся работающие элементы) находится еще т элементов? Если через р обозначить вероятность того, что данный элемент не выйдет из рабочего состояния в течение необходимого нам времени, то вероятность того, что ни один из n элементов за этот
Случайный отказ может наступить в любой момент, и потому к встрече с ним нужно подготовиться заранее.
срок не выйдет из строя, по теореме умножения вероятностей равна рn. Это вероятность безотказной работы системы элементов, если отсутствуют резервные элементы. Пусть теперь в системе имеется m резервных элементов. В силу теоремы сложения вероятностей вероятность того, что в течение времени t в системе будет сохраняться не менее n исправных элементов, равна1 :
i=0∑m Cm+nn+i · (1 − p) m−i (рис.)
Рассмотрим простой схематический числовой пример. Пусть n =4, m =1, р =0,9. Нетрудно подсчитать, что вероятность безотказной работы системы без резерва равна 0,6561, а при одном резервном элементе становится равной 0,9185. Если бы наша система имела не один, а два резервных элемента, то вероятность ее безотказной работы поднялась бы до 0,9841. Мы видим, что даже небольшое число резервных элементов резко увеличивает надежность системы. Вот почему только один резервный генератор на электростанции почти полностью исключает возможность резкого уменьшения выработки электроэнергии.
Вопросы резервирования становятся более интересными и в математическом и в практическом отношении, когда учитывается дополнительное обстоятельство - восстановление вышедших из строя элементов. В действительности, как только элемент выходит из рабочего состояния, его тотчас начинают ремонтировать (восстанавливать). Так, на вышедшем из строя генераторе либо сменяют пробитую искрой обмотку, либо обновляют другие части.
Среди множества вопросов, связанных с резервированием, отметим сейчас только один: как много элементов необходимо иметь в резерве, чтобы добиться заданной надежности системы? Этот вопрос возникает постоянно в самых разнообразных областях техники. Действительно, для уверенной эксплуатации системы управления нужно знать, какие ее узлы необходимо зарезервировать и какова должна быть кратность резервирования. Подобные же задачи возникают и при расчете резерва генераторов на электростанции, и при оснащении космических кораблей, несущих в космос исследователей и приборы.
1 Это выражение является краткой записью суммы m + 1 слагаемых, каждое из которых представляет собой выражение, стоящее под знаком ∑, где вместо i нужно последовательно подставить числа натурального ряда от 0 до m включительно.
464
Как мы говорили, резервирование требует введения в систему избыточных элементов, а значит, увеличивает ее объем, стоимость и утяжеляет ее. Все эти моменты весьма существенны, особенно для аппаратуры самолетов, космических кораблей, для приборов, которые предназначены для вживления в организм (различные стимуляторы, например стимуляторы сердечной деятельности), для аппаратов, используемых в послеоперационный период, слуховых аппаратов и пр. В такого рода аппаратуре необходимо экономить буквально каждый грамм веса и каждый сантиметр объема. В связи с этим возникает новая интересная задача: найти такое резервирование, при котором система оказывается максимально надежной при ряде дополнительных условий: вес аппаратуры, ее объем и стоимость не должны превышать заданных размеров. Так, для примера, если стоимость блока i-го типа равна Сi, общее число блоков равно m и ni - число блоков i-го типа в резерве, то стоимость резерва равна i=1∑m ni Ci. Если C0 означает ту максимальную сумму, которую можно отпустить на резервирование, то условие, которое накладывается на искомое решение, состоит в следующем:
i=1∑m ni Ci ≤ C0 . (рис.)
Математическая особенность поставленной задачи состоит в том, что мы ищем решение среди целых положительных чисел ni.
При конструировании новых изделий и при расчете возможных улучшений прежних исключительно важно знать, какое влияние на общую надежность системы оказывает тот или иной элемент, тот или иной блок. Это знание позволяет уверенно направлять исследователя на поиски новых, более надежных элементов. Но какие элементы необходимо в первую очередь улучшать? Очевидно, те, которые максимально улучшают надежность системы. Здесь, как это ни кажется парадоксальным, может случиться, что сравнительно ненадежные элементы будут оказывать относительно малое влияние на надежность системы в целом, и нужно улучшать в первую очередь уже весьма надежные элементы. Как это может быть? Очень просто: может случиться, что надежных элементов в системе очень много, а менее надежных - лишь единицы. Для пояснения этого утверждения приведем числовой пример. Пусть в интересующей нас системе имеется шесть элементов первого типа и один элемент второго. Надежность элемента первого типа равна 0,9, а второго - 0,8. Надежность всей системы, в силу теоремы умножения вероятностей, равна 0,96·0,8. Легко подсчитать, что увеличение надежности элемента второго типа на 10% увеличит надежность системы только на 10%. Увеличение же надежности элемента первого типа только на 6% увеличит надежность системы почти на 40%. Этот небольшой подсчет очень поучителен и показывает, как важно инженеру, физику и конструктору уметь пользоваться математическим аппаратом. Такой подсчет может направить мысль исследователя в верном направлении, может показать, где таятся неполадки конструкции.
Мы затронули лишь некоторые вопросы новой науки - теории надежности. Очевидно, многим из наших читателей придется в будущем вплотную заняться задачами теории надежности и развивать ее в разных направлениях - изобретать новые, более надежные элементы, создавать новые надежные схемы, разрабатывать методы исследования и доказывать новые общие теоремы этой теории.
Приготовьте 3 ящика, 3 белых шарика и 3 черных шарика. Положите в первый ящик 2 белых шарика и наклейте этикетку «Б-Б»; во второй ящик положите 2 черных шарика и наклейте этикетку «Ч-Ч»; в третий ящик положите белый и черный шарики и наклейте этикетку «Б-Ч».
Уйдите из комнаты, а ребятам предложите заново разместить шарики по два в каждый ящик так, чтобы все этикетки неправильно указывали содержимое ящиков. Пусть ребята прикроют ящики, чтобы вам, когда вернетесь в комнату, были видны только этикетки, но не шарики.
Теперь, вытащив только один шарик из какого-то одного ящика, вы беретесь точно определить, какие шарики находятся в каждом ящике. Но если хотите удачи, то, разумеется, вам надо сначала обдумать, из какого ящика вы должны вытаскивать шарик и как надо рассуждать, чтобы, зная цвет вытащенного шарика, точно установить, какие шарики находятся в каждом ящике.
Борис взялся за один конец каната, а Аркадий и Николай вместе - за другой. Перетянул Борис, хотя и с большим трудом.
Когда с одной стороны встали Борис и Аркадий, а с другой Владимир с Николаем, то ни та ни другая пара не смогла перетянуть канат на свою сторону. Но стоило только Николаю и Аркадию поменяться местами, как победу одержала пара Владимир и Аркадий.
По нашему убеждению, основанному на точных рассуждениях, самый сильный из этих четырех друзей - Владимир, следующий по силе - Борис, а на последнем, четвертом месте - Николай. Тот из читателей, кто согласен с нашим заключением, тоже должен уметь обосновать его.
465
Что такое теория игр?
Это - математическая теория конфликтов.
А что такое конфликт?
Это - такая ситуация (положение, стечение обстоятельств), в которой сталкиваются интересы сторон, происходит борьба интересов. Каждый из участников хочет чего-то своего, не того, чего хотят другие.
Самые простые примеры конфликтов - это игры (шашки, шахматы, различные спортивные игры). Они отличаются тем, что ведутся по определенным правилам. Правила игры - это система условий, указывающих, какие возможности предоставляются игрокам (перечень возможных ходов); к какому результату (выигрышу, проигрышу) приводит каждая данная совокупность ходов.
Далеко не каждый встречающийся на практике конфликт протекает по правилам. Чтобы сделать возможным математический анализ конфликта, нужно представить конфликт в игровой форме, т. е. указать стратегии (образы действий), возможные для участников, и уточнить, к какому результату приведет игра, если каждый из игроков выберет определенную стратегию. Таким образом, игра есть конфликт с четко сформулированными условиями.
Часто бывает так, что результат конфликта - даже при вполне определенных стратегиях участников - предсказать в точности нельзя, так как он зависит от случая. Такими случайными обстоятельствами, вмешивающимися в ход игры, могут быть, например, тасовка и сдача карт, попадание или непопадание в цель при стрельбе и т. п. Тогда вместо
«результата игры» нужно говорить о среднем результате, т. е. о результате, приходящемся в среднем на одну партию игры, если будет сыграно достаточно большое количество партий. Действительно, в одной партии может случайно «повезти» и игроку, применяющему явно неразумную стратегию. Если же партий будет много, то в среднем выигрывает тот, кто ведет себя разумно.
* Когда мы говорим о результате, или среднем результате, игры, то предполагаем, что этот результат выражается определенным числом. А всегда ли это бывает так? Не всегда. Например, в шахматах мы не всегда выражаем результат числом, а просто говорим: выигрыш, проигрыш, ничья. Но ведь можно условиться и перевести их в числовую форму, например выигрышу приписать значение +1, проигрышу -1, ничьей 0.
Мы будем предполагать, что в любом конфликте выигрыш (проигрыш) каждого из игроков выражается числом. Тогда основную задачу теории игр можно сформулировать так: как должен вести себя (какую, стратегию применять) разумный игрок в конфликте с разумным противником (или противниками), чтобы обеспечить себе в среднем наибольший возможный выигрыш ?
Если в конфликте участвуют две стороны, игра называется парной, если несколько- множественной. Парные игры проще множественных и имеют большее практическое значение. Мы ограничимся только парными играми.
Каждую игру будем рассматривать как конфликт между двумя игроками: К («крас-
466
ные») и С («синие»). Для удобства рассуждений, чтобы иметь какую-то определенную точку зрения, будем обычно становиться на сторону одного из игроков (пусть это будет К) и говорить о нем «мы», а о другом - «противник». Это не означает, что сторона К будет иметь какое-нибудь реальное преимущество. Просто нам так будет удобнее.
Игра называется игрой с нулевой суммой, если одна сторона выигрывает то, что проигрывает другая, т. е. сумма выигрышей К и С равна нулю. В жизни часто встречаются конфликты, в которых это условие не соблюдается. Например, в военном столкновении вполне возможно, что проигрывают обе стороны. Однако во многих случаях можно, не слишком искажая сущность явления, рассматривать парные конфликты как игры с нулевой суммой.
Итак, допустим, что интересы К и С строго противоположны и что сумма выигрышей их равна нулю. Это будет для нас очень удобно в вычислительном смысле. Еще бы! Ведь если выигрыш К равен по величине и противоположен по знаку выигрышу С, то можно рассматривать выигрыш только одного из игроков: выигрыш другого определится автоматически.
Давайте выберем в качестве выигрывающего игрока К. Игрок К заинтересован в том, чтобы обратить свой выигрыш (обозначим его k) в максимум (сделать его наибольшим). Игрок С, наоборот, заинтересован в том, чтобы обратить его в минимум (сделать наименьшим). Каждый из игроков К и C, преследуя свою цель, принимает все меры к тому, чтобы ему было лучше, а сопернику - хуже.
В результате борьбы интересов, если оба противника одинаково разумны, по-видимому, должно быть найдено некоторое равновесное положение, при котором каждый игрок получит то, что ему причитается,- не больше и не меньше. Этот равновесный средний выигрыш, на который вправе рассчитывать игрок К, если обе стороны будут вести себя разумно, т. е. придерживаться своих оптимальных (наилучших) стратегий, называется ценой игры.
Если цена игры равна нулю, значит, это справедливая игра, т. е. она в одинаковой мере выгодна или невыгодна той и другой стороне. Если цена игры положительна, значит, игра выгодна для К. Если отрицательна, придется признать, что она выгодна для С...
Решить игру - это значит найти пару оптимальных стратегий (для К и С) и
цену игры, т. е. средний выигрыш игрока К, если оба - и К и С - будут вести себя разумно.
А если разумно будет вести себя только К, а не С? Ну что же - тем хуже для С! Выигрыш К от этого уменьшиться не может. В худшем случае он останется таким же, а в лучшем - увеличится.
Мы будем рассматривать только конечные игры, т. е. такие, в которых каждый участник располагает конечным числом стратегий.
Если у игрока К имеется в распоряжении т стратегий, а у игрока С имеется n стратегий, игра называется игрой т X п.
Правила игры можно записать в виде таблицы
(или матрицы), в которой m строк и n столбцов. Строки соответствуют стратегиям «красных», которые мы обозначим: K1, К2, ..., Кm, а столбцы - стратегиям «синих»: C1, C2 ... Cn .
В клетках таблицы помещены выигрыши (или средние выигрыши) «красных» при соответствующей паре стратегий. Например, k12 - выигрыш, который получат «красные», если выберут стратегию К1, а «синие» - C2 ; вообще, kij - выигрыш «красных» при комбинации стратегий Кi и Cj .
Такая таблица называется платежной матрицей или просто матрицей игры.
Если конечная игра записана в виде такой матрицы, то говорят, что она приведена к нормальной форме. Но попробуйте, например, записать в нормальной форме обыкновенные шахматы! Вы сразу столкнетесь с тем, что количество возможных стратегий не-
467
обозримо велико - настолько велико, что их перечисление выходит за пределы возможностей не только человека, но и современной вычислительной машины. А жаль! Потому что, если бы построение матрицы шахматной игры было возможно, это имело бы очень любопытные последствия... Но не будем забегать вперед.
Приведем несколько примеров конечных игр. Каждую из них мы запишем в нормальной форме.
Пример 1. Рассматривается игра, которую назовем «Поиск». В ней участвуют две стороны: К и С. К хочет найти С ; С, наоборот, хочет спрятаться от К.
У С есть два места - убежища I и II, где он может прятаться. Выбирает он себе любое убежище. Игрок К по правилам игры тоже может искать С, где ему вздумается. Если он нашел С, С проиграл одно очко, если не нашел, т. е. пошел не в то убежище, где спрятался Г, то, наоборот, К проиграл одно очко. Требуется записать игру в нормальной форме.
Решение. У К - две стратегии:
К1 - искать в убежище I,
К2 - искать в убежище II.
У С - тоже две стратегии:
С1 - прятаться в убежище I,
С2 - прятаться в убежище II. Игра конечная - 2x2, матрица игры будет:
К этой игре мы еще вернемся в дальнейшем и найдем ее решение. А пока что просто порассуждаем за игрока К. Представим себе, что мы игрок К и что нам предлагается выбрать себе стратегию. Что ж, попробуем! Выберем, например, K1, т. е. будем искать всегда в убежище I. Но тогда разумный противник через несколько партий догадается о нашей стратегии и будет прятаться там, где мы его не ищем,
т. е. в убежище II. Плохо! Выберем стратегию К2. Ничуть не лучше: противник снова догадается и будет прятаться в убежище I. Что же нам делать? Попробуем применять стратегии К1 и K2 попеременно, через одну партию игры. Но ведь противник и об этом может догадаться и будет прятаться каждый раз не там, где мы его ищем. Как ни кинь - все клин! Что же, значит, наше положение безвыходно? При любом выборе стратегии нам придется проигрывать? Выходит, что так.
Давайте теперь встанем на точку зрения противника. С удивлением мы обнаружим, что его положение - ничуть не лучше нашего! Какую бы стратегию он ни выбрал - все ему невыгодно.
Позже мы с вами решим эту игру, т. е. найдем пару оптимальных стратегий К и С. Впрочем, о них можно по секрету сообщить заранее: каждому игроку надо будет чередовать свои стратегии, но не регулярно (через одну), а случайным образом (например, подбросить монету и, если она упадет гербом, искать в убежище I, а если цифрой - в убежище II). Аналогично должен будет действовать и С. При этом в среднем на одну партию будет приходиться нулевой выигрыш (цена этой игры будет равна нулю): К не будет ни выигрывать, ни проигрывать. Не очень приятно, но все-таки много лучше, чем всегда быть в проигрыше!
Здесь мы впервые столкнулись с одним из важных понятий теории игр - с понятием смешанной стратегии, т. е. чередования нескольких «чистых» стратегий по случайному закону в определенных пропорциях, или, как говорят, с определенными частотам и. В данном примере каждая из стратегий применяется с частотой 1/2 .
Рассмотрим теперь другую игру, решение которой уже не будет столь очевидным.
Пример 2. Игра «Три пальца».
Два игрока К и С одновременно и не сговариваясь показывают друг другу один, два или три пальца. Если всего показанных пальцев (первым и вторым вместе) будет четное число, то выигрывает К: он получает столько очков, сколько всего было пальцев, если нечетное - выигрывает С, на тех же условиях. Требуется записать игру в нормальной форме.
Решение. Перенумеруем стратегии по числу показанных пальцев. Игра 3x3. Матрица игры будет:
468
Поразмыслим немного над стратегиями каждой стороны. Станем сначала на сторону К. Предположим, что мы выбрали стратегию К1. Что будет делать противник? Он разумен и хочет отдать поменьше. Ясно, он выберет стратегию C2 ; наш выигрыш при этом будет равен -3, т. е. мы потеряем 3 очка. Плоховато! Запишем число -3 против первой строки в добавочном столбце (см. матрицу (3).
Попробуем другую стратегию - К2. На нее разумный противник ответит С3. Мы тогда потеряем 5 очков. Еще хуже! Третья стратегия - К3 - дает точно тот же результат: выигрыш (-5).
Что же делать? Пожалуй, лучше других будет все-таки стратегия К1 - при ней мы по крайней мере не проиграем больше 3 очков! Ведь против этой стратегии стоит максимальное число дополнительного столбца - мы его отметили звездочкой.
Выбрав стратегию К1, мы гарантируем себе, что, как бы ни вел себя противник, мы никак не проиграем больше 3 очков (т. е. не выиграем меньше (-3) очков). Величина (-3) есть максимальный гарантированный выигрыш, который мы («красные») можем себе обеспечить, применяя только одну-единственную стратегию. Такой стратегией должна быть К1 .
Как мы получили (-3)? Нашли минимум каждой строки и из этих минимумов взяли максимальный. Эта величина называется максимином или нижней ценой игры. Будем обозначать ее a .
Подумаем теперь за противника. Он тоже хочет отдать поменьше, а получить побольше. Но, какую бы он стратегию ни выбрал, мы («красные») поведем себя таким образом, чтобы получить с него побольше. Значит, противник («синие») должен в каждом столбце выписать не минимальное, а максимальное число (см. нижнюю добавочную строку в матрице (3).
Из этих максимумов он должен найти минимальный, так называемый минимакс или верхняя цена игры, которую мы обозначим b. Эта величина в нашем случае равна 4 и отмечена звездочкой. Чтобы не проиграть больше 4, «синие» должны придерживаться любой из своих двух стратегий С1 , С2 .
Значит, если каждому участнику предлагается выбрать одну-единственную стратегию, то эти стратегии должны быть: К1 для «красных» и С1 или C2 для «синих».
Как мы выбрали эти стратегии? Руководствуясь принципом осторожности, который говорит: в игре веди себя так, чтобы получить наибольшую выгоду при наихудших для тебя действиях противника. Этот принцип называется принципом минимакса и является в теории игр основным.
Применяя этот принцип, мы пока что рекомендовали игроку К показывать один палец, игроку С - показывать один или два пальца.
Но нашли ли мы решение игры, т. е. такую пару стратегий, которая является равновесным положением? Легко убедиться, что нет. Найденные нами стратегии обладают досадным свойством: они неустойчивы. Действительно, пусть оба игрока держатся рекомендованных чистых стратегий: К1 и, скажем, С1. Пока оба держатся этих стратегий, выигрыш будет равен 2, т. е. на каждую партию игры С проигрывает К два очка. К, может быть, и доволен, но С досадно. Он не хочет проигрывать. Допустим, он откуда-то узнал, что мы придерживаемся стратегии К1. Что он будет делать? Разумеется, немедленно перейдет к стратегии С2 и будет получать по 3 очка, т. е. сведет наш выигрыш к -3. А если мы теперь узнаем о поведении С ? Перейдем на стратегию К2. В ответ на это С переидет на С3 и т. д.
Мы убедились, что пара стратегий, вытекающих из принципа минимакса, неустойчива: стоит одному игроку узнать, что делает другой, как равновесие нарушается...
Всегда ли это будет так? Оказывается, не всегда.
469
Рассмотрим пример. Пусть дана матрица игры (4):
Требуется найти нижнюю цену игры a, верхнюю цену игры b и минимаксные стратегии и проверить, являются ли они устойчивыми.
Решение. Из анализа дополнительных столбца и строки получаем: a = 5, b =5. Максимин равен минимаксу! Случай особый. Что же из этого следует?
Возьмем пару минимаксных стратегий: К2 и С3. Если оба держатся этих стратегий, то выигрыш будет равен 5. Теперь, допустим, мы узнали о поведении противника. Что будем делать? А ничего! Мы по-прежнему будем держаться стратегии К2, потому что любое отступление от нее нам невыгодно. Знаем мы или не знаем о поведении противника - все равно будем держаться стратегии К2 ! То же относится и к «синим» - им нет смысла менять свою стратегию С3 .
В данном примере пара стратегий К2 и С3 устойчива, т. е. представляет собой положение равновесия и дает решение игры.
Почему так получилось? Потому что в матрице имеется особый элемент 5; он является минимальным в своей строке и одновременно максимальным в своем столбце. Такой элемент называется седловой точкой. Если матрица имеет седловую точку (т. е. нижняя цена игры равна верхней), то игра имеет решение в чистых стратегиях: это - пара стратегий, пересекающихся в седловой точке. Сама же седловая точка дает цену игры - в нашем примере она равна 5.
Класс игр, имеющих седловую точку, имеет большое значение в теории игр. В частности,
доказано, что если по правилам игры каждый из игроков знает результат всех предыдущих ходов, как своих, так и противника (так называемая игра с полной информацией), то игра имеет седловую точку и, значит, имеет решение в чистых стратегиях.
Примерами игр с полной информацией могут служить: шахматы, шашки, «крестики и нолики» и т. п.
Приведем пример игры с полной информацией, решение которой легко найти.
Два игрока - К и С - поочередно кладут одинаковые монеты на круглый стол. Положение каждой монеты выбирается произвольно, лишь бы она не перекрывалась другими. Выигрывает тот из игроков, который положит монету последним (когда места для других уже не остается).
Стоит немножко подумать, чтобы убедиться, что исход этой игры всегда предрешен и что существует вполне определенная стратегия, гарантирующая выигрыш тому из игроков, который кладет монету первым (пусть это будет К). А именно К должен положить первую монету в центр стола, а далее на каждый ход С отвечать в точности симметричным относительно центра стола ходом! Бедный С может при этом вести себя как угодно, спасения ему все равно нет...
Очевидно, такая игра имеет смысл только для тех, кто не знает решения. Любопытно, что совершенно так же обстоит дело и с такой популярной игрой, как шахматы! Эта игра имеет смысл только до тех пор, пока не найдено ее решение.
Теоретически доказано, что решение существует и исход шахматной игры в сущности предрешен: если каждая сторона будет пользоваться своей оптимальной стратегией, то игра либо всегда будет кончаться выигрышем белых, либо всегда выигрышем черных, либо всегда ничьей! Но чем же именно? Мы пока этого не знаем, так как число возможных стратегий слишком велико, чтобы можно было построить матрицу шахматной игры и найти в ней седловую точку...
Наверное, любители шахмат заинтересованы в том, чтобы шахматная игра была решена еще не скоро.
Заметим в заключение, что седловых точек в матрице может быть не одна, а несколько; тогда решений игры в чистых стратегиях существует столько, сколько имеется седловых точек. Каждое из них дает выигрыш, равный цене игры.
470
Мы знаем, что если нижняя цена игры a равна верхней b (максимин равен минимаксу), то игра имеет седловую точку и по крайней мере одно решение в чистых стратегиях.
А если a ¹ b ? Можно доказать, что и в этом случае решение всегда есть, только оно лежит не в области чистых, а в области смешанных стратегий. Решением игры называется такая пара стратегий - в общем случае смешанных, систематическое применение которых обеспечивает каждой стороне максимально возможный для нее по условиям игры выигрыш, определяемый ценой игры. Если же одна из сторон отступает от своей оптимальной стратегии (в то время как другая продолжает придерживаться своей), то это ни в коем случае не может быть выгодно для отступающего: это либо оставит его выигрыш неизменным, либо уменьшит. Таким образом, каждая конечная игра имеет решение (возможно, в области смешанных стратегий). Это положение называется основной теоремой теории игр.
Введем специальное обозначение для смешанных стратегий. Пусть К применяет свои стратегии К1, К2, К3 с частотами соответственно р1, р2, р3 (p1 + p2 + p3 =1). Эту смешанную стратегию будем обозначать:
Аналогично смешанную стратегию игрока Г будем обозначать:
Очевидно, любая чистая стратегия - частный случай смешанной, в которой все частоты, кроме одной, равны нулю, а одна - единице.
Решение игры - пару оптимальных стратегий - будем обозначать S * k и S*c, а соответствующий ему выигрыш (цену игры) v.
Очевидно, что цена игры v не может быть меньше нижней и больше верхней цены:
a £ v £ b .
В первом примере мы путем нестрогих соображений догадались, что решение игры должно быть:
а цена игры v = 0. Проверим это. Пусть мы («красные») держимся своей стратегии S*k, т. е. ищем С в убежище I и II одинаково часто, чередуя эти стратегии случайным образом. Может ли С улучшить свое положение (повысить свой выигрыш), отступая любым образом от своей стратегии S*с ? Очевидно, нет. А если одностороннее отступление от стратегии S*k придет в голову нам (в то время как разумный С будет держаться стратегии S*c), то это нам тоже не может быть выгодно. Значит, мы и в самом деле нашли решение игры и ее цену v = 0. Правда, эта игра была довольно простой! Уже второй пример дает игру, решение которой не так очевидно. Из того, что в нем a ¹ b, следует только, что решение нужно искать в смешанных стратегиях.
Но каково это решение? Какова цена игры? Выгодна ли игра «красным», или «синим», или никому из них?
Ответы на эти вопросы вы можете найти в книге, указанной на стр. 509.
Решение к стр.386. Введем обозначения: а - Саша, b - Костя, с - не Саша, d -18 лет, е - 21 год и f - 25 лет.
Мама сказала: «a ·е», папа сказал: «b · d», а дочь сказала: «с· f». Так как часть каждой информации неверна (имеет значение 0), то a · e=b · d=c · f= 0 и а+е=1, b+d=1, c + f =1. Сын Николая Ивановича не может иметь сразу два имени и два возраста; следовательно, а· b = a ·с = d · e = d · e = e · f =0.
Перемножим суммы a + е =1 и b + d =l, тогда a · b+a · d+b · e+e · d= 1; после выбрасывания нулевых членов останется равенство: a · d+b · e =1. Перемножим эту сумму и сумму с+ f =1,что после выбрасывания нулевых членов даст равенство b ·с·е=1, откуда следует, что b =1, с=1 и е=1 (верная информация). Значит, сына Николая Ивановича зовут не Саша (с=1), а Костя (b =1) и возраст его 21 год (е=1).
Решение к стр.461. Пусть число рыб в озере, годных для улова данной сетью, равно х. Тогда отношение числа меченых рыб к числу всех рыб равно 38/ x.
Во второй раз рыбовод выловил 53 рыбы, из них две меченые. Следовательно, отношение числа меченых рыб к числу выловленных равно 2/53.
Будем предполагать, что меченые рыбы равномерно распределились среди всех рыб в водоеме, тогда оба отношения одинаковы: 38 / x = 2 / 53, откуда x=1007.
Значит, в озере имеется примерно тысяча рыб, годных для улова данной сетью.
471
Если бы любому современному математику предложили назвать имена пяти самых крупных ученых его области, то, какие бы он ни выбрал остальные четыре имени, первым будет названо имя Архимеда, великого математика, механика и инженера древности.
Архимед родился в 287 г. до н. э. в Сиракузах - богатом торговом городе Сицилии. Под руководством своего отца, астронома Фидия, получил он первоначальное образование. Очень рано Архимед начал интересоваться астрономией, механикой и математикой. Для завершения образования юноша поехал в Александрию Египетскую - научный и культурный центр того времени. В Александрии жили и работали крупнейшие ученые античного мира - астроном Конон, разносторонний ученый Эратосфен и другие, а несколько раньше там создавал свои знаменитые «Начала» Евклид. Перед Архимедом раскрыла свои богатства и знаменитая Александрийская библиотека, которая насчитывала около 700 тыс. рукописей. Здесь он смог познакомиться с трудами Демокрита, Евдокса и других замечательных греческих геометров.
Наиболее плодотворный период деятельности Архимеда как математика, механика-теоретика и конструктора начался после его воз-
472
вращения в Сиракузы. Уже при жизни Архимеда вокруг его имени создавались легенды, поводом для которых служили его поразительные изобретения, производившие ошеломляющее действие на современников. Известен рассказ о том, как Архимед сумел определить, сделана ли корона царя Гиерона из чистого золота или ювелир подмешал туда значительное количество серебра. Удельный вес золота был известен, но трудность состояла в том, чтобы точно определить объем короны: ведь она имела неправильную форму! Архимед все время размышлял над этой задачей. Как-то он принимал ванну, и тут ему пришла в голову блестящая идея: погружая корону в воду, можно определить ее объем, измерив объем вытесненной ею воды. Согласно легенде, Архимед выскочил голый на улицу с криком «Эврика!», т. е. «Нашел!» И действительно, в этот момент был открыт основной закон гидростатики.
Другая легенда рассказывает, что построенный Гиероном в подарок египетскому царю Птолемею роскошный корабль «Сирокосия» никак не удавалось спустить на воду. Архимед соорудил систему блоков (полиспаст), с помощью которой он смог проделать эту работу одним движением руки. Этот случай или размышления Архимеда над принципом рычага послужили поводом для его крылатых слов: «Дайте мне точку опоры, и я сдвину Землю».
Архимед прославился и другими механическими конструкциями. Изобретенный им бесконечный, или архимедов, винт для вычерпывания воды до сих пор применяется в Египте. Архимед построил планетарий (или «небесную сферу»), который, по-видимому, приводился в движение сжатым воздухом. При движении сферы можно было наблюдать восход Солнца и Луны, фазы и затмения Луны, исчезновение обоих тел за линией горизонта.
Инженерный гений Архимеда с особой силой проявился во время осады Сиракуз римлянами в 212 г. А ведь в это время ему было уже 75 лет! Построенные Архимедом мощные метательные машины забрасывали римские войска тяжелыми камнями. Думая, что они будут в безопасности у самых стен города, римляне кинулись туда, но в это время легкие метательные машины близкого действия забросали их градом ядер. Мощные краны захватывали железными крюками корабли, поднимали их кверху, а затем бросали вниз, так что корабли переворачивались и тонули.
Римляне вынуждены были отказаться от мысли взять город штурмом и перешли к осаде. Знаменитый историк древности Полибий писал: «Такова чудесная сила одного человека, одного дарования, умело направленного на какое-либо дело... римляне могли бы быстро овладеть городом, если бы кто-либо изъял из среды сиракузян одного старца». Только вследствие измены Сиракузы были взяты римлянами осенью 212 г. При этом Архимед был убит. Плутарх сохранил нам яркий рассказ о его смерти: «К Архимеду подошел солдат с мечом в руке, чтобы убить его. Но Архимед настойчиво просил его подождать одну минуту, чтобы задача, которой он занимался, не осталась нерешенной; солдат, которому не было дела до его доказательства, пронзил его своим мечом».
Архимед был замечательным механиком-практиком и теоретиком, но основным делом его жизни была математика. По словам Плутарха, Архимед был просто одержим ею. Он забывал о пище, совершенно не заботился о себе. Главное его внимание было сосредоточено на трех типах проблем:
1. Определение площадей криволинейных фигур или, соответственно, объемов тел. Вы уже знаете, наверное, как определять площади прямолинейных фигур, площадь круга, объем призмы, пирамиды, цилиндра и конуса. Все это умели делать греки и до Архимеда. Но только он нашел общий метод, позволяющий найти любую площадь или объем. Трудно переоценить значение этого метода, без которого была бы немыслима ни физика, ни астрономия. Идеи Архимеда легли в основу интегрального исчисления.
Сам Архимед определил с помощью своего метода площади и объемы почти всех тел, которые рассматривались в античной математике. Лучшим своим достижением он считал определение поверхности и объема шара. Он просил выбить на своей могиле шар, вписанный в цилиндр.
2. Пусть дана некоторая кривая линия. Как определить касательную в любой ее точке ? Или, если переложить эту проблему на язык физики, пусть нам известен путь некоторого тела в каждый момент времени. Как определить скорость его в любой точке ? В школе учат, как проводить касательную к окружности. Древние греки умели, кроме того, находить касательные к эллипсу, гиперболе и параболе. Первый общий метод решения и этой задачи был найден Архимедом. Этот метод
473
Архимед.
впоследствии лег в основу дифференциального исчисления.
3. В математике, физике и астрономии очень важно уметь находить наибольшие и наименьшие значения изменяющихся величин - их экстремумы. Например, как среди цилиндров, вписанных в шар, найти цилиндр, имеющий наибольший объем? Все такие задачи в настоящее время могут быть решены с помощью дифференциального исчисления. Архимед первым увидел связь этих задач с проблемами определения касательных и показал, как с их помощью можно решать задачи на экстремумы.
Огромное значение для развития математики имело вычисленное Архимедом отношение длины окружности к диаметру C / D, т. е.
число p, с большой степенью точности. Для этого он рассматривал последовательность вписанных и описанных правильных многоугольников с числом сторон 6, 12, 24, 48 и 96 и нашел отношения их периметров к диаметру. Ясно, что
pn /D<C/D<Pn /D, где рn - периметр вписанного, а Рn - описанного n -угольника. Архимед нашел, что
310 /71 < p < C/D <3 1/7 .
Продолжая удвоение сторон многоугольников, можно вычислить методом Архимеда сколько угодно знаков числа p .
Идеи Архимеда почти на два тысячелетия опередили свое время. Только в XVII в. ученые смогли продолжить и развить труды великого греческого математика. Только тогда было раскрыто их подлинное значение, таящиеся в них неисчислимые сокровища.
Лейбниц, один из творцов дифференциального и интегрального исчислений, писал: «Внимательно читая сочинения Архимеда, перестаешь удивляться всем новейшим открытиям геометров».
Омар Хайям, один из крупнейших математиков средневекового Востока, родился, вероятно, в 1040 г. и умер в 1123 г. (точные годы неизвестны). Он был уроженцем Нишапура, главного города Хорасана. Хорасан, страна, лежавшая на юго-восток и восток от Каспийского моря, входила тогда в состав государства сельджуков. Теперь значительная часть территории Хорасана находится в Иране, северные районы - в Туркменской ССР, а восточные - в Афганистане.
Более всего Хайям прославился как автор замечательных четверостиший. Воспевая радость человеческого бытия, он вместе с тем порицал несправедливые порядки своего времени и высмеивал официальную религию. Он мечтал о лучшем устройстве жизни на земле:
Когда б я властен был над этим небом злым,
Я б сокрушил его и заменил другим,
Чтоб не было преград стремленьям благородным
И человек мог жить, тоскою не томим.
474
Стихи Хайяма написаны на языке фарси, из которого развились нынешние персидский и таджикский. Сейчас они переведены на русский и многие европейские языки.
В молодые годы Хайяму пришлось много скитаться. Он жил и работал в Самарканде и Бухаре, а в 1074 г. был поставлен во главе обсерватории, организованной в столичном городе Исфахане. Здесь ученый разработал проект нового весьма точного календаря, который не смог, однако, найти применения. Вскоре один за другим умерли покровительствовавшие Хайяму первый министр Низам ал-Мулк и султан Малик-шах, и обсерватория была закрыта. Мусульманское духовенство ненавидело вольнодумца Хайяма. При преемниках Малик-шаха влияние духовенства усилилось и Хайям впал в немилость.
Математические сочинения Хайяма относятся к алгебре, арифметике и геометрии. Они написаны на арабском языке, которым, как правило, пользовались ученые в странах Азии и Африки, покоренных арабами.
Главный труд Хайяма называется «Трактат о доказательствах задач алгебры и ал-мукабалы». Уравнения в то время приводили для решения к нормальному виду, располагая в обеих частях уравнения члены с положительными коэффициентами. Так, например, различали три вида квадратных уравнений x² = рх + q, х² +рх= q и х² + q = рх и для каждого формулировали свой особый прием решения. Уравнение x² + рх + q =0 вовсе не рассматривалось, так как при р³ 0, q³ 0 у него не может быть положительных решений, которые одни принимались во внимание. Операция переноса вычитаемых членов данного уравнения в другую часть, где они оказываются уже прибавляемыми, называлась ал-джабр («восполнение»). Операция приведения подобных членов в обеих частях уравнения называлась ал-мукабала («противопоставление»). От слова ал-джабр произошло наше слово «алгебра», и уже у Хайяма говорится об «алгебраистах».
Трактат Хайяма посвящен в основном кубическим уравнениям. Первые задачи, приводящиеся к кубическим уравнениям с целыми корнями, которые легко найти с помощью простого подбора, появились еще в древнем Вавилоне. Древние греки нашли геометрический прием построения положительных корней кубических уравнений. Прежде всего они применили его к задаче об удвоении куба, т. е. отыскании ребра х такого куба х³, который
был бы вдвое больше данного куба у³. Величину х, т. е. корень уравнения х³ = 2 у³, они построили как абсциссу точки пересечения двух парабол с уравнениями ах= y² и 2 ау = х², отличной от начала координат. Затем Архимед свел к уравнению вида х³ + r = рх² задачу о делении шара плоскостью на два сегмента, объемы которых находятся в данном отношении. Он построил корень этого уравнения как абсциссу точки пересечения некоторых параболы и гиперболы и произвел тщательный анализ задачи.
Проблема Архимеда заинтересовала математиков арабских стран еще в середине IX в. Вскоре здесь занялись и другими вопросами геометрии, приводящимися к уравнениям третьей степени. Такие уравнения получили важное значение и для астрономии, а именно
Омар Хайям.
475
для вычисления необходимых астрономам тригонометрических таблиц. Дело в том, что вычисление синуса 1° можно привести к решению уравнения вида х³ + r = qx. Ученые создали различные приемы приближенного вычисления корней уравнений третьей степени. Наряду с этим возникла потребность в более общей теории.
Наиболее полную для своего времени теорию разработал Хайям, широко применив геометрический метод древних греков. Он рассмотрел все нормальные виды кубических уравнений, которые могут иметь положительные корни. Всего таких видов оказалось 14: одно двучленное, шесть с тремя членами и семь четырехчленных. Для каждого вида Хайям приводит соответствующее ему построение. Так, корень трехчленного уравнения х³ + qx = r выражается абсциссой той точки пересечения
окружности x² + y² =(r/q) х и параболы x² = √‾qy,
которая отлична от начала координат. Анализируя построение, Хайям выясняет, при каких условиях уравнение данного вида имеет один или два положительных корня. Например, уравнение х³ + qx = r при любых значениях коэффициентов имеет один, и только один, положительный корень. Это сразу видно из чертежа. Иногда Хайям указывает границы, в которых лежит корень уравнения того или иного вида. На примерах Хайям показывает, как общая теория применяется к исследованию уравнений с данными числовыми коэффициентами.
Все же в исследовании Хайяма есть пробелы. Так, он не заметил, что уравнение вида x³ + q х = рх² + r может иметь в некоторых случаях три положительных корня. Обнаружить это только с помощью чертежа трудно.
Подобно другим математикам средневекового Востока, Хайям пытался выразить корень кубического уравнения с помощью радикалов, наподобие корней квадратного уравнения. Достичь успеха ему не удалось. Только в начале XVI в. итальянские математики открыли выражение корня кубического уравнения с помощью кубических радикалов. Но уже Хайям пришел к убеждению, что сделать это с помощью квадратных радикалов в общем случае невозможно.
Геометрическая теория кубических уравнений получила дальнейшее развитие как на Востоке, так и в Европе, в частности у Р. Декарта. В XVI - XVII вв. геометрические приемы исследования начинают быстро вытесняться алгебраическими, более совершенными и удобными. Все же до сих пор иногда пользуются геометрическим построением корней уравнений (не только кубических), чтобы примерно определить их значение или получить общее представление о числе положительных и отрицательных корней и т. п.
В алгебраическом трактате Хайям упоминает свой труд по арифметике, в котором он изложил прием извлечения корней любой целой положительной степени из чисел. Ранее были известны способы извлечения квадратного и кубического корней. Этот труд до сих пор не обнаружен. Вероятно, Хайям вывел в нем так называемую формулу бинома Ньютона для целого положительного показателя. Впервые она встречается у другого выдающегося среднеазиатского математика-Насирэддина Туси в учебнике, написанном в 1265 г.
Подобно грекам, математики стран Арабского Востока не имели никаких алгебраических обозначений и все уравнения, преобразования и т. д. записывали словами. Это чрезвычайно удлиняло и затрудняло как исследование, так и изложение. Нашему современнику, приученному к экономной и изящной символической записи, трудно читать старинные трактаты по алгебре.
Хайям написал также комментарии к «Началам» Евклида, в которых разрабатывал теорию отношений и пропорций и учение о параллельных. И здесь Хайям высказал ряд интересных мыслей, оказавших влияние на дальнейшее развитие математики.
Трудно перечислить всех ученых, которые придумали современную «школьную» математику. Но есть два математика, которые сделали для нее больше других: это геометр древней Греции Евклид и «отец современной алгебры» Франсуа Виет.
Франсуа Виет родился во Франции в 1540 г. в городке Фонтеней. Адвокат по профессии, он был всесторонне образованным человеком, хорошо знал древние языки, астрономию. Но его истинным призванием была математика. Увлеченный математической задачей, он мог работать над ней иногда по трое суток без еды и сна. Впет умел активно применять свои способности и знания к всевозможным трудным задачам не только из алгебры или геометрии.
476
Франсуа Виет.
Известно, например, что он любил разгадывать зашифрованные письма. Во время войны Франции с Испанией вся тайная переписка испанцев свободно читалась французами, так как Виет всякий раз разгадывал испанский шифр, как бы его ни запутывали вражеские шифровальщики. Не представляя себе могущества человеческого ума, испанцы думали, что французам помогает дьявол. Они даже жаловались римскому папе и просили его уничтожить эту «дьявольскую» силу.
Виета называют творцом современной алгебры за очень важное открытие - он разработал и последовательно применил в алгебре буквенное исчисление. Чтобы отчетливее представить себе, в чем суть буквенного исчисления Виета и почему оно так важно для всей современной алгебры, посмотрим, что представляла собой алгебра до него. Почти все действия и знаки записывались словами, не было и намека на те удобные, почти автоматические правила, которыми сейчас умеет пользоваться каждый ученик. Нельзя было также записывать и, следовательно, изучать в общем виде алгебраические уравнения или какие-нибудь другие алгебраические выражения. Необходимо было доказать, что существуют такие общие действия над всеми числами, которые от этих самых чисел на зависят. Виет и его последователи установили, что не имеет значения, будет ли рассматриваемое число количеством предметов или длиной перпендикуляра. Главное, что с этими числами можно производить алгебраические действия и в результате снова получить числа того же рода. Не имеет значения также, известно нам число или неизвестно. А если нам не важны цифровая запись или геометрическое истолкование каждого рассматриваемого числа, то все числа как бы однородны и их можно обозначать какими-нибудь отвлеченными знаками, например буквами латинского алфавита. Виет не только ввел свое буквенное исчисление, но сделал принципиально новое открытие, поставив перед собой цель изучать не числа, а действия над ними. Это была удачная мысль, и она стала сразу приносить обильные плоды. Например, вскоре был доказан общий алгебраический закон умножения: умножение отрезков есть та же операция, что и умножение чисел. Появилась возможность записывать алгебраические выражения в виде формул.
Однако у самого Виета алгебраические обозначения, или, как сейчас говорят, алгебраические символы, были мало похожи на наши. Сравните современную запись кубического уравнения
х³ +3 b х= d
и запись этого же уравнения в обозначениях Виета:
A cubus + В planum in A 3 aequatur D solido. Как видите, здесь еще очень много слов, но ясно, что эти слова уже играют роль наших символов, так латинское слово cubus после неизвестного А (неизвестное обозначалось гласной буквой), означает наше «в кубе». Слово aequatur (в переводе на русский - «равный») написано вместо нашего знака «=», умножение чисел В и А обозначено предлогом in (все, что осталось после сокращения от выражения «взять во
477
столько-то раз больше»). Остальные слова - это следы прошлого, следы того, что и у Виета алгебра еще не полностью освободилась от посторонних для нее влияний геометрии.
Такой способ записи и позволил Виету сделать важные открытия при изучении общих свойств алгебраических уравнений. Особенно гордился Виет всем известной теперь теоремой его имени о выражении коэффициентов уравнения через его корни, хотя под корнями он понимал только положительные числа, не признавал за корни отрицательные и совсем не подозревал о существовании комплексных чисел.
При составлении обширных таблиц тригонометрических функций Виет с большим искусством применил десятичные дроби. Глубокий интерес к тригонометрии у него был вызван желанием сделать астрономию более точной. Увлекшись тригонометрией, Виет и здесь получает значительные результаты. Например, он выводит выражения для синусов и косинусов кратных дуг через sin x и cos x при помощи формул, которые мы теперь записали бы в виде:
sin mx =2 cos x sin (m- 1) х- sin (m - 2) х, cos mx = 2 cos x cos (m- 1 )х- cos (m- 2) х.
Эти знания тригонометрии Виет с успехом применял как в алгебре, так и в геометрии.
Используя представление о круге как о пределе вписанных в него многоугольников при увеличении числа их сторон, Виет вычислил число p до 18-го знака после запятой.
Умение решать алгебраические задачи при помощи геометрии и тригонометрии принесло Виету славу победителя турнира лучших математиков того времени. Голландский математик Адриан ван-Роумен предложил математикам всего мира решить уравнение 45-й степени с числовыми коэффициентами. Французским математикам он не послал свой вызов, как бы намекая на то, что во Франции нет математиков, способных справиться с этой задачей. Узнав об этом, король Франции Генрих IV, на службе у которого в то время состоял Виет, восклинул: «И все же у меня есть математик, и весьма выдающийся. Позовите Виета». И действительно, Виет тут же, в присутствии короля, нашел один корень предложенного уравнения, а на следующий день нашел еще 22 его положительных корня. После такого успеха ван-Роумен стал ревностным почитателем Виета.
Виет решил при помощи циркуля и линейки знаменитую задачу, сформулированную геометром древней Греции Аполлонием из Перги. По условию этой задачи надо построить круг, касательный к трем данным кругам. Гордясь найденным решением, Виет называл себя «Аполлонием из Галлии» (Галлией в старину называли Францию).
В последние годы своей жизни Виет занимал важные посты при дворе короля Франции. Умер Виет в Париже в 1603 г. Есть подозрение, что он был убит.
Бурно развивающаяся математика наших дней, конечно, использует идеи и методы, во много раз превосходящие по глубине и общности идеи и методы, которые разработал Виет. Но и сейчас для нас интересна и ценна острая алгебраическая мысль Виета, который широко распахнул перед математикой двери в новый мир современной алгебры. Не будем забывать, что в ее основе лежит буквенное исчисление Франсуа Виета.
Рене Декарт, знаменитый философ и математик, жил и работал в XVII в. В то время передовые ученые и философы Европы боролись с мертвящей властью церкви над наукой. Энгельс писал: «До того времени наука была смиренной служанкой церкви, и ей не позволено было выходить за рамки, установленные верой... Теперь наука восстала против церкви...» Новая наука отвергала всяческие авторитеты и утверждала право человеческого разума и опыта быть единственными проводниками в поисках истины.
Для Декарта самым ясным и точным языком для выражения научных истин был язык математики. Он стремился и в философии, и в науке найти математические законы, свести каждый вопрос или каждую задачу к математической. Декарт хотел создать такой универсальный математический метод, который позволил бы всякому, овладевшему им, решать любую задачу.
Рене Декарт родился в 1596 г. во французском городе Лаэ. Еще ребенком Рене прозвали «маленьким философом» за его любовь к логическим рассуждениям. В школе-интернате из-за слабого здоровья ему разрешали не ходить в класс и заниматься в постели. Рене очень быстро выполнял домашние задания и все свободное время посвящал усиленным занятиям любимой математикой. Необычайная умственная энер-
478
гия сохранилась у Декарта на всю жизнь. После окончания школы юноша три года учился в университете г. Пуатье и получил профессию юриста.
Молодой Декарт с увлечением отдается как науке, так и бурной жизни модного кавалера. Нередко дело доходило до ночной дуэли на улицах Парижа. Это была эпоха мушкетеров, с мужеством которых мы хорошо знакомы по знаменитым романам А. Дюма.
Когда маленькие Нидерланды поднялись на, борьбу за свободу против испанского владычества, Декарт не смог остаться в стороне. Добровольцем-мушкетером вступает он в армию, сражающуюся против испанцев. Но, как говорят историки, ему вряд ли довелось «понюхать пороху» и участвовать в сражениях. Во всяком случае, когда отряд мушкетеров стоял в нидерландском городе Бреды, Декарт больше интересовался вопросами науки, чем войной. Развлекаясь, молодые офицеры писали на городской стене всевозможные трудные задачи и каверзные загадки, предлагая прохожим их решить. Декарт был горячим участником всех этих затей и вскоре познакомился с местными учеными.
Сосредоточенно размышляя над вопросами философии и математики, Декарт настойчиво искал законы универсального метода, стремился дать четкие и общедоступные правила его. Он пишет: «Когда мне приходилось, будучи молодым, слушать о каких-либо искусных умозаключениях изобретательного автора, я пытался воспроизвести их самостоятельно, не читая этого автора. Постепенно я стал замечать, что пользуюсь определенными правилами».
Глубоко изучив психологию творчества, Декарт составил свои знаменитые «Правила для руководства ума». В них он учил, как надо анализировать проблему, разлагая трудные вопросы на более простые до тех пор, пока не появится возможность успешно их решить.
И вот как-то в минуту вдохновения ему представилось, что такой универсальный метод найден - это метод координат, на котором основана аналитическая геометрия.
Обобщая и объединяя известные ему методы координат и буквенной алгебры, Декарт придает своему методу точную и ясную математическую форму. Суть метода Декарта состоит в установлении теснейшей связи между геометрическими объектами и алгебраическими формулами. Эта взаимосвязь устанавливается при помощи системы координат. Если на плоскости задана система координат, то для каждой точки можно определить пару чисел, ее координаты, и, обратно, если дана пара чисел, причем указан порядок их соответствия осям координат, то по ним всегда можно построить на плоскости единственную точку.
Рене Декарт.
Декарт ограничился применением метода координат в плоскости (см. статью «Что такое координаты и для чего они служат?»).
Декартов способ установления связи между точками и числами оказался настолько плодотворным, что, по сути дела, положил начало новой, современной математике. Великий математик и механик П. Лаплас писал, что день, когда Декарт уяснил себе свой метод, можно считать официальным днем рождения современной математики. (История сохранила нам эту дату - 10 ноября 1619 г.)
479
Действительно, при помощи такого аналитического представления точек можно переходить к изучению явлений в многомерных и даже бесконечномерных пространствах, изучать свойства таких интереснейших пространств, как пространства Лобачевского или Эйнштейна. На основе аналитической геометрии выросло и оформилось такое могущественное средство познания природы, как математический анализ.
Декарт много сделал, чтобы придать алгебраической символике максимальную простоту и всеобщность. Предложенные им обозначения сохранились до наших дней. Понимая, что сила математического метода не только в его всеобщности, но и в логической обоснованности, Декарт исследует основное понятие математики - число. Историки считают, что и здесь ему принадлежит слава первооткрывателя современной точки зрения на число. Он вводит в математику, наряду с положительными и рациональными числами, как вполне законные отрицательные и иррациональные числа.
Декарт так описывает применение своего аналитического метода решения задач: «Таким образом, чтобы решить какую-либо задачу, нужно сначала считать ее как бы решенной и обозначить буквами все, как данные, так и неизвестные, величины. Затем, не делая никакого различия между данными и искомыми величинами, заметить зависимость между ними так, чтобы получить два выражения для одной и той же величины; это приводит к уравнению, служащему для решения задачи, ибо можно приравнять одно выражение другому». При помощи системы координат каждому алгебраическому уравнению от переменных х и у можно поставить в соответствие кривую, координаты точек которой удовлетворяют этому уравнению. Таким образом, переходя с языка геометрии на язык алгебры и обратно, можно пользоваться преимуществами обоих способов, обходя многие трудности. Декарт считал, что к алгебраическим уравнениям можно свести все математические задачи. В этом он заблуждался. Дальнейшее развитие математики показало, что важны и интересны многие другие методы и теории. Но и изучение алгебраических кривых, начало которому положил Декарт, представляет собой интересную и быстро развивающуюся область математики.
Много размышлял Декарт над общей теорией алгебраических уравнений. Как и во всем, он искал также и общий метод решения любого алгебраического уравнения. Декарт надеялся, что таким общим приемом может стать разработанный им способ разложения уравнения на произведение множителей более низких степеней методом неопределенных коэффициентов. Он смог дать метод решения уравнения четвертой степени в общем виде.
Однако в XIX в. было доказано, что ни метод неопределенных коэффициентов, ни какой-либо другой не помогут при решении общего алгебраического уравнения пятой или более высоких степеней, потому что такие уравнения вообще не могут быть решены в радикалах. Занимаясь исследованиями алгебраических уравнений, Декарт открыл теорему, которую теперь изучают в школе под именем теоремы Безу. Ему же принадлежит открытие простого способа подсчета числа положительных и отрицательных корней у любого алгебраического уравнения. Это так называемое правило знаков Декарта, с которым можно познакомиться в каждом курсе высшей алгебры.
Последовательно проводя свою мысль о том, что во всем необходимо искать прежде всего физические и математические закономерности, Декарт и животных рассматривал так же, как и явления физики или даже математики. Незрелость самой науки о животных не позволила ему здесь сделать больших открытий. Однако он высказал ряд мыслей, которые лежат в основе большой современной науки - кибернетики.
Понятно, что такое учение, которое в конце концов исключало участие бога в жизни людей и природы, возбуждало ярость церковников и сочувствующих им. По мере распространения учения Декарта его жизнь в Нидерландах становилась все более напряженной. Чтобы избежать доносов и судебных преследований, Декарт воспользовался приглашением шведской королевы Христины. Королева хотела изучать науки под руководством самого Декарта, а заодно пользоваться его советами при создании Шведской академии наук. Декарт переехал в Швецию, но суровый северный климат оказался губительным для его слабого здоровья. Сильно простудившись, Декарт умер 9 февраля 1650 г. Семнадцать лет спустя его останки перевезли на родину, во Францию.
В современной математике доказывается, что универсального метода решения всех задач, о котором мечтал Декарт, нет и не может быть. Но очищенные от посторонних философствований математические идеи Декарта и в наши дни продолжают оставаться плодотворным оружием познаний тайн природы и человеческого мышления.
480
Мы очень мало знаем о жизни этого великого математика. Известно, что он родился в 1601 г. на юге Франции в семье торговца кожами, изучал юридические науки и состоял советником тулузского парламента (суда). Математике он мог посвящать только свободное от работы время. Но сила его гения была столь велика, что, несмотря на это, его идеи наложили глубокий отпечаток на все дальнейшее развитие теории чисел, геометрии и математического анализа. Жизнь Пьера Ферма была скромной, и, по-видимому, он провел ее только в Тулузе и ее окрестностях, не побывав даже в Париже.
Тогда еще не было ни академии наук, ни научных журналов, и отдельные любители науки, разбросанные по всей стране, либо непосредственно писали друг другу, либо посылали письма в Париж к какому-нибудь любителю, который переписывал их и пересылал другим ученым. Так, свои захватывающие мысли и идеи Ферма излагал в письмах к друзьям, среди которых были Р. Декарт, Ж. Роберваль, Б. Паскаль, Ж. Дезарг и другие. И все они считали Ферма величайшим математиком Европы.
Очень немногие сочинения Ферма были изданы им при жизни, и то по настоятельному требованию друзей. Первое собрание сочинений великого ученого появилось только после его смерти. Умер Ферма в 1665 г.
Ферма установил основной принцип геометрической оптики, согласно которому свет распространяется из одной точки в другую по такому пути, для прохождения которого требуется минимальное время. Из этого принципа Ферма выводятся законы отражения и преломления света.
Прекрасный знаток древности, Ферма писал стихи по-гречески и по-латыни. Так же как и Паскаль, он был одним из создателей литературного французского языка. Тот, кто читал его письма в подлиннике, может по достоинству оценить изящество и красоту его стиля. Во время самой острой полемики с учеными, которые иногда, не поняв какого-нибудь из рассуждений Ферма, резко нападали на него, Ферма неизменно сохранял благородное спокойствие, доброжелательство и терпеливо объяснял свою мысль. Из переписки Ферма рисуется именно таким человеком, к которому полностью применимы слова Аристотеля, сказанные по поводу великого математика древности Евдокса Книдского: «Он был образцом умеренности, доброты и силы характера».
Пьер Ферма.
С наибольшей силой гений Ферма проявился в математике. Так, еще до Декарта и в более совершенной форме он построил систему аналитической геометрии, открыл общий метод для определения максимумов, минимумов и касательных, существенно развил метод Архимеда и применил его для определения площадей, объемов и длин дуг. Но любимой его областью, которую он по существу открыл, была теория чисел. Ферма сумел среди множества разнообразных задач и вопросов выделить именно те, которые стали центральными в теории чисел XVIII и XIX вв. Однако он, как правило, не сообщал доказательств своих теорем. Поэтому утверждения Ферма так и остались для последующих ученых проблемами, часть из которых и до сих пор не получила решения.
Остановимся на четырех проблемах Ферма.
1. Занимаясь теорией чисел, Ферма обратил внимание на то, что во всех вопросах арифметики чрезвычайно важную роль играют простые числа: 2, 3, 5, 7, 11, 13, 17, ... Он попытался найти такую формулу, которая при подстановке вместо n целых чисел 1, 2, 3, 4, ... давала бы только простые числа. Ферма полагал, что именно таким будет выражение 2² n +1. Но через 100 лет Л. Эйлер заметил, что хотя при
481
n =0, 1, 2, 3, 4 формула и будет давать простые числа 3, 5, 17, 257, 65 837, однако при n =5 получается число 4 294 967 297, которое делится на 641. Числа вида 2² n +1 носят теперь название чисел Ферма. Они встречаются во многих исследованиях по теории чисел. Однако до сих пор неизвестно, имеется ли среди этих чисел бесконечно много простых или нет.
2. В поисках критерия для определения того, является ли данное число простым, Ферма нашел следующую замечательную теорему: если n - простое число и а - целое число, которое не делится на n, то an -1 - 1 нацело делится на п. Так, например, 56 -1 без остатка делится на 7, а 74 -1 делится на 5. Но 25 -1 не будет делиться на 6, следовательно, число 6 непростое. Эта теорема получила название малой теоремы Ферма. Она была впервые доказана Л. Эйлером, и теперь известно много ее различных доказательств. Она играет фундаментальную роль при исследовании проблем теории чисел и теории групп.
3. Еще большую известность, чем «малая», получила «большая», или «великая», теорема Ферма, в которой утверждается, что уравнение
хn +уn = zn (1)
не имеет целых решений, если только n >2.
Случай n= 2 был рассмотрен еще в древности; тогда же было доказано, что решений у такого уравнения будет бесконечно много. На полях «Арифметики» александрийского математика Диофанта, где излагалась эта задача, Ферма записал свою «великую» теорему. Он добавил, что нашел для нее «поистине чудесное доказательство», однако не может его записать из-за недостатка места. С тех пор прошло около 400 лет, но общее доказательство «великой» теоремы до сих пор не найдено.
Интересна ее судьба. С одной стороны, математики, стараясь доказать теорему, развивали все более и более тонкие методы, открывали новые обширные области для исследований. В настоящее время теорема доказана для всех n £ 10 000.
С другой стороны, эта теорема получила большую известность среди неспециалистов. Их привлекала простота формулировки, а также загадочное замечание Ферма о найденном им «чудесном» доказательстве. Сотни людей тратили и до сих пор тратят свое время и силы, пытаясь доказать «великую» теорему элементарными средствами, ничего не зная об истории этой теоремы и о ее взаимосвязях с современными математическими теориями. Быть может, ни одна из теорем математики не принесла людям так много горьких разочарований и обманутых надежд. Теперь уже ясно, что людям, незнакомым с современной высшей математикой, не следует приниматься за доказательство этой теоремы.
4. «Великая» теорема представляет собой одну из задач так называемого диофантова анализа. Уравнение с двумя или более неизвестными, как, например, хn +уn = zn, называется неопределенным. Одна из главных задач диофантова анализа: узнать, имеет ли заданное неопределенное уравнение с целыми коэффициентами целые решения или нет, а если решения имеются, то конечное ли их число или бесконечное и в последнем случае постараться определить их все (например, так, как это было сделано в древности для уравнения (1) при n =2). Сам Ферма исследовал неопределенное уравнение
x² - а y² = + 1. (2)
В «Началах» Евклида говорится, как найти бесконечное множество решений уравнения х² -2 y² =+1
исходя из наименьшего: x0 =1, y0 =1. Следующее решение будет: x1 =х0 +2у0 = 3 ; у1 =х0 +у0 = 2. И вообще, если xn, yn - решение, то из него можно получить следующее решение по формулам:
xn+1 = x n + 2 yn, yn+1 = хn + y n .
Ферма исследовал уравнение (2) при любом целом неквадратном а. В одном из своих писем он поставил перед математиками следующие задачи: 1) дать способ нахождения наименьшего решения этого уравнения; 2) найти формулы для нахождения всех остальных решений, если наименьшее уже известно. Сам Ферма, безусловно, владел методом решения обеих задач. Чтобы узнать, имеется ли метод у других математиков, он нарочно выбрал такие значения а, для которых наименьшее решение очень велико, и поэтому его трудно найти простым подбором.
Исчерпывающее решение обеих задач было получено только Л. Эйлером и Ж. Лагранжем в XVIII в.
Мы остановились здесь только на нескольких проблемах, которыми занимался великий математик. Но и их достаточно, чтобы оценить силу его гения.
482
Трудно найти другого человека, который оказал бы столь сильное влияние на историю мировой науки и культуры, как Ньютон.
Известный математик и историк науки Б. Л. Ван-дер-Варден пишет в своей книге «Пробуждающаяся наука»: «Каждый естествоиспытатель безусловно согласится, что механика Ньютона есть основа современной физики. Каждый астроном знает, что современная астрономия начинается с Кеплера и Ньютона. И каждый математик знает, что самым значительным и наиболее важным для физики отделом современной математики является анализ, в основе которого лежат дифференциальное и интегральное исчисления Ньютона. Следовательно, труды Ньютона являются основой огромной части точных наук нашего времени». И не только наук: «Математика и техника влияют даже на нашу духовную жизнь, и настолько, что мы редко можем представить это себе полностью. Вслед за необычайным взлетом, которое пережило в XVII веке естествознание, последовал неизбежно рационализм XVIII века, обожествление разума, упадок религии... Кто отдает себе отчет в том,- спрашивает автор,- что с исторической точки зрения Ньютон является самой значительной фигурой XVII века?»
Но, может быть, еще ярче значение Ньютона передает эпиграмма XVIII в.:
Был этот мир глубокой тьмой окутан, Да будет свет! И вот явился Ньютон.
Исаак Ньютон родился в 1643 г. в деревне Вульсторп близ г. Грэнтэма. Отец его был небогатым фермером. Жизнь Ньютона совпала с бурными событиями в истории Англии: революция и гражданская война 1640-1648 гг., казнь короля Карла I, правление Кромвеля, реставрация Стюартов, вторая «бескровная» революция, установление конституционной монархии - вот неполный их перечень, Однако внешне она протекала спокойно и размеренно. Мальчик посещал сначала сельскую школу, а 12 лет его отправили учиться в ближайший город. Директор школы обратил внимание на способного мальчика и уговорил мать Ньютона отправить сына учиться в Кембриджский университет. Ньютон был принят туда в качестве бедного студента, обязанного прислуживать бакалаврам, магистрам и студентам старших курсов.
В университете Ньютон сразу решил посвятить себя физике и математике. Он изучал труды Евклида, Р. Декарта, Дж. Валлиса. Кафедру
Исаак Ньютон.
математики занимал тогда молодой блестящий ученый Исаак Барроу. Он скоро стал не только учителем, но и другом Ньютона, а спустя несколько лет уступил своему великому ученику кафедру математики. К этому времени Ньютон получил уже степени бакалавра и магистра, но материальные затруднения не оставили его. Только получение кафедры дало возможность Ньютону продолжить свои научные исследования.
Трудно представить себе всю интенсивность умственной работы молодого ученого. Наиболее поразительными в его жизни были 1665- 1667 годы. В это время в Англии свирепствовала чума и Ньютон жил в родном Вульсторпе. Именно здесь, в деревенской тиши, молодой Ньютон сделал почти все свои великие открытия
483
в физике и математике. Уже в это время он открыл закон всемирного тяготения и приступил к исследованию с его помощью законов движения планет. Правда, полное подтверждение своему открытию Ньютон получил только в 1672 г., когда было проведено более точное измерение градуса меридиана. В те же 1665- 1667 гг. он открыл дисперсию света и начал конструировать зеркальный телескоп-рефлектор. В нем впервые получилось четкое изображение предмета, без цветного венчика, который давали все прежние телескопы.
Одновременно Ньютон работал над созданием математического аппарата, с помощью которого можно было бы исследовать и выражать законы физики. Такого аппарата еще не было, и каждый ученый придумывал свои методы, обобщая и применяя сделанное еще Архимедом. Ньютон первый построил дифференциальное и интегральное исчисления (он назвал его методом флюксий). Это сразу позволило решать самые разнообразные, математические и физические, задачи. До Ньютона многие функции определялись только геометрически, так что к ним невозможно было применять алгебру и новое исчисление флюксий. Ньютон нашел новый общий метод аналитического представления функций - он ввел в математику и начал систематически применять бесконечные ряды.
Поясним эту идею Ньютона. Известно, что любое действительное число можно представить десятичной дробью - конечной или бесконечной. Так, например:
7/40=0,175; 1/3=0,333 ...; √‾2 =1,412 ...
Это значит, что любое число а можно представить в виде:
где N - целая часть, а a1, а2,..., аn ,... могут принимать одно из значений 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. По аналогии с таким представлением чисел Ньютон предположил, что любая функция от х, например √‾(1 + х), sin x, log (1+ x), может быть представлена как бесконечный многочлен
1 или ряд, расположенный уже не по степеням 1/10,
а по степеням х:
f (х) =а0 + а1 х+а2 х² + ...+ аn хn + ...,
где a1 , а2, ..., аn ,...- коэффициенты, которые каждый раз должны быть определены. Примером такого ряда может служить известная нам геометрическая прогрессия:
1 /( 1 - x) = 1 +х+х² +х³ +... +хn + ...
Представление функции с помощью ряда очень удобно. С помощью рядов, как писал Ньютон, «удается преодолеть трудности, в другом виде представляющиеся почти неодолимыми».
Ньютон нашел основные приемы разложения функций в ряды и показал, как применять ряды в математических исследованиях. Он нашел ряды для представления всех известных в то время функций: √‾(ax+b), тригонометрических и обратных тригонометрических функций, показательной функции, логарифма, функций, заданных с помощью алгебраических уравнений.
Занятия так поглощали Ньютона, что он совершенно забывал об окружающем. Сохранилось немало анекдотов о его баснословной рассеянности. А когда Ньютона однажды спросили, как он мог решать столь трудные проблемы, он ответил: «Постоянным размышлением о них».
Вернувшись в Кембридж, Ньютон изложил письменно свои математические открытия, но не спешил опубликовать их. О части своих исследований он рассказывал в лекциях по оптике, другая часть была известна математикам только по рукописям Ньютона. Первые чисто математические работы Ньютона увидели свет только в 1704 и 1711 гг., самая значительная из них - «Метод флюксий и бесконечных рядов» - была опубликована только после смерти ученого.
В 1672 г. Ньютон был избран членом Лондонского королевского общества, за конструкцию телескопа-рефлектора, а с 1703 г. он становится президентом этого общества и остается им до конца жизни.
Еще в 1680 г. Ньютон, уступая настоятельным требованиям своих друзей-ученых, приступил к работе над книгой «Математические начала натуральной философии», в которой задумал изложить свою систему мира. Работа продолжалась около 5 лет. Об этом периоде жизни Ньютона сохранились записи его секретаря. По его словам, Ньютон был в то время спокойным, приветливым, никогда не впадал в раздражение, почти никуда не выходил из своей комнаты, никогда не садился обедать без
484
многократных напоминаний и чаще всего ел наспех и стоя, спал не более 4 или 5 часов в сутки и каждый час, не посвященный занятиям, считал потерянным. В 1687 г. книга была опубликована. Помимо работы над «Началами», Ньютон много времени посвящал тогда химическим опытам. Он был великолепным экспериментатором.
По единодушному мнению физиков, в истории естествознания не было более крупного события, чем появление Ньютоновых «Начал». В нескольких словах трудно передать все величие этой книги. Положив в основу аксиомы движения, которые теперь известны под названием трех законов Ньютона, и закон всемирного тяготения, Ньютон выводит чисто математически все основные известные в то время факты механики земных и небесных тел: законы движения точки и твердого тела, Кеплеровы законы движения планет (Кеплер установил их на основании наблюдений), закон движения Луны, явления приливов и отливов, форму орбит комет, строит начала гидродинамики. По выражению Д. И. Менделеева, Ньютоном впервые было показано, что возможно с единой точки зрения «охватить весь механизм мировых явлений - от вращения неподвижных звезд до перемещения химических атомов».
Для построения такой системы в то время не было еще достаточного математического аппарата, поэтому в начале своей книги Ньютон строит новую математическую теорию - учение о пределах.
«Начала» произвели сильнейшее впечатление на современников, и еще при жизни Ньютона они издавались 3 раза. Сто лет спустя Ж. Лагранж писал: «Ньютон был величайший гений из всех, когда-либо существовавших, и самый счастливый, ибо только однажды дано человеку открыть систему мира».
Уже будучи президентом Лондонского королевского общества, Ньютон пишет труды, задуманные еще в юности. Среди них - «Оптика», к которой ученый приложил два замечательных сочинения по математике - «О квадратуре кривых» и «Перечисление кривых третьего порядка». Первое из них посвящено вопросам дифференциального и интегрального исчислений, а второе - изучению свойств кривых третьего порядка. Все значение этого последнего сочинения было понято только в XIX в., когда получила развитие алгебраическая геометрия.
Умер Ньютон в 1727 г. в возрасте 84 лет. Он до последних дней своей жизни не прекращал научных исследовании, как теоретических, так и экспериментальных.
Вот что говорил сам Ньютон о своем творчестве: «Не знаю, как на меня посмотрит мир, но самому себе я представляюсь мальчиком, играющим на морском берегу и приходящим в восхищение, когда ему удается порой найти более гладкий, нежели обыкновенно, камушек или красивую раковину; между тем громадный океан сокровенной истины простирается передо мною».
Готфрид Вильгельм Лейбниц родился в Германии в г. Лейпциге в 1646 г. Любознательный мальчик уже 6 лет вел интересные беседы по истории со своим отцом, профессором Лейпцигского университета. К 12 годам он хорошо изучил латинский язык и увлекся древнегреческим. Особенно его интересовали древние философы, и он мог подолгу размышлять о философских теориях Аристотеля или Демокрита. В 15 лет Лейбниц поступает в Лейпцигский университет, где усердно изучает право и философию. Он очень много читает, среди его любимых книг - книги Р. Декарта, Г. Галилея, И. Кеплера и Кампанеллы. Свои колоссальные знания по математике Лейбниц приобрел самоучкой. Через три года, окончив университет, Лейбниц покинул Лейпциг. Он был обижен отказом ученого совета университета присвоить ему степень доктора прав. Отказ объяснили тем, что Лейбниц был... слишком молод!
Началась жизнь, полная напряженного труда и многочисленных путешествий. Легко себе представить, как неудобно было путешествовать в неуклюжих каретах но тряским дорогам Европы тех времен. Лейбниц умел не терять времени даром - много удачных мыслей пришло ему в голову именно во время этих продолжительных поездок. Лейбниц отличался исключительной способностью быстро «входить» в задачу и решать ее наиболее общим способом. Однако гениальных идей приходило в голову Лейбницу больше, чем он успевал их записывать. Чувствуя, что все это богатство мыслей ему не успеть переработать в ясные и завершенные теории, Лейбниц часто ограничивался сообщением только сути идеи. Такая «охота» за идеями была по душе Лейбницу. Он шутливо сравнивал себя с тигром, о котором рассказы-
485
Готфрид Вильгельм Лейбниц.
вают, что если этот зверь не схватит чего-либо в первый, второй или третий прыжок, то предоставляет добыче убежать.
Люди, лично знавшие Лейбница, писали о нем как о мягком и отзывчивом человеке, очень скромном в своих привычках. Лейбниц был дипломатом, надворным советником, воспитателем княжеских детей, историографом. Почти все время он работал при дворах немецких государей, князей и герцогов. Но он всегда помнил о своей любимой науке. Он умел извлекать много полезного из любого дела, любого знакомства. Лейбниц хорошо понимал, что для успешного развития науки необходимы специальные научные общества, академии, в которых ученые могли бы свободно обмениваться мнениями. По предложению Лейбница в 1700 г.
основывается Берлинская академия наук, в которой ему предоставляют почетное место первого президента. Он хлопочет о создании академий в других городах Европы и даже всеевропейской академии наук. Неоднократные беседы Лейбница с Петром I о развитии наук в России имели большое значение для организации Петербургской академии наук. Петр I в знак признания заслуг Лейбница сделал его тайным советником.
Удивительный ум Лейбница породил большое количество плодотворных идей почти во всех областях человеческих знаний. В физике Лейбниц сформулировал основной закон сохранения кинетической энергии, как он ее называл, «живой силы»: mv² /2. Стараниями Лейбница
был положен конец путанице с календарями в Германии и был принят более точный григорианский календарь. Размышляя над философскими и математическими вопросами, Лейбниц убедился, что самым надежным средством искать и находить истину в науке может стать математика. Всю свою сознательную жизнь он стремился выразить законы мышления, человеческую способность думать в виде математического исчисления. Для этого необходимо, учил Лейбниц, уметь обозначать любые понятия или идеи определенными символами, комбинируя их в особые формулы, и сводить правила мышления к правилам в вычислениях по этим символическим формулам. Заменяя обычные слова четко определенными символами, Лейбниц стремился избавить наши рассуждения от всякой неопределенности и возможности ошибиться самому или вводить в заблуждение других. Если, мечтал Лейбниц, между людьми возникнут разногласия, то решаться они будут не в длинных и утомительных спорах, а так, как решаются задачи или доказываются теоремы. Спорщики возьмут в руки перья и, сказав: «Начнем вычислять!» - примутся за расчеты.
Необыкновенная сила этой мысли проявилась прежде всего в творчестве самого Лейбница. При помощи своего универсального исчисления Лейбниц значительно расширил область математики.
Лейбниц, одновременно с Ньютоном и независимо от него, открыл основные принципы дифференциального и интегрального исчислений. Эти исчисления теперь называют математическим анализом. Теория приобрела свою силу после того, как Лейбницем и Ньютоном было доказано, что дифференцирование и интегрирова-
486
ние - взаимно обратные операции. Об этом свойстве хорошо знал и Ньютон. Но только Лейбниц увидел здесь ту замечательную возможность, которую открывает применение символического метода.
Любой человек, изучив небольшое число правил действия с символами, обозначающими операции дифференцирования и интегрирования, становится обладателем мощного математического метода. В наше время такие символы операций называют операторами. Операторы дифференцирования d() и интегрирования ∫() dx действуют на функции, «перерабатывая» их в другие, точно вычисляемые функции (см. статью «Интеграл и производная»). Лейбниц разрабатывает особую алгебру действий с этими операторами. Он доказывает, что обычное число a можно выносить за знак оператора:
d(a f(x))= a d(f(x)).
Одинаковые операторы можно выносить за скобку:
Сокращенно все перечисленные свойства можно выразить соотношением:
d (a f (х) + b j (х))= a d(f(x)) + b d (j (x)),
где a и b - числа.
Операторы, которые обладают таким свойством, называются линейными. Теория линейных операторов, которую с таким успехом начал развивать Лейбниц, в современной математике является хорошо разработанной и полезной в приложениях теорией.
Многократное применение операторов можно понимать как степень оператора; например, для d():
То, что основные операторы математического анализа являются взаимно обратными, Лейбниц подчеркивает своей символикой, утверждая, что d(x) и ∫ () dx так же взаимно обратны, как степени и корни в обыкновенном исчислении. Употребляют так же обозначение, аналогичное обозначению а -1 числа, обратного а, причем произведение а·а -1 = 1. Обозначая операторы: d -1 ()=∫() dx или, наоборот:
и понимая под их произведением последовательное их применение, имеем:
т. е. произведение есть «единица», не меняющая функцию.
Анализируя правила логики, правила рассуждений, Лейбниц увидел, что и здесь можно применить подходящую символику и свести разнообразные приемы умозаключений к небольшому числу точно определенных операций. Такое исчисление умозаключений, или, как его теперь называют, алгебра логики, в наши дни приобрело большое значение. На его основе создаются современные электронные вычислительные машины; теория таких «думающих» автоматов имеет большое принципиальное значение. Всю Вселенную Лейбниц рассматривал как гигантский кибернетический автомат. Отмечая роль, которую сыграли идеи Лейбница для кибернетики, творец кибернетики Н. Винер в шутку писал: «Если бы мне пришлось выбирать в анналах истории наук святого - покровителя кибернетики, то я выбрал бы Лейбница».
Сам Лейбниц также стремился воплотить в машине свои мысли о механизации и автоматизации мыслительных процессов. Он построил металлическую счетную машину, которая могла складывать, вычитать и умножать целые числа. Эта счетная машина произвела большое впечатление на ученых того времени. После того как Лейбниц показал свою машину в Английской академии наук, так называемом Лондонском королевском обществе, его избрали заграничным членом этого общества.
Поиски операторов и исчислений в области систем алгебраических уравнений первой степени со многими неизвестными привели Лейбница к созданию нового важного понятия - определителя системы таких уравнений. О том, что такое определитель, можно подробно узнать в любом курсе высшей алгебры. В наши дни определитель стал совершенно необходимым инструментом как в самой математике, так и в разнообразнейших ее применениях.
Необыкновенная проницательность Лейбница сказывается и в его отношении к математическим играм. Он писал: «Мы часто замечали, что люди проявляют более всего изобретательности в играх, и поэтому математические игры заслуживают внимания... потому что развивают находчивость». В другом месте Лейбниц пишет: «...игры, как требующие ловкости, так и основанные на случайности, дают громад-
487
ный материал для научных занятий». Слова ученого оказались пророческими - современная математическая теория игр имеет огромное значение не только для математики, но и для экономики, военного дела и многих других областей человеческой деятельности.
Смысл всей своей жизни Лейбниц видел в умственном творчестве, в создании общедоступных идей, полезных человеку в познании природы. Надо сказать, что он был честолюбив и очень чувствителен к признанию своих действительных заслуг перед наукой. Тем больнее был для него печально знаменитый спор с И. Ньютоном о приоритете создания математического анализа. И совсем тяжелыми были последние годы жизни, когда старый и больной Лейбниц умирал, забытый всеми. Только необычайная воля к труду и, как всегда, ясная мысль скрашивали его одиночество. Он умер в ноябре 1716 г. Его смерть не была отмечена ни в Берлинской, ни в Английской академии. Его биограф пишет, что он был похоронен как нищий, а не как выдающийся гений Германии. Только спустя много лет в его родном городе была поставлена статуя Лейбница. Но истинным памятником Лейбницу являются его математические идеи, которые и в наши дни продолжают приносить чудесные плоды на благо человека.
Этот крупнейший математик XVIII столетия родился в швейцарском городе Базеле в 1707 г. Отец его был пастором и хотел, чтобы сын тоже стал священником. В Базельском университете Леонард Эйлер штудировал богословие и древние языки, но слушал также лекции по математике профессора Иоганна Бернулли, знаменитого ученого, принадлежавшего к научной школе Лейбница.
Заметив блестящие способности своего слушателя, Бернулли стал с ним заниматься дополнительно. Вскоре математика одержала верх над богословием, и жизненное призвание Леонарда определилось окончательно.
В доме своего наставника Леонард Эйлер завязал дружбу с его сыновьями Даниилом и Николаем, также даровитыми математиками. В маленькой Швейцарии подходящей должности для трех друзей не нашлось. К счастью, в то время в столице России - Петербурге готовилось учреждение Академии наук, и всем троим удалось получить приглашение на работу в ней. Петербургская академия (ныне Академия наук СССР) была открыта в 1725 г., и в том же году приехали в Россию братья Бернулли. Эйлер прибыл в Петербург несколько позднее, весной 1727 г.
Ему было всего 20 лет, но математические дарования чаще всего ярко проявляются уже в молодости. В Петербурге Эйлер попал в круг выдающихся ученых - математиков, физиков и астрономов, получил широкие возможности для издания трудов, полное материальное обеспечение. Он с увлечением принялся за работу, и в ученых записках академии появляются его статьи, привлекающие интерес ученых всей Европы. А вскоре он становится, по единодушному признанию современников, первым математиком мира.
Деятельность Эйлера в Петербурге не ограничилась теоретическими исследованиями в математике и механике. В течение нескольких лет он работает в географическом отделе академии над усовершенствованием карт России. Он пишет большой, двухтомный труд по теории кораблестроения и кораблевождения и одновременно публикует книгу по теории музыки. Ученый ведет занятия со студентами университета при академии и пишет учебник арифметики для школьников. Он неоднократно участвует в различных комиссиях по техническим вопросам. Отдавая всю свою кипучую энергию академии, Эйлер открыто признавал, что всем, чем стал, он обязан прежде всего пребыванию в ней.
Неустойчивое и тревожное положение, создавшееся во время регентства Анны Леопольдовны, заставило Эйлера в 1741 г. перейти на работу в Берлинскую академию наук. При этом он сохранил самые тесные связи с Россией. Эйлер регулярно печатает в изданиях Петербургской академии примерно половину своих статей, редактирует математический отдел ее ученых записок, сообщает в своих частых письмах научные новости и т. д. Годами в берлинском доме Эйлера жили молодые русские ученые, с которыми он вел занятия. Положение дел в Берлинской академии наук во многом не удовлетворяло Эйлера, и в 1766 г. он вернулся в Петербург.
Последние 17 лет жизни Эйлера были омрачены почти полной потерей зрения. Опираясь на свои изумительные способности, он продолжал творить так же интенсивно, как в молодые годы. Только теперь он уже не писал сам, а диктовал ученикам, которые проводили за него и более громоздкие вычисления. О работоспособности Эйлера на склоне лет говорит та-
488
кой феноменальный факт: за 1777 г. он с секретарем подготовил около 100 статей, т. е. почти по 2 статьи в неделю! Когда Эйлер бодрствовал, он размышлял, иногда отвлекаясь для беседы с друзьями и отдыха в кругу семьи. А когда он мыслил, он творил. Этот неустанный творческий труд окончился лишь с жизнью Эйлера - 18 сентября 1783 г.
Научное творчество Эйлера поражает своей плодовитостью. Он оставил более 800 трудов, причем многие из них - большие книги в 2-3 томах. При жизни Эйлера статьи его не успевали печатать. Шутя он говорил, что оставит для академического журнала работ на 20 лет. Великий математик был превосходным вычислителем, но в этот раз он просчитался: посмертные сочинения его печатали еще около 80 лет!
Эйлер был самым плодовитым математиком всех времен. Он был также и самым разносторонним, так как занимался всеми вопросами современной ему математики и ее приложений, а некоторые отделы начал разрабатывать впервые. Теория чисел и теория движения Луны, геометрия и оптические приборы, алгебра и сопротивление материалов, тригонометрия и баллистика - все это и многое другое интересовало его.
Человечество обязано Эйлеру многими ценными изобретениями, усовершенствованиями и техническими теориями. Он заложил основы современной техники изготовления ахроматических зрительных приборов, которые дают изображения, свободные от искажающего рассеяния цветов, благодаря подбору линз с различными показателями преломления. Он создал первую теорию расчета действия турбин. Заложил основы теории гироскопа-волчка, которая играет очень большую роль в современной технике. Но, как ни важны эти заслуги Эйлера, главным в его жизни была разработка проблем математики. Ей он посвятил около 315 сочинений и обогатил эту науку множеством новых теорем, формул, методов, частных теорий и несколькими новыми большими отделами.
Около 150 работ посвятил Эйлер теории чисел. Значение их точно выразил великий русский математик П. Л. Чебышев, продолживший многие исследования Эйлера: «Эти изыскания требовали новых приемов, открытия новых начал, одним словом, основания новой науки. Это было сделано Эйлером».
В геометрии Эйлер положил начало совершенно новой области исследований, выросшей впоследствии в большую и важную науку-
Леонард Эйлер.
топологию, которая изучает общие свойства пространства и фигур. Приведем два замечательных открытия Эйлера, относящихся к топологии.
Первое из них - решение задачи о мостах. Река образует острова, и через два речных рукава перекинуто 7 мостов. Спрашивается, можно ли пройти все 7 мостов так, чтобы каждый был пройден по одному лишь разу. Эйлер показал, что это невозможно, и рассмотрел более общую задачу, в которой речь идет о любом числе местностей, как-либо разделенных рукавами рек и соединенных мостами. Задачу о мостах часто формулируют несколько по-иному, спрашивая, можно ли описать некоторую данную фигуру, составленную из прямых отрезков или дуг кривых, так, чтобы каждое звено было пройдено один, и только один, раз.
Другое открытие представляет важную теорему учения о многогранниках: Эйлер устано-
489
вил и доказал, что числа вершин В, ребер Р и граней Г всякого многогранника, в котором нет дыр, связаны формулой: B +Г=Р +2. Главной областью математических работ Эйлера был математический анализ, т. е. дифференциальное и интегральное исчисления и целый ряд других примыкающих к ним наук. Здесь невозможно даже вкратце перечислить открытия Эйлера в этой области. Упомянем только, что он открыл удивительную зависимость между тригонометрическими функциями (синусом и косинусом) и показательной функцией ех :
exi = cos x +isin x, где i = √‾- 1.
Вместе с тем Эйлер впервые разработал общее учение о логарифмической функции, согласно которому все комплексные числа, кроме нуля, имеют логарифмы, причем каждому числу соответствует бесчисленное множество значений логарифма.
Знаменитый французский ученый П. Лаплас говорил: «Читайте, читайте Эйлера, он наш общий учитель». Действительно, по математическим руководствам Эйлера: «Введение в анализ», «Дифференциальное исчисление», «Интегральное исчисление», «Универсальная арифметика» (т. е. алгебра), по его книгам по механике и физике училось несколько поколений. Главное содержание этих книг вошло и в современные учебники.
Все сочинения Эйлера написаны очень доступно и увлекательно. Юный любитель математики может с пользой и интересом прочитать, конечно с карандашом в руке, первую часть «Введения в анализ». Она читается не так быстро, как приключенческий роман, но с таким же увлечением.
Карл Фридрих Гаусс родился в 1777 г. в небольшом немецком городе Брауншвейге. Отец его был водопроводчиком и в своем городе был известен как хороший вычислитель, так что его часто приглашали для ведения расчетов.
Маленький Карл Фридрих очень рано обнаружил поразительные способности к счету. Впоследствии Гаусс говорил друзьям, что он научился раньше считать, чем говорить. Рассказывают, что, когда ребенку было 3 года, произошел следующий удивительный случай: как-то в присутствии сына отец производил расчет, сколько следует заплатить за работу каменщикам, учитывая, что некоторые из них работали и в обеденные часы. Окончив счет, он собирался уже приступить к выплате денег, как вдруг маленький Карл сказал, что расчет неверен и должно быть столько-то. Оказывается, мальчик в уме повторял все выкладки отца. Велико было удивление последнего, когда, проверив снова счет, он убедился, что сын прав!
Семи лет Гаусс поступил в народную школу. Первые два года, пока учили чтению и письму, мальчик не выделялся среди других. Но на третьем году началась арифметика,- тут-то и проявились его замечательные способности. Учитель как-то задал мальчикам сосчитать сумму чисел: 1+2+3+ ...+40. В то время как другие ученики принялись подряд складывать числа, Гаусс почти сразу подал учителю свою грифельную доску с правильным ответом. Он заметил, что числа, стоящие на одинаковом расстоянии от начала и конца, дают при сложении одинаковое число:
1+40 = 2+39=3+38= ... =20+21=41.
Но всего таких пар чисел будет 20, следовательно, искомая сумма равна: 41·20 = 820.
В это время на мальчика обратил внимание молодой помощник учителя Бартельс. Он начал вместе с Гауссом читать книги по математике. Он же сумел заинтересовать герцога Брауншвейского, рассказав ему о математической одаренности мальчика, и добился, чтобы Гауссу была оказана материальная помощь и он смог продолжать учение.
В гимназии Гаусс очень быстро овладел древними языками и изучил несколько европейских. Окончив ее, юноша поступил в 1795 г. в Гёттингенский университет. Первое время он посещал лекции и по математике, и по филологии, не зная, что ему избрать. В это время у Гаусса были уже собственные математические результаты и он самостоятельно изучал великие творения И. Ньютона, Ж. Лагранжа и Л. Эйлера. Однако посвятить себя математике Гаусс решил только после своего знаменитого открытия о возможности построения правильного 17-угольника с помощью циркуля и линейки. Открытие 19-летнего Гаусса произвело сенсацию: после Евклида, указавшего способы построения правильных многоугольников с числом сторон 3, 4, 5, 3·2k, 5·2k, 4·2k, 15, ни одному математику не удавалось продолжить этот ряд, хотя эта проблема занимала очень многих. Гаусс дал полное решение проблемы, доказав, что если n - простое число вида 22k+1, то соответствующий
490
n-угольник может быть построен циркулем и линейкой. В частности, полагая k =0, 1, 2, 3, получим, что правильные 3-, 5-, 17- и 257- угольники можно построить циркулем и линейкой (а 7-угольник - нельзя). Эта работа была опубликована в 1801 г.
Как ни замечателен сам факт, открытый Гауссом, еще большее значение имел метод, который он применил. Гаусс связал проблему построения правильных многоугольников с вопросом: когда корень уравнения xn−1 = 0 выражается с помощью одних только квадратных радикалов? Гаусс доказал, что это уравнение всегда решается в радикалах, а при n простом и имеющем вид 2² k +1 корень его выражается с помощью одних только квадратных радикалов. Он развил при этом методы, которые позднее легли в основу теории Галуа.
С этого момента начинается героический период творчества Гаусса. На следующие 5 лет падает большая часть его величайших открытий в теории чисел, алгебре и анализе. Вспоминая об этом времени, Гаусс говорил, что новые идеи в таком обилии появлялись у него в голове, что он едва справлялся с ними в сознании, а коротко записывать успевал только часть из них. Это же видно и из дневника Гаусса, в котором он отмечал свои открытия. Так, построение правильного 17-угольника там датировано 30 марта 1796 г., а 8 апреля того же года - первое доказательство квадратичного закона взаимности, одного из основных законов теории чисел. Этот закон был открыт Л. Эйлером, но сам Эйлер не смог доказать его. Гаусс дал этому закону 8 различных доказательств!
В 1797 г. Гаусс предложил новое доказательство основной теоремы алгебры, утверждающей, что всякое алгебраическое уравнение имеет корень (действительный или комплексный), опубликовав эту работу в 1799 г. За нее Гауссу была присуждена степень доктора.
Все свои работы по теории чисел Гаусс собрал в замечательном сочинении, которое положило начало новой эпохе в истории математики, - «Арифметические исследования» (1801).
Эта книга сразу поставила молодого Гаусса в ряд таких математиков, как П. Ферма и Л. Эйлер. В ней впервые строилась теория сравнений и доказывались важные теоремы теории групп.
Но Гаусс был не только великим математиком, пролагавшим своими исследованиями новые пути развития этой науки; он был и замечательным естествоиспытателем. Так, в 1832- 1833 гг. он построил в Гёттингене электромагнитный телеграф.
Карл Фридрих Гаусс.
Он основал также первую в мире магнитную обсерваторию.
Очень рано внимание Гаусса привлекли проблемы астрономии. Ему удалось определить орбиту малой планеты Цереры. Решение этой чрезвычайно сложной математической задачи принесло 24-летнему Гауссу широкую известность. В 1807 г. он был приглашен на пост директора Гёттингенской обсерватории, который не покидал до конца жизни. Одновременно он начал преподавать астрономию в Гёттингенском университете. Результаты своих исследований по астрономии Гаусс объединил в фундаментальном труде «Теория движения небесных тел».
С 1820 г. Гаусс непосредственно руководил геодезическими съемками Ганноверского королевства. Исходя из чисто практических задач, он, во-первых, разработал саму геодезию как науку, а во-вторых, создал свою знаменитую теорию поверхностей. До Гаусса были изучены геометрии только на двух поверхностях: на плоскости (планиметрия Евклида) и на сфере (сферическая геометрия). Гаусс нашел способ построения геометрии на любой поверхности,
491
определив, какие линии играют на поверхности роль прямых, как мерить расстояния между точками на поверхности и т. д. Теория Гаусса получила название внутренней геометрии.
Идеи Гаусса оказали определяющее влияние не только на развитие геометрии, но и на формирование современной физики. Творец теории относительности А. Эйнштейн писал, что его учение очень похоже на теорию поверхностей Гаусса. И действительно, риманова геометрия, созданная по образцу гауссовой теории поверхностей, но только для пространств любого числа измерений, легла в основу теории относительности, так же как евклидова геометрия - в основу классической механики Ньютона.
Современники рисуют Гаусса жизнерадостным человеком, наделенным большим чувством юмора. Гаусс живо интересовался литературой, философией, политикой, экономикой. Его внимание привлек расцвет культуры России начала XIX в. Он поддерживал научные связи с Петербургской академией наук, которая еще в 1801 г. избрала его своим членом-корреспондентом, а в. 1824 г.- иностранным членом. В возрасте 62 лет Гаусс выучил русский язык и в своих письмах в Петербургскую академию наук жаловался на недостаток русской литературы в Гёттингене, просил присылать ему русские журналы и книги, в частности «Капитанскую дочку» Пушкина.
Умер Гаусс в 1855 г.
У него было немного личных учеников. Однако его можно с полным правом назвать учителем математиков всего мира. Истоки основных идей современной алгебры, геометрии, теории чисел и высшего анализа восходят к Гауссу. Созданными им понятиями и методами до сих пор оперируют математики и физики.
Николай Иванович Лобачевский - великий математик, «Коперник в геометрии», построивший новую систему геометрии, родился в 1792 г. в Нижнем Новгороде (теперь Горький). Отец его умер рано, и мать, умная и энергичная женщина, переехала со своими тремя) сыновьями в Казань. Она добилась того, чтобы ее дети были приняты в гимназию на казенный счет. По окончании гимназии все трое продол-
жали учение в незадолго до того открывшемся Казанском университете. Николай поступил на физико-математический факультет, когда ему было только 14 лет. К этому времени он овладел уже латинским, французским и немецким языками настолько, что мог свободно читать научную литературу и углубляться в изучение трудов Л. Эйлера, Ж. Лагранжа, К. Гаусса. Его руководителем в университете был профессор Бартельс, ученый с большим научным кругозором, которому до того выпала честь быть учителем другого крупнейшего математика- Гаусса. Бартельс вскоре обратил внимание на математическое дарование Лобачевского и побуждал его к самостоятельным научным исследованиям.
Однако инспекторы Казанского университета были недовольны молодым Лобачевским. Они заметили у юноши признаки вольнодумства и даже «признаки безбожия». Лобачевскому грозило исключение из университета и отдача в солдаты. Только энергичное заступничество профессоров спасло юношу.
В 1811 г. Лобачевский был произведен, минуя степень кандидата, в магистры, а в 1814 г. приступил к чтению лекций. Через два года он получил кафедру чистой математики и стал профессором университета. В течение более тридцати лет он читал все основные курсы математики, а часто - механики и астрономии. В 1827 г. его выбрали ректором Казанского университета. С этого времени Лобачевский бессменно руководил университетом вплоть до своей отставки в 1846 г. Он оказался не только замечательным педагогом, но и прекрасным организатором: при нем были построены астрономическая и магнитная обсерватории, анатомический театр, химическая лаборатория, физический кабинет и библиотека. Лобачевским были основаны и знаменитые «Ученые записки» Казанского университета.
Лобачевскому принадлежит ряд первоклассных работ по алгебре и математическому анализу. Но главным содержанием его жизни было создание и пропаганда неевклидовой геометрии. Евклид построил свою геометрию в III в. до н. э. (см. статьи «Как возникла геометрия» и «О различных геометриях»).
Лобачевский, как и его предшественники, сначала пытался доказать аксиому о параллельных. Но уже в 1823 г. у него зародилась новая идея: он пришел к мысли, что аксиому о параллельных Евклида вообще нельзя доказать, более того, можно принять другую аксиому о параллельных и на ее основе построить
492
новую, неевклидову геометрию, столь же стройную и непротиворечивую, как и геометрия Евклида. И Лобачевский с увлечением принялся за построение этой новой системы, исследуя и доказывая ее законы (см. те же статьи).
Нам трудно сейчас представить, насколько смелой была мысль Лобачевского. Ведь на протяжении двух тысяч лет геометрия Евклида казалась единственно возможной, столь же естественной, как законы сложения целых чисел. На ее основе строилась классическая механика Ньютона да и вся классическая физика. Нужно было большое личное мужество, беззаветная преданность научной истине, чтобы не побояться выступить с утверждением о возможности новой геометрии. Такое утверждение многим казалось тогда равносильным безумию.
11 февраля 1826 г. на заседании отделения физико-математических наук Лобачевский сделал доклад, в котором изложил свои новые идеи в геометрии. Эта дата считается днем рождения неевклидовой геометрии. Текст доклада не сохранился. Позднее Лобачевский писал, что в этом своем докладе он развивал мысль о том, что аксиома о параллельных не может быть доказана, установить же ее выполнимость в нашем реальном физическом пространстве можно только путем наблюдений. По-видимому, смелые мысли Лобачевского вызвали глубокое недоумение. Но это не обескуражило молодого ученого. В 1829 -1830 гг. он опубликовал труд «О началах геометрии», в котором подробно излагал геометрию, основанную на новой аксиоме о параллельных, согласно которой через точку, лежащую в данной плоскости вне данной прямой, можно провести по крайней мере две прямые, не пересекающие заданную прямую. Но и это сочинение Лобачевского встретило пренебрежение и насмешки. Полагая, что он все еще недостаточно ясно изложил свои идеи, Лобачевский в 1835 г. пишет новый труд «Воображаемая геометрия», затем издает французский перевод его, вслед за этим - «Новые начала геометрии с полной теорией параллельных» и, наконец, «Геометрические исследования с полной теорией параллельных» на немецком языке.
Лобачевский был глубоко убежден, что его система получит применение для описания и изучения свойств нашего пространства. Желая проверить, какие геометрические законы имеют место в космосе, он подсчитал по данным астрономических наблюдений сумму углов треугольника, вершинами которого являются два диаметрально противоположных положения Земли на своей орбите и звезда Сириус. Известно,
Николай Иванович Лобачевский.
что в евклидовой геометрии сумма углов любого треугольника равна 2d, в геометрии же Лобачевского эта сумма различна у разных треугольников, но всегда <2 d. Лобачевский надеялся, что у такого громадного треугольника, который он выбрал, отклонение суммы углов от 2 d будет значительным. Однако расчет показал, что отклонение это очень незначительно - оно могло быть объяснено погрешностями при наблюдении.
Геометрия Лобачевского так и не получила признания при жизни великого геометра. В 1846 г. исполнилось 30 лет профессорской деятельности Лобачевского, и он, по законам того времени, должен был уйти в отставку. Ему очень тяжело было покинуть любимый университет, и свою отставку он пережил болезненно. Мысль о том, что его геометрия все еще не находит признания, также угнетала Лобачевского. В последние годы жизни он решил еще раз изложить свои идеи и принялся за «Пангеометрию», в которой стремился особенно ясно
493
оттенить мысль о том, что евклидова геометрия - частный, предельный случай более общей неевклидовой геометрии. В это время он почти полностью потерял зрение, и ему приходилось диктовать свою книгу ученикам. Все необходимые выкладки он производил в уме. Книгу ученый закончил за год до смерти, наступившей в 1856 г.
Глубоко трагична судьба этого замечательного человека, так и не дождавшегося признания своего великого открытия.
Прошло не более 15 лет со дня смерти Лобачевского, и геометрия его была не только признана, но и вошла в моду. О ней читались лекции и писались трактаты, велись научные дебаты и салонные разговоры, ей посвящались популярные книги и стихи. Такой успех можно сравнить только с успехом теории относительности в 20-х годах нашего века или «думающих» машин и кибернетики в наши дни.
Начиная с 60-х годов прошлого века неевклидова геометрия приобретала все большее значение в математике. Огромную роль сыграло то обстоятельство, что в трудах позднейших ученых была доказана непротиворечивость новой геометрии. Только после этого она сделалась полноправной математической теорией. Действительно, при построении новой геометрии Лобачевский исходил из тех же аксиом, что и Евклид, только принял вместо евклидовой аксиомы о параллельных новую аксиому, которую мы привели выше. Предложения геометрии Лобачевского получались как следствия этой новой системы аксиом. При этом могло случиться, что, развивая эти следствия дальше, мы на каком-то шагу придем к противоречию. Это означало бы, что принятое допущение, т. е. аксиома о параллельных Лобачевского, неверна. Таким образом, мы получили бы доказательство аксиомы Евклида методом от противного. Если же противоречие никогда не получится, то, следовательно, построенная система геометрии логически равноправна евклидовой.
В связи с неевклидовой геометрией впервые был поставлен вопрос о том, как вообще можно доказать непротиворечивость некоторой математической теории, и были найдены первые методы доказательства непротиворечивости. Исследование этой новой проблемы имело большое значение для всего дальнейшего развития математики. Прежде всего возникла необходимость выявить и проанализировать все аксиомы, которые лежат в основе геометрии Евклида. Это было сделано крупнейшим математиком Д. Гильбертом в конце XIX в. Дальнейшее изучение этих проблем привело к созданию аксиоматического метода, играющего важнейшую роль в современной математике.
В конце XIX в., как и предвидел Лобачевский, его геометрия получила применение в физике, а именно в специальном принципе относительности. Для общего принципа относительности оказались необходимыми другие системы неевклидовой геометрии, построенные Б. Риманом.
Таким образом, геометрия Лобачевского не только необыкновенно расширила предмет самой геометрии, она получила широкое применение в других областях математики, способствовала рождению новых математических идей и методов и оказалась незаменимой для современной физики.
Короткой, но яркой была жизнь этого замечательного математика, идеи которого преобразовали всю алгебру и оказали решающее влияние на развитие геометрии и анализа.
Галуа родился 26 октября 1811 г. близ Парижа в небольшом городке Бур-ля-Рен. Отец его руководил учебным заведением для юношей, а с 1813 г. был бессменным мэром своего города. Эварист рос болезненным и впечатлительным мальчиком. Первоначальное образование он получил под руководством своей матери, большой поклонницы античной культуры. Двенадцати лет Галуа поступил в Королевский коллеж в Париже. Первые три года он считался хорошим учеником, хотя учителя и отмечали его «несколько необычные манеры», но на четвертом году он начал заниматься математикой и так увлекся ею, что потерял интерес к другим наукам. По выражению одного из педагогов, «он был одержим демоном математики».
Галуа самостоятельно изучал сочинения Ж. Лагранжа, Л. Эйлера, К. Гаусса, а впоследствии и высоко ценимого им Н. Абеля. В 1828 г. Эварист потерпел неудачу на конкурсных экзаменах в Политехническую школу и целый год упорно работал над углублением своих математических знаний под руководством прекрасного педагога Ришара. В это же время у Ришара занимались будущий знаменитый математик Ш. Эрмит и будущий известный астроном У. Леверье, но самым одаренным из своих учеников Ришар считал Галуа. Уже в это время была опубликована одна из работ Галуа. И тем
494
не менее, к большому удивлению своих товарищей и Ришара, в 1829 г. Галуа снова провалился на конкурсных экзаменах. На этот раз, по-видимому, решающую роль сыграл неуравновешенный характер Эвариста. Ему показалось, что экзаменаторы смеются над ним: задают ему слишком простые вопросы. Придя в ярость, Галуа отказался отвечать.
Если бы Галуа поступил в Политехническую школу, быть может, вся его жизнь сложилась бы иначе. В то время в Политехнической школе преподавали лучшие математики Франции и учащиеся имели полную возможность заниматься научными исследованиями. Но Эварист не мог ждать еще год. Отец его умер, и ему надо было заботиться о средствах для существования. Поэтому, по совету Ришара, он поступил в Нормальную школу, которая давала стипендию и готовила преподавателей для высших и средних учебных заведений. За год пребывания в этой школе Галуа написал несколько научных работ, из которых одна, посвященная вопросам теории чисел, представляла исключительный интерес. Эти работы вместе с первым исследованием о решении уравнений в радикалах он представил на соискание Большой математической премии Парижской академии наук. Все статьи попали к непременному секретарю академии знаменитому математику Ж. Фурье. Однако Фурье вскоре умер, в его бумагах нашли только часть работ Галуа, другая часть, в том числе исследование о разрешимости уравнений в радикалах, была утеряна. Найденные работы были опубликованы.
До июля 1830 г. Галуа мало интересовался политикой. Но с первых же дней Июльской революции, с присущей ему страстностью, Эварист бросился в самую гущу политических событий. Он примкнул к левому крылу республиканский партии - Обществу друзей народа. В декабре того же года за разоблачение в печати двуличного поведения директора Нормальной школы в дни Июльской революции Галуа был исключен из этой школы.
В январе 1831 г. Галуа вновь передал в Парижскую академию наук рукопись своего исследования о решении уравнений в радикалах. В письме президенту академии Галуа просил «по крайней мере» прочесть со вниманием то, что он написал. На этот раз работа была передана на рассмотрение двум академикам. Однако они не смогли понять рукописи Галуа - слишком новы были изложенные там идеи. Академия отвергла работу Галуа. В это время Галуа был в тюрьме. Его арестовали в мае 1831 г. за то,
Эварист Галуа.
что он произнес тост, который все восприняли как призыв к свержению короля Людовика Филиппа. Суд оправдал Эвариста, но вскоре после освобождения он вновь был арестован как один из вожаков демонстрации 14 июля. На этот раз он просидел в тюрьме около 9 месяцев. Вскоре после освобождения жизнь юноши оборвалась. В мае 1832 г. двадцатилетний Эварист Галуа был убит на дуэли.
В ночь перед дуэлью, зная уже, что его работы отвергнуты академией, и уверенный в правильности своих выводов, Галуа написал своему другу, Огюсту Шевалье, письмо, почти целиком посвященное математике. Он сформулировал в нем свои основные теоремы, относящиеся к теории уравнений. Он просил Шевалье в случае своей смерти обратиться публично к К. Гауссу или К. Якоби с просьбой «дать заключение не о справедливости, а о важности этих теорем».
Однако и это письмо, и замечательная работа Галуа «Об условиях разрешимости уравнений в радикалах» пролежали еще 14 лет. Они были опубликованы вместе с другими сохранившимися работами Галуа только в 1846 г. известным
495
ученым Ж. Лиувиллем. Но прошло еще около 20 лет, прежде чем идеи Галуа прочно вошли в математическую науку.
Математическое наследство Галуа составляет всего шестьдесят небольших страниц печатного текста. Многие свои мысли он не успел изложить, сохранились лишь наброски неоконченных работ и планы, но то, что он успел сделать, настолько велико, что совершенно изменило лицо алгебры.
Проблема, которую решал Галуа, состояла в следующем: известно, что корни уравнений 2-й, 3-й, 4-й степеней можно выразить с помощью радикалов через коэффициенты этих уравнений. В 1824 г. Абель доказал, что существуют уравнения 5-й степени, которые в радикалах не решаются. Между тем было известно, что можно найти уравнения любой степени, разрешимые в радикалах, например уравнения хn -1=0 при n = 2, 3, 4,,.. Пусть теперь задано уравнение n - й степени, т. е. заданы его коэффициенты. Как узнать, решается ли оно в радикалах? Эту проблему и решил Галуа. Основной интерес представляет метод его решения. К сожалению, мы сможем здесь сказать о нем очень мало. Разве только то, что Галуа построил для решения задачи аппарат теории групп и начал строить теорию полей. Обе эти теории являются основой современной алгебры, а теория групп - и всей математики. (См. статью «Чем занимается алгебра?».)
Пафнутий Львович Чебышев, один из крупнейших математиков прошлого века, родился в 1821 г. в Калужской губернии в имении отца. Первоначальное образование он получил дома. Шестнадцати лет Чебышев был принят на физико-математический факультет Московского университета. Здесь он написал свою первую научную работу «Вычисление корней уравнения», в которой анализировал все до того существовавшие методы приближенного вычисления корней алгебраических уравнений: способы Ньютона, Лагранжа, Фурье, и предлагал свой собственный, наиболее общий, из которого все предыдущие получаются как частные случаи. За эту работу Чебышев был награжден серебряной медалью.
В 1841 г. Чебышев окончил Московский университет. Ему предстояло сделать выбор: либо идти на службу и бросить математику, либо целиком отдаться занятиям любимой наукой и терпеть лишения. Чебышев выбрал последнее.
В 1846 г. он защитил магистерскую диссертацию «Опыт элементарного анализа теории вероятностей». В следующем году Чебышев переехал в Петербург, где ему предложили должность адъюнкта в Петербургском университете. С 1860 г. он стал профессором того же университета. Много сил потратил Чебышев на то, чтобы систематизировать и издать исследования Эйлера по теории чисел. Вопросы этой теории все более и более приковывали внимание самого Чебышева. В 1849 г. он защитил докторскую диссертацию «Теория сравнений», посвященную теоретико-числовым проблемам. К этому же времени относятся знаменитые работы Чебышева о простых числах.
Еще в глубокой древности ученых интересовал вопрос о том, по какому закону расположены в натуральном ряду простые числа: 2, 3, 5, 7, 11, 13, 17, 19, ... В «Началах» Евклида было доказано, что простых чисел бесконечно много. Хотя со времен Евклида прошло более двух тысяч лет, к его теореме ничего нового добавлено не было. Простые числа в натуральном ряду располагаются чрезвычайно прихотливо. С одной стороны, существуют простые числа-«двойники», которые отличаются одно от другого на 2, например 3 и 5, 7 и 9, 11 и 13, 17 и 19, 41 и 43 и т. д. Имеется гипотеза, что таких «двойников» бесконечно много. С другой стороны, если расположить все простые числа в ряд в порядке их возрастания:
p1 , p2 , pn ,... (p1 < p2 < ...< pn <...),
то можно всегда найти в этом ряду два соседних числа pm и pm+1, разность между которыми pm +1 - pm как угодно велика.
Поставим теперь такую задачу. Пусть p (n) - число простых чисел, не превосходящих п. Мы не можем точно определить, каково будет p (n) для любого n ; но нельзя ли его вычислить приближенно? Еще К. Гаусс и А. Лежандр, занимаясь этим вопросом, чисто эмпирически пришли к выводу, что p (n) для больших n приближенно равно n /log e n, причем в знаменателе стоит натуральный логарифм, т. е. взятый по основанию е=2,7182... Но даже такие математики не смогли доказать замеченного ими факта. Только Чебышеву удалось сдвинуть проблему
496
о простых числах с мертвой точки. Он показал, что если отношение (p (n)/ n)/log e n при n, неограниченно возрастающем, имеет предел, то этот предел равен единице. Впоследствии было показано, что этот предел существует, это означает, что при больших n числитель p (n) примерно равен знаменателю n/loge n .
Исследования Чебышева по теории чисел сразу же выдвинули молодого русского математика в число первых ученых Европы.
Второй цикл работ, прославивших Чебышева, составили его исследования по теории вероятностей. Теория вероятностей - сравнительно молодая область математики. Первые задачи ее появились только в XVI - XVII вв. и были связаны с азартными играми (в кости, карты), а впоследствии - с обработкой результатов наблюдений. И хотя многие ее основные предложения ко времени Чебышева были уже хорошо известны, методы этой теории были лишены должной строгости, а приложения ее часто приводили к явно ошибочным результатам. Такие неудачи привели к разочарованию в теории вероятностей, некоторые говорили даже о «математическом скандале».
Только Чебышев сумел вывести теорию вероятностей из кризиса. Он ввел и систематически рассматривал случайные величины, а также нашел новый метод доказательства теорем этой теории. С этого времени теория вероятностей стала полноправной математической дисциплиной.
Чебышев является основателем русской школы теории вероятностей, которая и до сих пор занимает ведущее место в мировой науке. Благодаря работам Чебышева и его школы теория вероятностей сделалась могучим орудием для исследования проблем физики (особенно квантовой механики), техники, биологии и других областей знания.
Еще в юности Чебышев любил строить сложные механизмы. Эта любовь сохранилась у него на всю жизнь. Ученый изобрел более 40 типов шарнирных (или суставчатых, как он их называл) механизмов. Среди них были стопоходящая машина, воспроизводящая движения животных при ходьбе, гребной механизм, который повторял движение весел лодки, самокатное кресло и многие другие. Выставка этих механизмов, устроенная при жизни великого ученого в Чикаго, произвела потрясающее впечатление на современников. Чебышев построил
Пафнутнй Львович Чебышев.
также арифмометр-полуавтомат, который хранится в Париже в Музее искусств и ремесел. Однако Чебышев интересовался механизмами не только как изобретатель, но и как математик. Занимаясь теорией механизмов, он сумел увидеть в ней новые математические проблемы, которые в его время были еще совершенно не изучены. Его работы, посвященные этим проблемам, положили начало теории наилучшего приближения функций. Эта теория с тех пор успешно развивается.
Чебышев как-то в шутливой форме высказал мысль, что в своем развитии математика прошла три периода. В первом - задачи ставили боги (он имел в виду задачу удвоения куба, постановка которой по древнегреческому преданию приписывалась оракулу), во втором - полубоги (т. е. такие математики, как П. Ферма), в наступившем третьем периоде задачи ставит нужда, т. е. жизнь. К требованиям практики и был особенно чуток Чебышев. В ней умел он находить новые математические задачи, решение которых доводил до получения окончательного числового результата, с тем чтобы вновь применить его на практике.
497
У П. Л. Чебышева было много учеников. Он по праву считается основателем Петербургской математической школы, которая насчитывает в своих рядах таких первоклассных ученых, как Е. И. Золотарев, А. А. Марков, А. М, Ляпунов, Г. Ф. Вороной и др.
Заслуги П. Л. Чебышева были признаны всем ученым миром. В 38 лет он был избран членом Петербургской академии наук, затем членом Парижской и Берлинской академий, Лондонского королевского общества и многих других академий.
Ученый прожил долгую жизнь и до последней минуты много и плодотворно работал. Умер Чебышев в 1894 г. За письменным столом он внезапно почувствовал себя плохо и вскоре скончался от паралича сердца.
Имя первой русской женщины-математика Софьи Васильевны Ковалевской известно всему образованному миру. Рассказ о ее жизни - это увлекательная история о том, как маленькая жизнерадостная девочка, «воробышек», стала выдающимся математиком; это поучительная история о девушке, полюбившей свободу и математику; это история о женщине-герое, проложившей дорогу в науку, к высшему образованию женщинам России и Европы.
Она родилась в 1850 г. в Москве в богатой семье генерал-лейтенанта артиллерии в отставке В. В. Корвина-Круковского. Маленькая Соня училась удивительно легко. Отец всячески поддерживал и развивал ее интерес к науке. Любознательная и настойчивая в учебе, Соня особенно увлеклась математикой. Любопытно, как произошло ее первое знакомство с высшей математикой. Случилось так, что стены в детской комнате были оклеены лекциями по математическому анализу знаменитого академика М. В. Остроградского. Как пишет С. В. Ковалевская, «от долгого ежедневного созерцания внешний вид многих из формул так и врезался в моей памяти», и через много лет ее преподаватель по математическому анализу удивлялся, «как скоро она охватила и усвоила себе понятие о пределе и производной, точно она их наперед знала». Особенно возбуждали фантазию девочки математические рассуждения ее дяди, «внушая ей благоговение к математике, как науке высшей и таинственной, открывающей перед ней новый чудесный мир, недоступный простым смертным». Знакомый отца, профессор Тырнов, обратил внимание родителей на математические способности четырнадцатилетней девочки.
Еще не зная тригонометрии, Соня пыталась разобраться в смысле тригонометрических формул, встретившихся ей в учебнике по физике. Отец пригласил заниматься с дочерью известного преподавателя, и с 15 лет она начала систематически изучать курс высшей математики.
В то время в России девушкам было запрещено учиться в университетах и высших школах. Женщины могли поступать только в некоторые зарубежные университеты. Но уехать из-под строгого надзора родителей молодым девушкам было очень трудно. Многим девушкам из богатых семей приходилось вступать в фиктивный брак, чтобы получить право уехать за границу и там учиться. Софья Васильевна вступила в такой брак с молодым ученым В. О. Ковалевским.
В 1869 г. молодые супруги уезжают за границу, в Германию, в университетский городок Гейдельберг. Каждый из них принялся усердно заниматься своими науками.
В Гейдельберге Ковалевская посещала лекции крупнейших ученых-математиков. В 1870 г. она переезжает в Берлин, решив добиться права на посещение лекций знаменитого немецкого математика К. Вейерштрасса. Вейерштрасс читал лекции в Берлинском университете, куда женщины не допускались. Сам Вейерштрасс считал, что в университете, а особенно на математическом факультете, женщинам учиться нельзя. Однако Ковалевская добилась того, чтобы Вейрштрасс проэкзаменовал ее на право быть его частной ученицей. Вейерштрасс предложил ей задачи, которые сам считал трудными для таких экзаменов. Каково же было удивление профессора, когда на следующий день взволнованная молодая женщина принесла ему блестяще решенные задачи! Вскоре Вейерштрасс признал особое математическое дарование своей ученицы. Он писал: «Что касается математического образования Ковалевской, то я имел очень немного учеников, которые могли бы сравниться с ней по прилежанию, способностям, усердию и увлечению наукой».
Через 4 года по ходатайству Вейерштрасса в Геттингенском университете С. В. Ковалевской заочно присуждается ученая степень доктора философии. (Эту ученую степень присуждали
498
за выдающиеся заслуги в математике, физике и химии.) Это была достойная награда за выдающиеся математические труды, написанные ею за это время. Работы были посвящены интереснейшим вопросам математики и механики. Работа «К теории дифференциальных уравнений в частных производных» содержит доказательство существования решений у таких уравнений. В курсах дифференциальных уравнений, которые теперь читают в университетах, эта теорема называется теоремой Ковалевской. Другая работа посвящена исследованию формы гигантского кольца, окружающего планету Сатурн, проведенному, как говорится, «на кончике пера». В третьей работе излагаются труднейшие теоремы математического анализа.
Двадцати четырех лет, «с докторским дипломом в кармане», Ковалевская возвращается в Петербург. Ее личная и научная жизнь сложилась так, что она отошла от занятий математикой. По существовавшим законам она, как женщина, имела право преподавать только арифметику в младших классах. В это время Софья Васильевна начинает писать статьи и рассказы, начинается ее литературная деятельность. Сама Ковалевская писала, что она всю жизнь не могла решить, к чему у нее было «больше склонности - к математике или к литературе». Среди ее знакомых не только ученые - Д. И. Менделеев и П. Л. Чебышев, но и писатели - Ф. М. Достоевский и И. С. Тургенев. Достоевский, несомненно, во многом способствовал пробуждению литературного таланта у Ковалевской. Ее перу принадлежат «Воспоминания детства», «Нигилистка», драма «Борьба за счастье» и многие другие произведения.
В 1883 г. трагически погиб В. О. Ковалевский. После неоднократных приглашений С. В. Ковалевская соглашается работать в Стокгольмском университете. Здесь начинается расцвет ее научной и литературной деятельности. В Стокгольмском университете Ковалевская прочла с большим успехом около двадцати курсов по математике. Написанная ею научная работа о вращении твердого тела была удостоена особой премии Парижской академии наук, причем сумма премии была увеличена с 3000 франков до 5000.
Софья Васильевна Ковалевская.
В 1889 г. Петербургская академия наук, по настоянию П. Л. Чебышева, предварительно приняв специальное постановление о присуждении женщинам академических званий, избрала С. В. Ковалевскую своим членом-корреспондентом. Сохранилась телеграмма, в которой ей сообщалось об этом событии: «Наша Академия наук только что избрала Вас членом-корреспондентом, допустив этим нововведение, которому не было до сих пор прецедента. Я очень счастлив видеть исполненным одно из моих самых пламенных и справедливых желаний. Чебышев».
Умерла С. В. Ковалевская в 1891 г. внезапно, в расцвете творческих сил.
499
Выдающийся французский математик С. Пуассон, будучи подростком, вначале проявлял во всем крайне ограниченные способности. Но после того как самостоятельно придумал искусное решение старинной задачи о дележе вина на две равные части при помощи двух пустых сосудов неодинаковой вместимости, он увлекся математикой и избрал ее своей специальностью.
Аналогичный «толчок» привел в математику профессора Московского университета И. И. Чистякова. В одном из своих выступлений (в 1911 г.) И. И. Чистяков рассказал о себе, что он пристрастился к математике с того момента, как еще подростком самостоятельно решил такую задачу: «Доказать, что всякое простое число начиная с пяти, будучи увеличено либо уменьшено на 1, делится на 6».
Намереваясь показать людям, что двоичное счисление - это не забава, а метод с большим будущим, знаменитый немецкий математик Г. Лейбниц изготовил специальную медаль. На ней изображена таблица простейших действий над числами в двоичной системе и отчеканена фраза: «Чтобы вывести из ничтожества все, достаточно единицы».
В восточной части Амстердама есть улицы Пифагора, Архимеда, Ньютона и Коперника.
Французскому ученому Б. Паскалю (1623-1662) было 12 лет, когда он написал математический «Трактат о звуках».
Ответ к стр.395. b =а+с
Решение к стр.395.
Пусть одна дробь a/b, а другая ka/b
тогда, по условию,
a² /b² (1+ k² )= a³ /b³ (1+ k³ ), или
1+ k² = a/b (1 + k³),
откуда,
a/b=(1+k²)/(1+k³) Полагая k =2, получаем:
a/b =5/9
и, следовательно,
(5/9)² +(10/9)² =(5/9)³ +(10/9)³ .
Полагая k = 3, получаем:
a/b=(1+9/(1+27)=5/14 и, следовательно,
(5/14)² +(25/14)² =(5/14)³ +(15/14)³
и т. д. Конечно, k можно давать и дробные значения, например, для
k=3/2 получим
а/ b=26/35.
Решение к стр.439.
1. а) В пятеричной системе; б) в четверичной системе; в) в восьмеричной системе; г) в двоичной системе.
2. Отдельно числитель и знаменатель дроби 3/7 переведены в двоичную систему, а затем выполнено деление числителя на знаменатель следующим образом:
3. Ясно, что
2 n < 1 000 000 000 < 2 n+1.
Теперь надо положить n + 1 = 30 и убедиться в справедливости записанных неравенств. Можно также найти n, применяя логарифмирование записанных неравенств. Тогда получим более простые неравенства:
n lg 2 < lg109 < (n+1) lg2, или
n < 9 ⁄ lg2 < n+1,
n < 9 ⁄ 0,3010 < n+1,
n < 29,9 < n + 1.
Так как n - число натуральное, то n = 29 и, следовательно, для записи одного миллиарда в двоичной системе надо употребить n + 1 = 30 цифр.
500
Точно датировать возникновение важнейших понятий - целого числа, величины, фигуры - невозможно. Когда возникла письменность, представление о них уже сложилось. К этому времени были выработаны и различные системы письменной нумерации целых чисел.
2000-1700 гг. до н. э. - первые дошедшие до нас математические тексты: два египетских папируса и многочисленные глиняные таблички из древнего Вавилона, содержащие формулировки и решения задач. Египтяне пользовались десятичной непозиционной нумерацией и дробями с числителем 1 («основные» дроби). У вавилонян была шестидесятеричная позиционная система счисления без нуля и систематические шестидесятеричные дроби. Позднее, в середине первого тысячелетия до н. э., вавилоняне ввели знак для обозначения пропущенного шестидесятеричного разряда. Геометрия в Вавилоне и в Египте была по преимуществу вычислительной. Так, были известны правила вычисления площадей треугольника по стороне и высоте, круга по его радиусу (вавилоняне брали при этом в качестве p число 3, а египтяне число 3,16), а также объем пирамиды и усеченной пирамиды с квадратным основанием. Вавилоняне знали, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов, а также обратное предложение. По-видимому, оба эти предложения были открыты ими на примерах и доказывать их в общем виде они еще не умели.
Наиболее замечательное достижение этого периода - создание в древнем Вавилоне элементов алгебры и открытие правила решения квадратных уравнений. Вавилоняне умели также находить приближенные значения квадратных корней из неквадратных чисел. Им были известны формулы суммы арифметической прогрессии и суммы квадратов натурального ряда.
Математические знания излагались в эту эпоху в виде рецептов, правильность которых не доказывалась; обычно приводились однотипные числовые примеры и их решения. Математики как науки еще не было.
VI в. до н. э. - систематическое введение логических доказательств, явившееся переломным моментом в развитии математики. В Пифагорейской научной школе было начато построение геометрии как отвлеченной науки, истины которой выводятся из немногих исходных аксиом с помощью доказательств. К пифагорейцам восходят первые математические теории: планиметрия прямолинейных фигур (включая строгое доказательство знаменитой теоремы Пифагора) и элементы теории чисел (введение понятий простого числа, взаимно простых чисел, исследование теории делимости, построения совершенных чисел). В этой же школе были открыты четыре из пяти правильных тел: куб, тетраэдр, октаэдр и додекаэдр.
V в. до н. э. -в Пифагорейской школе сделано величайшее открытие о несоизмеримости стороны квадрата и его диагонали. Оно показало, что рациональных чисел (т. е. целых чисел и дробей) недостаточно для измерения геометрических величин и обоснования учения о подобии. Благодаря этому открытию возникла необходимость создания теории отношений как соизмеримых, так и несоизмеримых геометрических величин.
V в. до н. э. (вторая половина) - создана так называемая геометрическая алгебра, которая давала возможность в общем виде решать задачи, сводящиеся к квадратному уравнению или последовательности таких уравнений, чисто геометрически, с помощью циркуля и линейки. Геометрическая алгебра играла в античной математике роль нашей буквенной алгебры, но аппарат ее был гораздо менее удобен.
В это же время были сформулированы три знаменитые задачи древности: 1) удвоение куба (построить куб, имеющий объем в два раза больший данного), 2) трисекция угла (разделить произвольный угол на
501
три равные части) и 3) квадратура круга (построить квадрат, равновеликий данному кругу). Все эти построения, как было доказано в XIX в., невозможны с помощью циркуля и линейки. Древние использовали для их решения новые кривые: конические сечения (эллипс, гиперболу и параболу) и квадратрису (первую трансцендентную кривую).
В поисках квадратуры круга Гиппократ Хиосский открыл квадрируемые луночки (получившие название гиппократовых), т. е. фигуры, ограниченные дугами окружностей, для которых можно построить равновеликие им квадраты.
В конце V в. Гиппократ составил первые «Начала» - систематическое изложение основ математики своего времени. Труд этот до нас не дошел.
IV в. до н. э. (первая половина) - афинский математик Теэтет предпринял исследование алгебраических иррациональностей и начал классификацию их. Он определил простейшие классы квадратичных иррациональностей, такие, как √‾a, √‾a + √‾b,
√‾( √‾a + √‾b), √‾ab, √‾( √‾ab) ,..., которые были впоследствии описаны в «Началах» Евклида. Он показал также, что³ √‾а иррационален, если а не является кубом.
IV в. до н. э. (середина) - великий математик и астроном древности Евдокс из Книда создает общую теорию отношений для любых однородных величин (как соизмеримых, так и несоизмеримых). Эта теория совпадает по существу с теорией действительных чисел, предложенной в конце XIX в. Р. Дедекиндом. Для определения площадей и объемов Евдокс разработал так называемый метод исчерпывания. В основе обеих теорий лежало общее учение о величинах. Величины определялись аксиоматически, причем впервые была сформулирована важнейшая аксиома, известная ныне под названием аксиомы Архимеда: если а > b , то можно повторить b столько раз, что nb> а. С помощью новых методов Евдокс впервые доказал, что конус равновелик 1/3 цилиндра, имеющего одинаковые с ним основания и высоту, а пирамида равновелика 1/3 соответствующей призмы. Он доказал также, что площади двух кругов относятся как квадраты их диаметров.
300 г. до н. э. -Евклид создает свои «Начала», в которых подводит итог всему предшествующему развитию античной математики. Метод изложения «Начал» получил название дедуктивного и стал образцом для построения математической теории. В «Началах» не только впервые систематически излагалась геометрия, но и элементы теории чисел, алгебры, теория отношений и метод исчерпывания. Здесь формулировался алгоритм Евклида для нахождения наибольшего общего делителя двух чисел, доказывалось, что произведение двух простых чисел pq не может делиться ни на какое третье простое число, а также устанавливалось, что простых чисел бесконечно много. В «Началах» впервые встречается строгий вывод формулы суммы конечного числа членов геометрической прогрессии и показывается, что существует только пять правильных тел: куб, тетраэдр, октаэдр, додекаэдр и икосаэдр - и никаких других правильных тел нет.
III в. до н. э. - Архимед разрабатывает методы нахождения площадей и объемов, а также методы определения касательных и наибольших и наименьших значений величин, которые он применил для решения проблем статики, гидростатики и теории равновесия плавающих тел (см. стр. 472-474). Методы Архимеда легли в основу дифференциального и интегрального исчисления, созданного в XVII в.
III - II вв. до н. э. - Аполлоний систематически и всесторонне исследует конические сечения, развивая методы как аналитической, так и проективной геометрии. Его книги о конических сечениях послужили основой для создания аналитической геометрии Р. Декартом и П. Ферма (XVII в.), проективной геометрии Б. Паскалем и Ж. Дезаргом (XVII в.), а также явились математическим аппаратом при исследованиях по механике и астрономии И. Кеплера, Г. Галилея и И. Ньютона.
I - II вв. н. э. - широкое развитие вычислительно-алгебраических методов в античной математике.
I в. (конец) - Менелай создает систематический курс сферической геометрии, построенный по образцу «Начал» Евклида, и развивает сферическую тригонометрию.
Во II в. Птолемей в своих астрономических трудах излагает плоскую и сферическую тригонометрию; он выводит формулу, равносильную
sin ( a + b) = sin a cos b + cos a sin b ,
и составляет подробные таблицы хорд (вместо линии синуса древние рассматривали всю хорду). В таблицах Птолемей употреблял символ для обозначения пропущенного шестидесятеричного разряда. Возможно, что этот символ и явился прообразом нуля.
III в. н. э. - Диофант Александрийский, последний великий математик древности, пишет «Арифметику», в которой формулирует общие правила алгебры: правило переноса членов из одной части уравнения в другую и правило приведения подобных членов, а также правило умножения многочлена на многочлен, причем отмечает, что «вычитаемое на вычитаемое дает слагаемое». В этой книге впервые в истории науки вводится алгебраическая символика для обозначения неизвестного и первых его положительных и отрицательных степеней вплоть до шестой, а также для равенства и вычитания. Диофант развивает учение о решении неопределенных уравнений с целыми коэффициентами в целых или рациональных числах. Эти уравнения получили в современной математике название диофантовых.
II в. до н. э. - создание древнейшего дошедшего до нас китайского математического трактата «Математика в девяти книгах», содержащего сведения по арифметике и геометрии. При решении задач в трактате применяется теорема Пифагора. Наиболее замечательным является единообразный метод решения системы линейных уравнений. При этом появляются отрицательные числа, для которых формулируются правила сложения и вычитания. В трактате излагается также алгоритм вычисления квадратных и кубических корней, аналогичный современному. Этот алгоритм в VII - XIII вв. был перенесен на случай вычисления корней общих уравнений третьей и четвертой степеней. Он совпадает в основном с так называемой схемой Горнера, полученной в Европе в XIX в.
502
Ill в. н. э. -в трактате Сунь Цзы встречаются именованные десятичные дроби.
V - VI вв. - создание в Индии десятичной позиционной системы счисления и введение в нее нуля как особой цифры.
499 г. - в астрономическом трактате Ариабхатты решается в целых числах неопределенное уравнение
ax + by = c.
Около 628 г. - индийский астроном Брахмагупта, свободно оперируя отрицательными числами, дает единое правило для решения любого квадратного уравнения. Он же формулирует правила действий с нулем, который благодаря этому становится числом, равноправным с другими числами. Брахмагупта знал способ решения неопределенного уравнения ах² +1= y²
в целых числах. Обоснование этого метода было дано Л. Эйлером и Ж. Лагранжем в XVIII в. Брахмагупта широко пользовался алгебраической символикой: специальными знаками для обозначения неизвестных и их степеней, знаками для корня квадратного, для операций сложения и вычитания.
IX в. - среднеазиатский ученый Мухаммед ал-Хорезми подробно объясняет правила действия с числами, записанными в десятично-позиционной системе, и исследует квадратные уравнения. Слова «алгебра» и «алгоритм» впервые появились в переводе его трактатов. Первое из них означало операцию переноса членов из одной части уравнения в другую, а второе - искаженное имя автора (ал-Хорезми - Algorithmi); оно применялось первоначально только для обозначения правил вычисления по десятичной позиционной системе.
XI в. - математик и поэт Омар Хайям в трактате по алгебре систематически исследует не только уравнения первой и второй степеней, но и кубические. Решение их он строит геометрически при помощи пересечения параболы, гиперболы и окружности (см. стр. 474-476).
XII в. - индийский ученый Бхаскара-акарья сформулировал все правила действий с отрицательными числами и специально отметил, что корень квадратный из отрицательного числа не имеет действительных значений. Бхаскара отмечал также, что благодаря двузначности квадратного корня квадратное уравнение может иметь два решения.
XIII в. - Насирэддин Туси систематически излагает сферическую геометрию, исследует все случаи решения сферического треугольника, в том числе и по трем углам его, развивает дальнейшие идеи Хайяма о сближении отношений с числами и подробно излагает теорию составных частей.
XV в. - Гийяс ад-Дин Джемшид ал-Каши, работавший в обсерватории Улугбека близ Самарканда, вводит и систематически использует десятичные дроби. Этим десятичная позиционная система была распространена для записи любых действительных чисел. Он вычислил число p с точностью до 17 десятичных знаков. Ал-Каши сформулировал в общем виде правило возведения бинома в любую целую степень и описал способ извлечения корня любой степени.
XII - XIII вв. - на латинский язык переводятся арабские и греческие сочинения по математике. Постепенно распространяется десятичная позиционная система.
XIII в. - Леонардо Пизанский (Фибоначчи) излагает новую позиционную нумерацию, дает сведения по алгебре и арифметике, рассматривает различные числовые ряды.
XIV - XV вв. - совершенствуются алгебраические обозначения, вводятся обозначения для степени, для радикала и степеней неизвестного.
XVI в.- первый крупный успех европейской математики: итальянские ученые С. Ферро, Н. Тарталья и Дж. Кардано решили уравнения третьей степени в радикалах и ученик Кардано, Л. Феррари,- уравнение четвертой степени.
1572 г. - в «Алгебре» Р. Бомбелли впервые рассматривает мнимые числа a + b √‾- 1 и формулирует правила действия с ними. Сами эти числа он трактует как символы, удобные для получения результатов относительно действительных чисел,
1685 г. - С. Стевин вводит систему десятичных дробей.
XVI в. (вторая половина) - французский математик Ф. Виет вводит буквенные обозначения для неизвестных и постоянных величин и создает математическую формулу (см. стр. 476-478).
В XVII в. делает большие успехи механика земных и небесных тел, и в связи с этим возникают проблемы изучения зависимостей одних величин от других, проблемы определения скоростей, ускорений, площадей криволинейных фигур, центров тяжести и т. д. Для решения этих проблем в математике не было готового аналитического аппарата. Ученые начинают искать пути изучения переменных величин в математике, используя творения античных математиков. В результате в математику входит функциональная зависимость. С этих пор функция становится таким же основным объектом математики, как число и величина.
1614 г. - Д. Непер вводит логарифмы и публикует первые логарифмические таблицы. Несколько позднее таблицы логарифмов опубликовал Й. Бюрги.
1636-1637 гг. - Р. Декарт и П. Ферма вводят в математику метод координат, который позволяет сводить геометрические задачи к алгебраическим и изучать широкий класс функциональных зависимостей. Независимо друг от друга Декарт и Ферма начинают строить с помощью нового метода аналитическую геометрию (см. стр. 478-481).
1608-1650 гг. - развитие методов анализа бесконечно малых (методов определения объемов, площадей, центров тяжестей, касательных, экстремумов, скоростей, ускорений) в работах И. Кеплера, Б. Кавальери, Э. Торричелли, П. Ферма, Б. Паскаля, Дж. Валлиса и др.
503
30-40-е гг. XVII в. - П. Ферма закладывает основы теории чисел. Он формулирует знаменитые проблемы ее, которые в течение 200 лет были центральными в теоретико-числовых исследованиях.
70-80-е гг. XVII в. - И. Ньютон и Г. Лейбниц независимо друг от друга создают дифференциальное и интегральное исчисление (см. стр. 484, 487) и вводят в математический анализ основной его аппарат - бесконечные ряды. Ньютон распространил формулу возведения бинома в степень на случай, когда показатель степени - любое рациональное число.
1684 г. - выход в свет книги «Математические начала натуральной философии» И. Ньютона, в которой впервые было дано математическое построение основ классической механики земных и небесных тел.
1713 г. - Я. Бернулли формулирует и доказывает простейшую форму закона больших чисел - одного из основных законов теории вероятностей.
1748 г. - Л. Эйлер развивает учение о функциях как действительного, так и комплексного переменного. Эйлер подробно исследует элементарные функции хn, ах, log x :, sin x, cos x, находит для них выражения в виде бесконечных рядов и определяет логарифмы отрицательных и мнимых чисел (см. стр. 488-490).
1770-1771 гг. - Ж. Лагранж написал знаменитый мемуар «Размышления об алгебраическом решении уравнений», в котором проанализировал все методы решения в радикалах уравнений первых четырех степеней и показал, почему все эти методы не годятся для решения уравнений пятой степени. Он открыл, что разрешимость уравнений в радикалах зависит от свойств группы перестановок корней этого уравнения, и тем самым обратил внимание на значение изучения групп.
1796 г. - К. Гаусс показывает, что если и - простое число, то правильный n -угольник может быть построен с помощью циркуля и линейки, когда n имеет вид 22 k +i (см. стр. 490-492).
1799 г. - К. Вессель дал геометрическую интерпретацию комплексных чисел. Однако его работы остались неизвестными. В 1806 г. аналогичная геометрическая интерпретация была предложена Ж. Арганом. Всеобщее признание в математике интерпретация комплексных чисел получила только после того, как в 1832 г. К. Гаусс изложил основные ее идеи.
Математические методы проникают почти во все отделы физики, в химию, биологию, медицину, лингвистику, экономику. Сама математика необыкновенно расширяется количественно и претерпевает глубокие качественные изменения. В целом она поднимается на более высокую ступень абстракции.
1799-1825 гг. - К. Гаусс доказывает основную теорему алгебры, причем на протяжении указанного времени дает четыре различных доказательства ее.
1801 г. - К. Гаусс создает основы теории чисел. Он впервые развивает теорию сравнений, изучает до конца теорию квадратичных вычетов, доказывает основные теоремы этой теории, излагает теорию уравнений деления круга.
1821 г. - О. Коши развивает теорию пределов и на ее основе строит учение о функциях, определяет понятия суммы ряда, непрерывности функции, а позднее кладет учение о пределах в основу всего математического анализа. При изложении этой области науки мы до сих пор следуем пути, намеченному Коши, с теми усовершенствованиями, которые были внесены во второй половине XIX в. К. Вейерштрассом. Коши принадлежит также разработка основ теории функций комплексного переменного.
1824-1826 гг. - молодой норвежский математик Н. Абель доказал, что алгебраические уравнения степени n³ 5 неразрешимы в радикалах.
1827 г. - К. Гаусс развивает так называемую внутреннюю геометрию поверхностей, в которой каждая поверхность выступает как носительница своей особой геометрии.
1829-1830 гг. - Н. И. Лобачевский опубликовал свои первые работы по неевклидовой геометрии (см. стр. 492-494).
В 1832 г. - независимо от Н. И. Лобачевского систему неевклидовой геометрии построил Я. Бояи.
1830-1832 гг. - Э. Галуа находит признак того, решается ли данное уравнение с числовыми коэффициентами в радикалах. При этом он развивает методы теории групп и полей, которые приобрели огромное значение в математике и ее приложениях (см. стр. 494-496).
1832 г. - в связи со своими исследованиями по теории чисел К. Гаусс обобщает понятие целого числа на комплексные числа a+bi, где а и b - целые. Он определяет понятие простого числа, взаимно простых чисел, переносит на новые целые числа алгоритм нахождения наибольшего общего делителя и развивает всю арифметику целых комплексных чисел.
1840-1851 гг. - У. Гамильтон обобщает понятие комплексного числа, построив кватернионы - числа вида а+ bi + с j + dk, где i² = j² = k² =-1; а, b , с, d - действительные числа. Оказалось, что для этих чисел выполняются уже не все законы обычной арифметики. Так, умножение кватернионов не обладает свойством переместительности (ij ¹ ji).
1849 г. - П. Л. Чебышев получил первые после Евклида точные результаты о законе распределения простых чисел в натуральном ряде (см. стр. 496- 498).
1854 г. - Б. Риман вводит n -мерные пространства и, обобщая идеи Гаусса но внутренней геометрии поверхностей, дает способ построения всевозможных метрических неевклидовых геометрий. Римановы геометрии стали впоследствии основным математическим аппаратом общей теории относительности. Частным случаем римановых геометрий являются геометрия Евклида и геометрия Лобачевского.
1881-1882 гг. - Р. Дедекинд, Г. Кантор и К. Вейерштрасс строят тремя различными способами теорию действительных чисел. Вскоре в работах Дедекинда и особенно Кантора возникает новая важная область современной математики - теория множеств.
1899 г. - Д. Гильберт в «Основаниях геометрии» строит полную аксиоматику геометрии Евклида и анализирует соотношения между различными группами аксиом. С этого времени большое развитие в математике получает аксиоматический метод.
XX в. - созданы новые математические дисциплины, играющие чрезвычайно большую роль как в самой математике, так и в математическом естествознании и технике.
504
В древней Греции каждые четыре года проводились Олимпийские игры - общенациональные состязания в беге, метании диска, борьбе, езде на колесницах и т. п. Четырехгодичные промежутки между двумя Олимпийскими играми получили название олимпиад - по ним тогда вели счет времени. С конца прошлого века олимпиадами стали называть международные спортивные соревнования, которые также бывают раз в четыре года.
Математические олимпиады впервые возникли в нашей стране в 1934 г. Они хотя и называются олимпиадами, но совсем не связаны с четырехлетними перерывами и проводятся ежегодно. Вначале у нас были только городские олимпиады.
С 1960 г. организуются Всероссийские, а фактически Всесоюзные олимпиады. Их участники - школьники, соревнующиеся между собой в математических знаниях и сообразительности. Все соревнование состоит из четырех туров, на каждом из которых участникам предлагается решать задачи в письменном виде (обычно даются четыре задачи). Тот, кто хорошо решит задачи (быть может, не все), считается победителем в этом туре и допускается к следующему.
Вот некоторые задачи, которые предлагались на четвертом (заключительном) туре в 1963 и 1964 гг. (на III и IV Всероссийских олимпиадах).
VIII класс
1. Дан выпуклый четырехугольник ABCD. На продолжении стороны АВ откладывается отрезок ВМ=АВ, на продолжении стороны ВС - отрезок CN = ВС, на продолжении стороны CD - отрезок DP = CD и на продолжении стороны DA - отрезок 'AQ = AD.
Доказать, что площадь четырехугольника MNPQ в пять раз больше площади четырехугольника ABCD.
2. Доказать, что m ( m + 1) не является степенью целого числа ни при каком натуральном m .
3. Дан произвольный набор 2k + 1 целых чисел a1, a2, ..., a2с+1. Из него получается новый набор:
( a1 +a2 )/ 2; ( a2 + a3)/2; ...; ( a2k+1 + a1)/2.
Из этого набора - следующие по тому же правилу и т. д., причем все получающиеся числа - целые. Доказать, что все первоначальные числа равны.
4. Каждая из диагоналей выпуклого четырехугольника ABCD делит его площадь пополам. Доказать, что ABCD - параллелограмм.
IX класс
1. В клетки таблицы n X n ( n - нечетное) произвольным образом вписаны числа так, что в каждой клетке стоит число, равное +1 или -1. Произведение чисел, стоящих в каждой строке, обозначим через ak, а произведение чисел, стоящих в каждом столбце,- через bk (k= 1, 2,..., n). Доказать, что
a1 + a2 +...+аn +b1 + b2 + ...+ bn ¹ 0.
2. Решить в целых числах уравнение
где √‾n повторяется 1964 раза.
3. На плоскости нарисована сеть, образованная из правильных шестиугольников со стороной 1. Жук прополз, двигаясь по линиям сети, из узла А в узел В по кратчайшему пути, равному 100. Доказать, что половину всего пути он полз в одном направлении.
X-XI классы
1. Дан выпуклый шестиугольник ABCDEF. Известно, что каждая из диагоналей AD, BE, CF делит его площадь пополам. Доказать, что эти диагонали пересекаются в одной точке.
2. Дана арифметическая прогрессия, члены которой - целые положительные числа. Известно, что в этой прогрессии есть член, являющийся полным квадратом. Доказать, что прогрессия содержит бесконечно много таких членов.
3. На какое наименьшее число непересекающихся тетраэдров можно разбить куб?
В последние годы проводятся международные олимпиады, в которых принимают участие пока только социалистические страны. Так, летом 1962 г. в Чехословакии состоялась IV Международная математическая олимпиада учащихся двух последних классов средних школ. Участникам были предложены следующие задачи (в скобках после каждой задачи указано количество очков, начисляемое за ее решение).
1. Найти наименьшее натуральное число n , обладающее следующими свойствами:
а) его запись в десятичной системе заканчивается цифрой 6;
б) если зачеркнуть последнюю цифру 6 и перед оставшимися цифрами написать эту цифру 6, то полупится число в четыре раза больше исходного числа.
(6 очков)
2. Определить все действительные числа х, удовлетворяющие неравенству
√‾(3- x)- √‾( x +1)> 1/2 .
(6 очков)
3. Дан куб ABCDA'B'C'D' (ABCD и A'B'C'D'- соответственно верхнее и нижнее основания и АА' || ВВ' || СС' || DD'). Точка X движется с постоянной скоростью по сторонам квадрата ABCD в направлении ABCDA, и точка У движется с той же скоростью по сторонам квадрата В'С'СВ в направлении В'С'СВВ'. Точки X и У начинают двигаться в один и тот же момент из исходных положений А и В' соответственно.
Найти и начертить геометрическое место середин отрезков X У.
(8 очков)
4. Решить уравнение
cos² x +cos² 2 x +cos² 3 x =1.
(5 очков)
5. На окружности k заданы три различные точки А, В, С.
505
Построить (циркулем и линейкой) на окружности k четвертую точку D так, чтобы в полученный четырехугольник ABCD можно было вписать окружность.
(7 очков)
6. Дан равнобедренный треугольник А B С', r - радиус описанной окружности, r - радиус вписанной окружности. Докажите, что расстояние d между центрами окружностей есть
d= √‾(r(r-2 r)).
(6 очков)
7. Тетраэдр SABC обладает следующим свойством: существуют 5 сфер, касающихся ребер SA, SB, SC, АВ, ВС, СА или их продолжений.
Докажите, что а) тетраэдр SA ВС правильный, б) обратно - для каждого правильного тетраэдра существуют пять таких сфер.
(8 очков)
Для получения премии на олимпиаде требовалось 46-41 очко для I премии, 40-34 очка для II премии, 33-29 очков для III премии.
Всего было присуждено 4 первые, 12 вторых и 15 третьих премий. Из них советские школьники получили 2 первые, 2 вторые и 2 третьи.
Вот какие задачи пришлось решать участникам V Международной математической олимпиады, которая проходила летом 1963 г. в Польше.
1. Найти все вещественные корни уравнения
√‾( x² - р) +1 √‾( x² - 1) =х,
где р - вещественный параметр.
(6 очков)
2. Найти в пространстве геометрическое место вершин прямых углов, одна сторона которых проходит через данную точку А, а другая имеет по крайней мере одну общую точку с отрезком ВС.
(7 очков)
3. Доказать, что
cos( p /7)-cos(2 p /7)+cos(3 p /7) = 1/2 .
(6 очков)
4. Ученики А, В, С, D, E участвовали в одном конкурсе. Пытаясь угадать результаты соревнования, некто предполагал, что получится последовательность А, В, С, D, E. Но оказалось, что он не указал верно ни места какого-либо из участников, ни никакой пары следующих непосредственно друг за другом учеников. Некто другой, предполагая результат D, A, E, С, В, угадал правильно места двух учеников, а также две пары (непосредственно следующих друг за другом учеников). Каков был на самом деле результат конкурса?
(8 очков).
Дипломом I степени были награждены участники, набравшие от 35 до 40 очков, II степени - от 28 до 34 очков, III степени - от 21 до 27 очков. Советские школьники получили 4 диплома I степени (из 7), 3 диплома II степени (из 11), 1 диплом III степени (из 17). В журнале «Математика в школе», № 6, 1963, помещены решения задач III Всероссийской и V Международной олимпиад.
Со 2 по 10 июля 1964 г. в Москве в здании Московского университета проводилась VI Международная математическая олимпиада. Участникам были предложены следующие задачи:
1. а) Определить все целые положительные числа n , для которых число 2 n - 1 делится на 7.
б) Доказать, что ни при каком целом положительном n 2 n + 1 не делится на 7.
(7 очков)
2. Обозначим через а, b, с длины сторон некоторого треугольника. Доказать, что
a² ( b +с- а) + b² (а+ с- b)+ с² (а+ b- с) £ 3 а b с.
(7 очков)
3. В треугольнике А B С со сторонами а, b, с вписана окружность и построены ее касательные, параллельные сторонам данного треугольника. Эти касательные отсекают от данного треугольника ABC три новых треугольника. В каждый из таким образом построенных треугольников вписана окружность. Вычислить сумму площадей всех четырех кругов.
(6 очков)
4. Каждый из 17 ученых переписывается с остальными. В их переписке речь идет лишь о трех темах, каждая пара ученых переписывается друг с другом лишь в связи с одной темой. Доказать, что не менее трех ученых переписываются друг с другом об одной и той же теме.
(6 очков)
5. На плоскости даны пять точек. Среди прямых, соединяющих эти пять точек, нет параллельных, перпендикулярных и совпадающих. Проводим через каждую точку перпендикуляры ко всем прямым, которые можно построить, соединяя попарно остальные четыре точки. Каково максимальное число точек пересечения этих перпендикуляров между собой, не считая данные пять точек?
(7 очков)
6. Дан тетраэдр ABCD. Вершина D соединена с центром тяжести основания точкой D1. Через вершины треугольника А B С проведены прямые, параллельные DD1, до пересечения с плоскостями противоположных граней в точках A1 ,B1, С1. Доказать, что объем тетраэдра ABCD в три раза меньше объема тетраэдра A1 B1 C1 D1.
Будет ли верным результат, если точка D1 - произвольная точка внутри треугольника А B С?
(9 очков)
Для получения премии требовалось: 37-42 очка для I премии, 31-36 очков для II и 27-30 очков для III премии. Набравшим 30 очков были вручены дипломы участников олимпиады.
7 из 8 советских участников получили премии. Из них 3 первые (из 7), 1 вторую (из 9), 3 третьи (из 19) премии. Команда Венгрии получила 3 первые, 1 вторую и 1 третью премии; Польши -1 первую, 1 вторую и 3 третьих; Румынии - 2 вторые и 3 третьих; Чехословакии - 2 вторые и 2 третьи; ГДР - 1 вторую и 2 третьи; Болгарии - 3 третьи; Югославии - 1 вторую и 1 третью; Монголии - 1 третью премию.
Олимпиады повышают у учащихся интерес к математике. Возможно, что многие читатели Детской энциклопедии станут участниками олимпиад, некоторые же победителями на них, а впоследствии и учеными.
Предлагаемый читателю Детской энциклопедии список научно-популярных книг по математике разбит на несколько разделов, тематически связанных с группами математических статей настоящего тома. Исключение составляет лишь первый раздел, куда включены книги, относящиеся ко многим вопросам математики и ее истории. В каждом разделе (помимо обобщающих книг, с которых начинается раздел) указываются книги, дополняющие и углубляющие соответствующие статьи энциклопедии. Поэтому большинство книг рассчитано на школьников старших классов. В список включены также и книги, которые с интересом прочтут школьники VI - VIII классов (в аннотациях этих книг имеется соответствующее указание).
Общие вопросы
Колмогоров А. Н. О профессии математика. Изд.3. М., Изд-во Моск. ун-та, 1960. 30 стр.
Автор книги - выдающийся советский математик - рассказывает о работе математиков-исследователей, о так называемых математических способностях, об организации математического образования в нашей стране.
Люди русской науки. Очерки о выдающихся деятелях естествознания и техники. Кн. 1 [математика, механика, астрономия, физика, химия]. М., Физматгиз, 1961. 600 стр. с илл.
В очерках, написанных видными советскими учеными, рассказывается о жизни и творчестве выдающихся деятелей отечественного естествознания и техники. Двенадцать очерков посвящены математикам.
Каган В. Ф. Лобачевский и его геометрия. Общедоступные очерки. М., Гостехиздат, 1955. 304 стр. с черт.
Воронцова Л. А. Софья Ковалевская. М., «Молодая гвардия», 1959. 335 стр. с илл. (Жизнь замечательных людей).
Инфельд Л. Эварист Галуа - избранник богов. Перевод с англ. М., «Молодая гвардия», 1958. 368 стр. с илл. (Жизнь замечательных людей).
Оре О. Замечательный математик Нильс Хенрик Абель. Перевод с английского. М., Физматгиз, 1961. 344 стр. с илл.
Депман И. Я. Рассказы о решении задач. Л., Детгиз, 1957. 128 стр. с илл.
Десять рассказов, в которых наряду с решением задач есть интересные математические сведения. Автор на примерах показывает, как важно, решая задачи, внимательно относиться к каждому слову условия. Почти все задачи решаются при помощи четырех действий арифметики.
Эйдельс Л. М. Избушки на дорожках. М., Детгиз, 1960. 175 стр. с илл.
Повесть о школьной газете «Гипотенуза». Герои этой повести, члены математического кружка, сумели сделать по-настоящему интересными и занимательными простые математические задачи - такие же, какие ежедневно решаются в VI - VII классах.
Депман И. Я. Мир чисел [рассказы о математике]. Л., Детгиз, 1963. 72 стр. с илл. (Школьная б-ка).
В небольших очерках, доступных школьникам V-VIII классов, рассказывается о том, как люди на-
учились считать и мерить, о зарождении математики, успехах в ее развитии у разных народов, о возникновении основных понятий арифметики, алгебры, геометрии.
Нагибин Ф. Ф. Математическая шкатулка. Изд. 2. М., Учпедгиз, 1961. 167 стр. с илл.
Книга знакомит читателя с биографиями отечественных математиков, с интересным материалом по истории математики, математической логике, счетным приборам и машинам и с другими вопросами.
Перельман Я. И. Живая математика. (Математические рассказы и головоломки). Изд. 7. М., Физматгиз, 1962. 184 стр. с илл.
В увлекательной форме маленьких рассказов излагаются математические задачи и даются полезные практические приемы счета и измерения. Для чтения книги достаточно знания правил арифметики и элементарных сведений из геометрии.
Кордемский Б. А. Математическая смекалка. Изд. 7. М., Физматгиз, 1963. 568. стр. с илл.
Сборник из 365 математических миниатюр: разнообразных задач, математических игр, шуток и фокусов, требующих работы ума, развивающих смекалку и логичность в рассуждениях. В книге имеется материал для читателей с различной степенью подготовки.
Доморяд А. П. Математические игры и развлечения. М., Физматгиз, 1961. 268 стр. с илл.
Перельман Я. И. Занимательные задачи и опыты. М., Детгиз, 1959. 528 стр. с илл. (Школьная б-ка).
Радемахер Г., Теплиц О. Числа и фигуры. Опыты математического мышления. Перевод с немецкого. Изд. 3. М., Физматгиз, 1962. 264 стр. с илл. (Б-ка математического кружка).
Каждый из 27 маленьких очерков, посвященных различным вопросам математики,- образец доступного научного исследования. Ценность книги в том, что она не только знакомит с материалом, над которым работает наука, но и показывает научные методы в действии.
Литцман В. Где ошибка? Перевод с нем. М., Физматгиз, 1962. 192 стр. с илл.
Без сомнения, у всех вызовут улыбку утверждение: «2=1» и что «каждый треугольник- равнобедренный». Однако «доказательства» этих (и многих других столь же удивительных) утверждений можно найти в этой книге. Разумеется, эти «доказательства» содержат ошибки, но где? Ответ предоставляется найти читателю.
Дубнов Я.С. Ошибки в геометрических доказательствах. Изд. 3. М., Физматгиз, 1961. 68 стр. с черт. (Популярные лекции по математике).
Соминский И. С. Метод математической индукции. Изд. 6. М., Физматгиз, 1961. 48 стр. (Популярные лекции по математике).
Особый метод математических доказательств, позволяющий на основании частных наблюдений делать заключения об общих закономерностях.
Головина Л. И., Яглом И. М. Индукция в геометрии. Изд. 2. М., Физматгиз, 1961. 100 стр. с черт. (Популярные лекции по математике).
На подробно разобранных примерах указываются разнообразные применения метода математической индукции к решению геометрических задач.
Градштейн И. С. Прямая и обратная теоремы. (Элементы алгебры логики). Изд. 3.. М., Физматгиз, 1959. 128 стр. с илл.
507
Разъясняются логические отношения между прямой, обратной, противоположной и противоположной обратной теоремами. Излагаются элементы теории множеств и математической логики.
О фигурах и телах
Каган В. Ф. Очерки по геометрии. М., Изд-во Моск. ун-та, 1963. 571 стр. с илл.
Смогоржевский А. С. О геометрии Лобачевского. М., Гостехиздат, 1957. 68 стр. с илл. (Популярные лекции по математике).
Излагаются основные положения неевклидовой геометрии Лобачевского и краткие биографические сведения о нем.
Маркушевич А. И. Замечательные кривые. Изд. 2. М.-Л., Гостехиздат, 1952. 32 стр. с черт. (Популярные лекции по математике).
Автор рассказывает о свойствах некоторых кривых линий. Книга рассчитана на учащихся VII - VIII классов.
Перельман Я. И. Занимательная геометрия. Изд. 11. М., Физматгиз, 1959. 302 стр. с черт.
О многих интересных геометрических задачах, возникающих в лесу, в поле, у реки, на дороге, говорится в этой книге.
Островский А. И., Кордемский Б. А. Геометрия помогает арифметике. М., Физматгиз, 1960. 168 стр. с илл.
Наглядные (геометрические) решения задач всегда считаются «красивыми». Множество интересных задач и их наглядных решений приводится в этой красочно изданной книге.
Зетель С. И. Геометрия линейки и геометрия циркуля. Изд. 2. М., Учпедгиз, 1957. 163 стр. с черт.
Всем школьникам известно, как увлекательны задачи на построение с помощью циркуля и линейки. А можно ли решать такие задачи (и какие именно) с помощью только одного циркуля или одной линейки? В книге дается ответ на этот вопрос.
Гельфанд И. М., Глаголева Е. Г., Кириллов А. А. Метод координат. М., «Наука», 1964. 72 стр. с черт. (Б-ка физико-математической школы).
Один из важнейших методов решения многих геометрических и других задач алгебраическим путем и применение этого метода к исследованию фигур в четырехмерном пространстве.
Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы элементарной математики, Ч. 2-3. М., Гостехиздат, 1952-1954. (Б-ка математического кружка).
Ч. 2.- Геометрия (планиметрия). 380 стр. с черт. (150 задач).
Ч. 3.- Геометрия (стереометрия). 267 стр. с черт. (119 задач).
Сборники нешаблонных геометрических задач, снабженных решениями. Среди задач по планиметрии имеются доступные школьникам VII - VIII классов.
О числах и уравнениях
Александров П. С. Введение в теорию групп. Изд. 2. М., Учпедгиз, 1951. 126 стр. с черт.
Берман Г. Н. Число и наука о нем. Общедоступные очерки по арифметике натуральных чисел. Изд. 3. М., Физматгиз, 1960. 164 стр. с илл.
Рассматриваются свойства натуральных чисел, различные способы их записи и обозначения, вопросы делимости чисел друг на друга.
Перельман Я. И. Занимательная арифметика. Загадки и диковинки в мире чисел. Изд. 9. М., Физматгиз, 1959. 184 стр. с илл.
Разнообразные арифметические задачи изложены в виде увлекательных рассказов. Для решения их достаточно знакомства с правилами арифметики.
Перельман Я. И. Занимательная алгебра. Изд. 10. М., Физматгиз, 1959. 184 стр. с илл.
Многие вопросы школьного курса алгебры излагаются в виде задач с необычайными сюжетами, сопровождаются занимательными экскурсиями в область истории математики, неожиданными применениями.
Маркушевич А. И. Комплексные числа и конформные отображения. Изд. 2. М., Физматгиз, 1960. 56 стр. с черт.
Комплексные числа вводятся геометрически, как векторы на плоскости. В книге рассказывается о применениях их к геометрическим преобразованиям, сохраняющим величины углов (конформным отображениям).
Гельфонд А. О. Решение уравнений в целых числах. Изд. 2. М., Гостехиздат, 1957. 64 стр. с илл. (Популярные лекции по математике).
Каждый, кто знаком с решением уравнений, знает, что одно уравнение первой степени с двумя неизвестными имеет бесчисленно много решений. Нетрудно найти и те решения, которые выражаются целыми числами. А как решить ту же задачу, если дано уравнение второй или более высокой степени с несколькими неизвестными? О некоторых результатах в ее решении рассказывается в этой книге.
Курош А. Г. Алгебраические уравнения произвольных степеней. М.-Л., Гостехиздат, 1951. 32 стр. с илл. (Популярные лекции по математике).
Вопрос о том, какие из уравнений степени более второй могут быть решены (и как), разбирается в этой книге.
Виленкин Н. Я. Метод последовательных приближений. М., Физматгиз, 1961. 64 стр. с илл. (Популярные лекции по математике).
Метод приближенного решения уравнений, как алгебраических, так и трансцендентных (тригонометрических, показательных и др.).
Шклярский Д. О., Ченцов Н. Н., Яглом И. М. Избранные задачи и теоремы элементарной математики. Ч. 1. Арифметика и алгебра. Изд. 3. М., Физматгиз, 1959. 455 стр. с илл. (Б-ка математического кружка).
Сборник 320 нешаблонных задач, снабженных решениями. Среди задач имеются доступные школьникам VII - VIII классов (эти задачи отмечены особо).
Об основных понятиях высшей математики
Зельдович Я. Б. Высшая математика для начинающих и ее приложения к физике. Изд. 2. М., Физматгиз, 1963. 560 стр. с илл.
В простой и наглядной форме объясняются основные понятия дифференциального и интегрального исчисления - важнейшего раздела высшей математики. На их основе рассмотрено большое число физических вопросов.
508
Натансон И. П. Простейшие задачи на максимум и минимум. Изд. 3. М.- Л., Физматгиз, 1960. 32 стр. с черт. (Популярные лекции по математике).
Несколько способов (с применением только алгебраических средств) решения задач на определение максимума или минимума исследуемых величин.
Шилов Г. Е. Как строить графики. М., Физматгиз, 1959. 24 стр. с илл. (Популярные лекции по математике).
Приемы построения графиков функций на примерах прямой и обратной пропорциональной зависимостей и многочленов второй степени.
Болтянский В. Г. Что такое дифференцирование? Изд. 2. М., Физматгиз, 1960. 64 стр. с илл. (Популярные лекции по математике).
На примерах, взятых из физики, поясняются некоторые понятия высшей математики (производная, дифференциальное уравнение, натуральный логарифм, число е).
Натансон И. П. Суммирование бесконечно малых величин. Изд. 3. М., Физматгиз, 1960. 56 стр. с черт. (Популярные лекции по математике).
Весьма разнообразные задачи физики (например, определение давления жидкости на стенки сосуда, вычисление работы) и геометрии (например, определение площади криволинейных фигур, объема тел) приводят к необходимости вычисления сумм одного типа - сумм безгранично возрастающего числа безгранично убывающих слагаемых. Понятие предела таких сумм лежит в основе интегрального исчисления - раздела высшей математики, о нем и идет речь в этой книге.
Маркушевич А. И. Площади и логарифмы. М.- Л., Гостехиздат, 1952. 51 стр. с черт.
Логарифмы определяются, как площади некоторых криволинейных фигур, связанных с графиком обратной пропорциональности (гиперболой), и отсюда выводятся все их свойства. Книга является своеобразным введением в интегральное исчисление.
Маркушевич А. И. Ряды. Элементарный очерк. Изд. 3. М., Физматгиз, 1961. 188 стр. с илл.
Можно ли найти значения синуса какого-либо угла или логарифма чисел, не прибегая к таблицам? Да, но для этого надо знать представление этих функций в виде бесконечных рядов. О понятии бесконечного ряда, основных свойствах рядов, о рядах для элементарных функций рассказывается в этой книге.
Некоторые вопросы современной математики и кибернетики
Гнеденко Б. В., Хинчин А. Я. Элементарное введение в теорию вероятностей. Изд. 6. М., Физматгиз, 1964. 144 стр. с илл.
Проблемы физики и биологии, автоматического управления и лингвистики и многие другие приводят к необходимости решать многочисленные задачи, связанные с выяснением возможного хода процессов, на которые влияют случайные факторы. Поэтому теория вероятностей - математическая наука, изучающая закономерности случайных явлений,- стала одним из основных математических методов современного естествознания и техники. В этой книге дается элементарное изложение основных понятий теории вероятностей.
Яглом А. М., Яглом И. М. Вероятность и информация. Изд. 2. М., Физматгиз, 1960. 316 стр. с черт.
Книга является введением в новую область математики - теорию информации, тесно связанную с кибернетикой и имеющую ряд приложений в технике связи, биологии, лингвистике и т. д.
Вентцель Е. С. Элементы теории игр. Изд. 2. М., Физматгиз, 1961. 68 стр. с черт. (Популярные лекции по математике).
Основные положения теории игр - важного раздела современной математики - иллюстрируются подробно разобранными примерами.
Берг А. И. Кибернетика и надежность. М., «Знание», 1963. 32 стр.
Автор книги - выдающийся советский ученый - рассказывает о возможностях кибернетики, о научных, технических и организационных мерах повышения надежности кибернетической техники, о том, как служит и будет служить кибернетика делу коммунизма.
Кобринский Н. Е., Пекелис В. Д. Быстрее мысли. М., «Молодая гвардия», 1959. 389 стр. с илл.
Авторы живо и интересно рассказывают о многих проблемах, имеющих прямое отношение к кибернетике. Книга богато иллюстрирована остроумными рисунками.
Кондратов А. М. Число и мысль. М., Детгиз, 1963. 142 стр. с илл.
Увлекательные рассказы о достижениях и возможностях кибернетики.
Полетаев И. А. Сигнал. О некоторых понятиях кибернетики. М., «Советское радио», 1958. 404 стр. с илл.
В книге дано всестороннее освещение основ кибернетики. Разделы, требующие специальных знаний по математике, выделены и могут быть опущены без большого ущерба для понимания остального материала.
Теплов Л. П. Очерки о кибернетике. Изд. 2. М., «Московский рабочий», 1963. 416 стр. с илл.
Кобринский А. Е. Числа управляют станками. М., Изд-во АН СССР, 1961. 192 стр. с илл. (Научно-популярная серия).
Не прибегая к формулам, автор рассказывает о том, как действует автомат с цифровым управлением, как он устроен, какие трудности возникали при его создании. Книга знакомит также с системами счисления, методами кодирования, принципом обратной связи.
Сапарина Е. В. Кибернетика внутри нас. М., «Молодая гвардия», 1962. 304 стр. с илл.
Занимательные рассказы о сложных проблемах применения идей и методов кибернетики в области медицины, физиологии, психологии и лингвистики.
Кондратов А. М. Математика и поэзия. М., «Знание», 1962. 48 стр с илл.
Математические методы - мощное орудие исследования в самых различных областях знаний. В этой книге рассказывается об их применении в изучении стиха, об анализе творчества с позиций кибернетики.
Зарипов Р. X. Кибернетика и музыка. М, «Знание», 1963. 56 стр. с илл.
О попытках изучения музыкального творчества методами кибернетики рассказывается в этой книге. Излагаются опыты автора по сочинению музыки на электронной вычислительной машине «Урал». Описание методов композиции сопровождается нотными примерами мелодий («Уральскими напевами»), сочиненными машиной «Урал».
Архангельский Н. А., Зайцев Б. И. Автоматические цифровые машины. М., Физматгиз, 1958. 127 стр. с илл. (Популярные лекции по математике).
Смирнов А. Д. Современные математические машины. М., Физматгиз, 1959, 112 стр. с илл.
Тукачинский М. С. Машины-математики. М., Физматгиз, 1958. 130 стр. с илл.
509
Абак - счетная доска у древних греков и римлян (а затем и в Западной Европе вплоть до XVIII в.), применявшаяся для арифметических вычислений. Принцип устройства подобен нашим счетам.- 269
Абель, Нильс Генрик (1802-1829) - норвежский математик. Доказал (1824) неразрешимость в радикалах уравнения 5-й и более высоких степеней в общем случае. Другие его работы относятся ко многим вопросам математического анализа.- 327, 417, 496, 504
Абсолютная величина. - 330
Абсолютная геометрия. - 297
Абсцисса - одна из декартовых координат точки.- 330
Автомат - понятие кибернетики.- 443
Адамс, Джон Кауч (1819-1892) - английский астроном.- 372
Адрес - величина, определяющая местоположение информации в электронной вычислительной машине.- 434
Аксиома - положение, принимаемое без доказательства в пределах данной математической дисциплины.- 295, 296, 313, 411
Аксиома о параллельных. - 315, 316
Аксиоматика - система аксиом данной математической дисциплины. Об аксиоматике геометрии см. стр. 313, 504; об аксиоматике алгебры см. стр. 411
Аксиоматический метод.- 299, 504
Алгебра - часть математики, развившаяся в связи с задачей о решении уравнений. В дальнейшем развитии предмет алгебры значительно расширился (см. стр. 408-426, 477). О происхождении термина «алгебра» см. стр. 325, 475, 503
Алгебра множеств. - 384-386
Алгебраическая символика.- 477, 480, 502, 503
Алгебраическое уравнение - уравнение, которое можно (после преобразований) привести к виду приравненного нулю многочлена относительно неизвестных, (см. стр. 324, 415 - 417, 480, 496, 504). Решение уравнений 1-й и 2-й степеней было известно еще в древности (стр. 323-327). В XVI в. было найдено решение уравнений 3-й и 4-й степеней (стр. 327, 503). В XIX в. было доказано, что корни уравнений степени выше 4-й в общем виде нельзя выразить через коэффициенты (стр. 417, 504).
Алгебры основная теорема. -327, 328, 416, 491, 504
Алгол - условное название универсального языка программирования для быстродействующих электронных вычислительных машин.- 438
Алгоритм (или алгорифм) - совокупность математических операций, выполняемых в определенном порядке для решения задач данного типа (стр. 432, 443). О происхождении термина «алгоритм» см. стр. 503.
Алфавит абстрактный - понятие кибернетики.- 442
Алфавитная нумерация - способ записи чисел, в котором в качестве цифровых знаков употребляются буквы алфавита.- 273-275
Ампер, Андре Мари (1775-1836) - французский ученый. Основные работы относятся к различным вопросам физики.- 441
Аналитическая геометрия - раздел математики, в котором свойства геометрических фигур (точек, линий, поверхностей и их совокупностей) изучаются средствами алгебры при помощи метода координат.- 263, 329, 479, 481, 502, 503
Аполлоний Пергский - древнегреческий математик, работавший ок. 200 до н. э. в Александрии. Важнейшее его сочинение - «Конические сечения», где рассматриваются свойства эллипса, гиперболы и параболы; оказал большое влияние на развитие математики нового времени.- 263, 478, 502
Арабские цифры - традиционное название десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,- с помощью которых по десятичной системе счисления записываются любые числа. О происхождении термина см. стр. 277
Арган, Жан Робер (1768-1822) - французский математик. Автор работы (1806), содержащей геометрическую интерпретацию комплексных чисел.- 504
Аргумент - независимая переменная величина.- 342
Ариабхата (p. в V в.- дата смерти неизв.) - индийский астроном и математик. В его сочинениях встречаются извлечение квадратного и кубического корней из чисел, простейшие задачи на составление и решение уравнений, среди которых имеется неопределенное уравнение с двумя неизвестными и его решение в целых числах.- 503
Арифметическая прогрессия - последовательность чисел, из которых каждое следующее получается из предыдущего прибавлением постоянного числа.- 451, 501
Арифметическое среднее. - 451
Арифметическое устройство - одно из пяти основных устройств быстродействующей электронной вычислительной машины.- 433
Архимед (ок.287-212 до н. э.) - древнегреческий математик и механик.- 262, 273, 293, 327, 452, 472-474, 475, 502
Архимеда аксиома.- 502
Архимеда спираль. - 339
Ассоциативность, ассоциативный (сочетательный) закон - свойство сложения и умножения, выражаемое формулами: (а+ b)+с=а+( b +с), а( b с)=(а b)с.- 383, 385, 386, 390, 400, 410
Аффинное преобразование - геометрическое преобразование, при котором прямые переходят в прямые.- 421
Ахмеса папирус - один из двух дошедших до нашего времени математических папирусов древнего Египта; составлен египетским писцом Ахмесом ок. 2000 до н. э. Представляет собой собрание 84 задач, имеющих прикладной характер.- 322
¹ Имена ученых, математические понятия и термины, вошедшие в словарь-указатель, сопровождаются развернутым объяснением лишь в том случае, если они недостаточно подробно описаны в статьях энциклопедии.
510
Барроу, Исаак (1630-1677) - английский математик, владевший в геометрической форме основными идеями дифференциального и интегрального исчислений. Учитель И. Ньютона.- 368, 483
Бартелье, Мартин - немецкий математик конца XVIII - начала XIX в. Руководил ранним образованием К. Гаусса. С 1808 г. работал в Казанском университете, где преподавал математику. У него учился Н. И. Лобачевский.- 490, 492
Бернулли - семья швейцарских ученых, давшая 11 видных математиков. Наиболее известны: братья Якоб Бернулли (1654-1705) (стр. 456, 459, 504) и Иоганн Бернулли (1667-1748) (стр. 488), сотрудничавшие с Г. Лейбницем в разработке основ дифференциального и интегрального исчислений; дети Иоганна Бернулли - Николай (1695-1726) (стр. 488) и Даниил (1700- 1782) (стр. 488), работавшие в Петербургской Академии наук.
Бесконечный ряд - выражение a1 + a2 +...+ an +..., члены которого а1, а2, ..., аn ,... - числа (числовой ряд) или функции (функциональный ряд). В исследовании и вычислении функций большое значение имеет представление их в виде рядов, членами которых являются более простые функции.- 484, 503, 504
Библиотека стандартных подпрограмм. - 438
Бином - двучлен. Бином Ньютона - формула, выражающая целую положительную степень суммы двух слагаемых через степени этих слагаемых.- 476, 503, 504
Бионика - раздел кибернетики.- 450
Больцано, Бернард (1781-1848) - чешский математик. Основная часть его рукописного научного наследия исследована лишь в XX в. Главный математический труд «Учение о функциях», написанный в 1830 г., увидел свет лишь через 100 лет; в нем Больцано ввел ряд понятий и теорем математического анализа, обычно связываемых с именами других ученых.- 375
Больших чисел закон - одно из основных положений теории вероятностей.- 459, 504
«Большое число». - 275
Бомбелли, Рафаэль - итальянский математик и инженер 2-й половины XVI в. В его сочинении «Алгебра» (1572) дано первое изложение простейших действий над мнимыми числами.- 327, 503
Бояи, Янош (1802-1860) - венгерский математик. Независимо от Н. И. Лобачевского и несколько позже его изложил- (1832) основные положения неевклидовой геометрии.- 297, 298, 504
Брахмагупта (598-660 ?) - индийский математик и астроном.- 503
Булева алгебра - понятие математической логики.- 389
Буль, Джордж (1815-1864) - английский математик и логик, основоположник математической логики.- 389, 394
Бхаскара (Бхаскара-акария) (р. 1114 - год смерти неизв.) - индийский математик и астроном. Дал изложение методов решения ряда задач алгебры и теории чисел, в частности решения в целых числах неопределенного уравнения 2-й степени. - 326, 503
Бюрги, Йобст (1552-1632) - швейцарский ученый. Независимо от Дж. Непера составил (1620) логарифмические таблицы.- 503
Вавилонская шестидесятеричная нумерация. - 275, 276, 501
Валлис, Джон (1616-1703) - английский математик. Основной труд «Арифметика бесконечного» (1655) сыграл важную роль в создании интегрального исчисления. Им введен общепринятый ныне знак ¥ для бесконечности.- 503
Варинг, Эдуарт (1736-1798) - шотландский математик. Основные работы относятся к. алгебре и теории чисел; особенно известна постановка так называемой задачи Варинга.- 286
Вводное устройство - одно из пяти основных устройств быстродействующей электронной вычислительной машины.- 433
Вейерштрасс, Карл Теодор Вильгельм (1815- 1897) - немецкий математик. Его труды посвящены многим областям математики. Большое значение имеет разработанная им система логического обоснования математического анализа, покоящаяся на построенной им теории действительных чисел.- 498, 504
Вектор - направленный отрезок, при помощи которого изображаются векторные величины - сила, скорость, ускорение и др. Название «вектор» происходит от латинского vector - несущий, ведущий.- 397
Векторная алгебра. - 402
Венна диаграмма. - 385
Вероятностей теория - важный в приложениях раздел математики, изучающий закономерности массовых явлений, носящих случайный характер.- 452, 455, 497, 504
Вероятность. - 456
Вессель, Каспер (1745-1818) - датский математик. Автор работы (1799), посвященной векторному исчислению и содержащей первое полное геометрическое построение теории комплексных чисел.- 504
Взаимно однозначное соответствие. - 376
Виет, Франсуа (1540-1630) - французский математик.- 325, 327, 476-478, 503
Виета теорема - теорема, устанавливающая зависимость между корнями и коэффициентами алгебраического уравнения.- 478
Винер, Норберт (1894-1964) - американский ученый. Основоположник новой науки - кибернетики. Ранние его работы относятся ко многим важным областям современной математики.- 442
Виноградов, Иван Матвеевич (р. 1891) - советский математик, академик (с 1929 г.), Герой Социалистического Труда (1945). Научная деятельность относится к области теории чисел, в которую он ввел новые методы, оказавшие решающее влияние на ее развитие и позволившие ему решить ряд труднейших проблем.- 286
Внутренняя геометрия. - 504
Ворон - наименование в славянской нумерации числа 1048 .- 275
Вороной, Георгий Феодосьевич (1868-1908) русский математик, член-корреспондент Петербургской Академии наук (с 1907 г.). Его исследования относятся ко многим вопросам теории чисел.- 498
Вращение - геометрическое преобразование.- 301
Вывод - понятие математической логики.- 396
Выводное устройство - одно из пяти основных устройств быстродействующей электронной вычислительной машины.- 434
Высказывание - понятие математической логики.- 392
Высшая математика. - 263
511
Галилей, Галилео (1564-1642) - итальянский ученый.- 502
Галуа, Эварист (1811-1832) - французский математик.- 327, 425, 494-496, 504
Галуа теория. - 425
Гамильтон, Уильям Роуан (1805-1865) - английский математик. Построил своеобразную систему чисел - так называемые кватернионы,- явившуюся одним из источников векторного исчисления.- 409, 504
Гармонический ряд. - 451
Гармоническое среднее. - 451
Гарриот, Томас (1560-1621) - английский математик. Большую роль сыграл в развитии алгебраических обозначений, его запись уравнений весьма близка к современной. Ввел знаки > и < (опубликовано посмертно в 1631 г.).- 325
Гаусс, Карл Фридрих (1777-1855) - немецкий математик.- 297, 298, 327, 328, 416, 418, 458, 490-492, 496, 504
Гельфонд, Александр Осипович (р. 1906) - советский математик, член-корреспондент Академии наук СССР (с 1939 г.). Специалист в области теории чисел и теории функций. Открыл новые методы доказательства трансцендентности чисел.- 286
Геометрическая алгебра. - 501
Геометрическая прогрессия - последовательность чисел, из которых каждое следующее получается из предыдущего умножением на постоянное число.- 451, 502
Геометрическое преобразование. - 301, 419
Геометрическое среднее. - 451
Геометрия - часть математики, которая изучает пространственные отношения и формы тел (см. стр. 262, 293-295, 299, 309, 313, 422, 424, 501). О происхождении названия см. стр. 293
Герон - древнегреческий ученый, работавший в Александрии, вероятно, в I в. Его математические работы являются энциклопедией античной прикладной математики. В лучшей из них («Метрике») даны правила и формулы для точного и приближенного расчета различных геометрических фигур.- 326
Гиббс, Джозайя Уиллард (1839-1903)- американский физик.- 352
Гильберт, Давид (1862-1943) - немецкий математик. Его исследования оказали большое влияние на развитие математики XX в.- 286, 299, 494, 504
Гипербола - плоская кривая, состоящая из двух бесконечных ветвей; является геометрическим местом точек, разность расстояний которых от двух данных равна постоянной величине.- 308, 333, 336, 502
Гиппократ Хиосский - древнегреческий геометр 2-й половины V в. до н. э. Автор первого систематического сочинения по геометрии (не дошедшего до нас), которое, вероятно, охватывало материал первых четырех книг евклидовых «Начал».- 296, 327, 502
Гомотетия - геометрическое преобразование, частный случай подобия.- 303
Гросс - дюжина дюжин, т. е. 12² =144 однородных предметов.- 267
Группа - понятие современной алгебры.- 421-423, 426 496, 504
Гюйгенс, Христиан (1629-1695) - нидерландский ученый. Основные труды относятся к физике и астрономии, математические работы - к теории вероятностей.- 456
Движение - геометрическое преобразование, меняющее положение фигуры, но сохраняющее ее форму и размеры.- 300, 309, 420, 422
Двоичная система счисления - система счисления, в которой за основание принимается число «два», так что все числа записываются с помощью только двух цифр: 0 и 1.- 266, 267, 428-430
Двойного отрицания закон - один из законов математической логики.- 395
Двух ложных положений метод - метод решения уравнений.- 323, 324
Дедекинд, Юлиус Вильгельм Рихард (1831-1916) - немецкий математик. Работал в области теории чисел и алгебры. Развил учение о непрерывности числового ряда, имеющее большое значение для строгого обоснования математического анализа.- 502, 504
Дедуктивная система. - 296, 502
Дезарг, Жирар (ок. 1593 - ок. 1662) - французский математик. Систематическое применение перспективного изображения в его исследованиях оказало большое влияние на создание в XIX в. новой геометрической дисциплины - проективной геометрии.- 502
Декарт, Рене (1596-1650) - французский ученый.- 263, 324, 325, 327, 329, 476, 478-480, 481, 502, 503
Декартовы координаты.- 330
Делоне, Борис Николаевич (р. 1890) - советский математик, член-корреспондент Академии наук СССР (с 1929 г.). Работы относятся к алгебре, геометрии, теории чисел и кристаллографии.- 285
Десятичная дробь. - 503
Десятичная система счисления - система счисления, в которой за основание принимается число «десять», так что все числа записываются с помощью десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.- 266, 276, 277, 503
Дизъюнкция - понятие математической логики.- 392, 393
Диофант - древнегреческий математик, работавший в Александрии, вероятно, в III в. Его трактат «Арифметика» (от которого сохранились только 6 книг из 13) сыграл большую роль в развитии алгебры и теории чисел.- 280, 325, 326, 502
Диофантово уравнение - см. неопределенное уравнение.
Дистрибутивность, дистрибутивный (распределительный) закон - свойство сложения и умножения, выражаемое формулой: (a+b+...+ с) m = am+bm+ ...+ cm . - 383, 386, 390, 410
Дифференциальное исчисление - математическая дисциплина; вместе с интегральным исчислением составляет важную часть математики - математический анализ.- 263, 474, 484, 486, 502, 504
Дифференциальное уравнение - уравнение, связывающее искомую функцию и ее производные.- 370
Дифференцирование - операция нахождения производных.- 365
Додекаэдр - один из пяти типов правильных многогранников; имеет 12 граней (пятиугольных), 30 ребер, 20 вершин (в каждой вершине сходится 3 ребра).- 296, 501, 502
Доказательство от противного - метод доказательства теорем.- 396
«Дополнение множества. - 390
Дюжина - двенадцать однородных предметов.-
512
Евдокс Книдский - древнегреческий математик и астроном IV в. до н. э. Разработал общую теорию пропорций и некоторые приемы доказательств геометрических теорем. Его сочинения до нас не дошли.- 502
Евклид - древнегреческий математик, работавший в Александрии в III в. до н. э. Автор «Начал» - первого дошедшего до нас теоретического трактата по математике.- 262, 296-299, 313, 316, 326, 492, 502, 504
Евклида алгоритм. - 502
Евклидова геометрия. -313-318, 320, 321, 504
Египетская нумерация. - 272
Жирар, Альберт (1595-1632) - голландский математик. Впервые (1629) высказал основную теорему алгебры, доказанную лишь в 1799 г. К. Гауссом. При решении уравнений, наряду с положительными корнями, рассматривал и отрицательные. Ввел (1629) употребляемый ныне знак корня.- 327
Запоминающее устройство - одно из пяти основных устройств быстродействующей электронной вычислительной машины.- 433, 443
Золотарев, Егор Иванович (1847-1878) - русский математик. Работал в области теории чисел и математического анализа.- 498
Игр теория - математическая дисциплина.- 466-471
Игра - понятие теории игр.- 466
Икосаэдр - один из пяти типов правильных многогранников; имеет 20 граней (треугольных), 30 ребер, 12 вершин (в каждой вершине сходится 5 ребер).- 296, 502
Интеграл - одно из основных понятий математического анализа. Знак интеграла ∫ - видоизмененное латинское S (от слова Summa) - введен Г. Лейбницем (1675).- 356, 358, 359
Интегральное исчисление - математическая дисциплина; вместе с дифференциальным исчислением составляет важную часть математики - математический анализ.- 263, 473, 484, 486, 502, 504
Информация - понятие кибернетики.- 442
Ионийская нумерация - алфавитная нумерация, употреблявшаяся в древней Греции.- 273
Иррациональные числа - числа, не являющиеся рациональными, т. е. не могущие быть точно выраженными дробью m/n, где m и n - целые числа.- 480
Исключенного третьего закон - один из законов математической логики.- 394
Исчерпывания метод - метод доказательства, применявшийся математиками древности при определении площадей и объемов.- 502
Кавальери, Бонавентура (1598-1647) - итальянский математик. В труде «Геометрия» (1635) развил новый метод определения площадей и объемов (так называемый метод неделимых), оказавший большое влияние в формировании интегрального исчисления. Ввел (1632) употребляемый ныне знак (log) логарифма.- 503
Кантор, Георг (1845-1918) - немецкий математик. Основоположник теории множеств, оказавшей большое влияние на развитие современной математики.- 379, 383, 504
Канторович, Леонид Витальевич (р. 1912) - советский математик, академик (с 1964 г.). Автор работ по многим вопросам математики и математической экономики.- 444
Кардано, Джеронимо (1501-1576) - итальянский математик. Его работы сыграли важную роль в развитии алгебры: он одним из первых в Европе стал допускать отрицательные корни уравнений, у него впервые встречаются мнимые величины, его имя носит формула решения кубического уравнения.- 327, 503
Касательная. -363, 473, 481, 502, 503
ал-Каши, Джемшид ибн-Масуд (г. рожд. неизв.- ум. ок. 1436) - математик и астроном XV в., работавший ок. 1420-1430 гг. на Самаркандской обсерватории. Впервые ввел в употребление десятичные дроби и описал правила действия над ними, изложил приемы извлечения корней любой степени, указал способ приближенного решения уравнений 3-й степени.- 328, 503
Квадрант - плоский сектор с центральным углом в 90°, 1/4 часть круга. Квадрант плоскости - любая из четырех областей (углов), на которые плоскость делится двумя взаимно перпендикулярными прямыми.- 330
Квадратичная иррациональность. - 417, 502
Квадратное уравнение - алгебраическое уравнение 2-й степени.- 326, 501-503
Квадратриса - плоская кривая, с помощью которой древнегреческий ученый Динострат (IV в. до. н. э.) выполнил квадратуру круга.- 502
Квадратура круга - знаменитая задача древности: с помощью циркуля и линейки построить квадрат, равновеликий данному кругу. Эта задача сводится к построению числа я, поэтому, как установлено в XIX в., указанными средствами она неразрешима. Если же привлечь к построению дополнительные средства, например квадратрису, то задача становится разрешимой.- 418, 502
Кватернионы - система чисел, более общая, чем комплексные числа.- 409, 412, 419, 504
Кельвин (Томсон, Уильям) (1824-1907) - английский физик.- 352
Кеплер, Иоганн (1571 -1630) - австрийский ученый. Основные работы относятся к астрономии. В математическом сочинении «Новая стереометрия винных бочек» для решения геометрических задач предложил способ, содержащий начатки интегрального исчисления.- 354, 368, 402, 502, 503
Кибернетика - научное направление, основы которого заложены в 40-х гг. XX в. в работах Н. Винера.- 441-451
Клейн, Феликс (1849-1925) - немецкий математик. Автор многих работ по геометрии, алгебре и теории функций.- 309, 422, 424
513
Клинописные математические тексты - математические тексты древней Вавилонии и Ассирии; охватывают период от 2 тысячелетия до н. э. и до начала нашей эры; написаны клинописью на глиняных пластинках. В них впервые встречаются позиционная система счисления и квадратные уравнения.- 262, 275, 276, 501
Ковалевская, Софья Васильевна (1850-1891) - русский математик.- 498, 499
Код - система «команд», применяемых в быстродействующих электронных вычислительных машинах.- 434
Кодирование. - 442
Коллинеарные векторы. - 398
Колмогоров, Андрей Николаевич (р. 1903) - советский математик, академик (с 1939 г.), Герой Социалистического Труда (1963). Научные работы относятся ко многим областям современной математики и теоретическим вопросам кибернетики.- 461
Колода - наименование в славянской нумерации числа 1049 .- 275
Кольцо - понятие современной алгебры.- 412
Команда. - 434
Коммутативность, коммутативный (переместительный) закон - неизменяемость суммы (или произведения) при перестановке слагаемых (или множителей): a+b=b+a, ab=ba. - 383, 385, 386, 389, 400, 410
Комплексные числа - числа вида а+ bi , где а и b - действительные числа, а i - так называемая мнимая единица - число, квадрат которого равен -1.- 504
Конечная игра. - 467
Конические сечения - эллипс, гипербола, парабола - линии пересечения круглого (с двумя полостями) конуса с плоскостями, не проходящими через его вершину.- 308, 502
Континуум-гипотеза. - 383
Конус. -288, 502
Конъюнкция - понятие математической логики.- 392, 393
Координатные линии. - 339
Координаты точки - числа, определяющие ее положение на прямой, кривой линии, плоскости, кривой поверхности или в пространстве.- 330, 479, 503
Координаты на сфере. - 340
Корню спираль - спиралевидная кривая, состоящая из двух симметричных относительно некоторой точки ветвей.- 291
Косинус - одна из тригонометрических функций. Название «косинус» представляет собой сокращение латинского термина complementi sinus (синус дополнения). Знак cos ввел (1748) Л. Эйлер.- 368, 369, 490, 504
Коши, Огюстен Луи (1789-1857) - французский математик. Автор классических курсов математического анализа, оказавших большое влияние на его развитие и строгое обоснование.- 504
Кривизна пространства. - 320
Криволинейная трапеция. - 356
Криволинейные координаты. - 341
Куб - один из пяти типов правильных многогранников; имеет 6 граней (квадратных), 12 ребер, 8 вершин (в каждой вершине сходится 3 ребра).- 296, 309, 501, 502
Кубическая парабола - кривая 3-го порядка, ее уравнение у=х³. - 291
Кубическое уравнение - алгебраическое уравнение 3-й степени.- 327, 475, 476, 503
Лагранж, Жозеф Луи (1736 - 1813) - французский математик и механик. Математические работы относятся к различным вопросам математического анализа и его строгому обоснованию.- 285, 286, 482, 503, 504
Лаплас, Пьер Симон (1749-1827) - французский ученый. Математические труды относятся к разработке теории вероятностей и математического анализа.- 458
Леверье, Урбен Жан Жозеф (1811-1877)-французский астроном.- 372
Легион - наименование в славянской нумерации числа 105 (при счете в «малом числе») или числа 1012 (при счете в «большом числе»),- 275
Лежандр, Адриен Мари (1752-1833) - французский математик. Работал в области теории чисел, математического анализа и геометрии.- 458, 496
Лейбниц, Готфрид Вильгельм (1646-1716) - немецкий ученый.- 264, 327, 368, 485-488, 500, 504
Лемниската - плоская кривая, имеющая вид восьмерки.- 291, 338
Леодр - наименование в славянской нумерации числа 10б (при счете в «малом числе») или числа 1024 (при счете в «большом числе»).- 275
Леонардо Пизанский (Фибоначчи) (ок. 1170 - после 1228) - итальянский математик. Его труды способствовали передаче в Европу достижений математиков Средней Азии и Ближнего Востока.- 267, 278, 325, 327, 503
Ли, Софус (1842-1899) - норвежский математик. Его работы в области теории групп оказали серьезное влияние на развитие многих вопросов современной математики.- 412
Ли алгебра. - 412
Линейное преобразование. -305, 309
Линейное программирование - математическая дисциплина - 285, 444, 445
Линия - одно из основных (неопределяемых) понятий геометрии.- 295
Линия второго порядка. - 336
Лобачевский, Николай Иванович (1792-1856) - русский математик.- 264, 297, 298, 315, 318, 321, 328, 422, 492-494, 504
Лобачевского геометрия - первая геометрическая система, отличная от геометрии Евклида.- 298, 318- 321, 422, 504
Логарифм числа у по основанию а - такое число х, что аx = y или х= loga у. Знак log ввел (1632) Б. Кавальери. Термин «логарифм» возник из сочетания греческих слов logos (здесь - отношение) и arithmos (число). Логарифм у Дж. Непера - их создателя - это вспомогательное число для измерения кратности (степени) отношения двух чисел.- 344, 503
Логарифмическая функция - функция вида y=loga x, где а - положительное число. - 484, 490
Ложного положения метод - метод решения уравнений.- 323
Лудольф, ван Цейлен (1540-1610) - голландский математик. Известен вычислением числа p с 32 десятичными знаками. -452
Ляпунов, Александр Михайлович (1857-1918) - русский математик, академик (с 1901 г.). Основные его работы относятся к теории дифференциальных уравнений, теории вероятностей и гидродинамике.- 458, 498
514
Магницкий, Леонтий Филиппович (1669-1739) - русский математик. Выпущенная им в 1703 г. «Арифметика» была до середины XVIII в. основным учебником математики в России.- 323
Максимин -понятие теории игр. - 469
Максимум и минимум. - 481
«Малое число». - 275
Марков, Андрей Андреевич (1856-1922) - русский математик, академик (с 1896 г.). Научные работы относятся к области теории чисел, теории вероятностей и различным вопросам математического анализа.- 458, 498
Математическая логика. - 392
Математическая статистика. - 458
Математический анализ - часть математики, охватывающая дифференциальное и интегральное исчисления.- 486, 503
Математическое ожидание - понятие теории вероятностей.- 459
Матрица игры - понятие теории игр. - 467
Мебиус, Август Фердинанд (1825-1908) - немецкий математик. Работал в области геометрии. Установил (1858) существование односторонних поверхностей (лист Мебиуса).- 310
Мебиуса лист. - 310
Менелай - древнегреческий ученый, работавший в Александрии в I в. Известны его работы по сферической тригонометрии.- 502
Меридиан - координатная линия на поверхности сферы. - 340
Минимакс - понятие теории игр. - 469
Мириада - наименование в древнегреческой ионийской нумерации числа 104 .- 273
Мнимые числа - числа вида a + bi, где i² = −1, a, b - действительные числа и b ≠ 0. Мнимые числа вида bi называются чисто мнимыми. Обозначение i ввел (1777, в печати 1794) Л. Эйлер. - 503
Многочлен (полином) - алгебраическое выражение, составленное из постоянных величин и переменных x, y, ..., t с помощью операций сложения, вычитания и умножения. Многочлен есть сумма нескольких слагаемых вида Axk yl ...tm, где А - постоянное, а k, l, ..., m - целые положительные числа. - 358, 365, 415
Множеств теория. -374 - 383, 504
Множественная игра - понятие теории игр.- 466
Множество - одно из основных понятий современной математики.- 375
Множество истинности - понятие математической логики.- 392
Моделирование. - 373
Морган, Август де (1806-1871) - английский математик. Основные работы относятся к математической логике. - 395
Моргана правило - один из законов математической логики. - 395
Московский папирус - один из двух дошедших до нашего времени математических папирусов древнего Египта (ок. 2000 до н. э). Содержит 25 задач прикладного характера. Хранится в Москве в Государственном музее изобразительных искусств им. А. С. Пушкина.- 322
Мощность множества - понятие теории множеств.- 381
Надежности теория - математическая дисциплина.- 461-465
Насирэддин Туси, Мухаммед (1201-1274) - азербайджанский астроном и математик. Математические работы относятся к геометрии и сферической тригонометрии. - 476, 503
Натуральные логарифмы. - 344
«Начала» Евклида - научное произведение, написанное в III в. до н. э. древнегреческим математиком Евклидом; содержит основы античной математики: элементарной геометрии, теории чисел, алгебры, общей теории отношений и метода определения площадей и объемов.- 262, 296, 476, 496, 502
Начало координат.- 330
Начальная ордината. - 334
Неевклидова геометрия - геометрическая система, предпосылки которой в том или ином отношении отличны от аксиом обычной геометрии Евклида.- 298 318-321, 492, 494, 504
Независимые события понятие теории вероятностей.- 457
Неопределенное уравнение (или диофантово уравнение) - уравнение, содержащее более одного неизвестного, или система уравнений с числом неизвестных, большим числа уравнений. Обычно интересуются решениями, выраженными целыми или рациональными числами.- 280-286, 502, 503
Непер, Джон (1550-1617) - шотландский математик, изобретатель логарифмов. Его «Описание удивительной таблицы логарифмов» (1614) - сочинение, посвященное логарифмам и их свойствам,- содержало первые логарифмические таблицы.- 503
Неприводимый многочлен. - 415
Несовместные события - понятие теории вероятностей. - 457
Нуль. -276, 277, 287, 503
Нуль-вектор. - 399
Ньютон, Исаак (1643-1727) - английский ученый.- 263, 325-328, 368, 483-485, 486, 488, 502, 504
Ньютона бином. - 476
Ньютона-Лейбница формула - основная формула интегрального исчисления.- 368
Обратное преобразование. - 420
Объем тела. -354, 357, 473, 481,502, 503
Окружность - замкнутая кривая, все точки которой одинаково удалены от одной точки - ее центра.- 336
Октаэдр - один из пяти типов правильных многогранников; имеет 8 граней (треугольных), 12 ребер, 6 вершин (в каждой вершине сходится 4 ребра).- 296, 501, 502
Определение. - 311
Оптимальное решение. - 444
Ордината - одна из декартовых координат точки.- 330
Ось координат. - 330
Ось симметрии. - 307
Отображение. - 376
Отрицание. - 394
Отрицательные числа. -326, 327, 480, 502, 503
515
«Память» - запоминающее устройство электронной вычислительной машины.- 433, 443
Папирусы математические - памятники математической науки древнего Египта, относящиеся ко 2 тысячелетию до н. э.- 262, 272, 322, 501
Парабола - плоская кривая; является геометрическим местом точек, одинаково удаленных от данной прямой и данной точки. - 308, 332, 336, 502
Параллелограмма правило. -398
Параллельное проектирование - геометрическое преобразование.- 304
Параллельный перенос - геометрическое преобразование; является частным случаем движения, при котором все отрезки, соединяющие все соответственные точки, имеют одно и то же направление и одинаковую длину.- 300, 301, 420
Параметр - величина, числовые значения которой позволяют выделить определенный элемент (например, кривую) из множества элементов (кривых) того же рода.- 337
Параметрические уравнения. - 337, 340
Парная игра - понятие теории игр.- 466
Паскаль, Блез (1623-1662) - французский ученый. Математические работы относятся к геометрии, теории чисел и теории вероятностей. Впервые определил и применил для доказательства теорем метод полной математической индукции.- 456, 500, 502, 503
Пачоли, Лука (ок. 1445 - позже 1509) - итальянский математик. Изданный в 1494 г. его труд посвящен арифметическим действиям, алгебраическим уравнениям и их применению к геометрии.- 325
Первообразная - понятие интегрального исчисления.- 368
Переместительный закон - см. Коммутативность.
Перфолента. - 443
«Пи», π - буква греческого алфавита, обозначает в математике число, равное отношению длины окружности к длине ее диаметра. Число π - трансцендентное, оно выражается бесконечной непериодической десятичной дробью. Обозначение ввел (1736) Л. Эйлер. - 452, 474, 478, 501, 503
Пифагор (ок. 580 до н. э.- 500 до н. э.) - древнегреческий математик и философ. В области математики с его именем связано систематическое введение доказательств в геометрию, создание учения о подобии, доказательство теоремы, носящей его имя.- 294, 295
Пифагоров треугольник -279
Пифагорова теорема - теорема геометрии, приписываемая Пифагору: квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов построенных на его катетах.- 294, 501, 502
Плоскость - одно из основных (неопределяемых) понятий геометрии.- 287, 311, 312
Площадь фигуры. -356, 357, 360, 473, 481, 502, 503
Поворот (вращение) - геометрическое преобразование; является частным случаем движения, при котором одна точка О остается неподвижной, а всякая другая точка А переходит в такую точку А', что угол АОА' постоянен для всех точек А. - 301
Подобие - геометрическое преобразование, сохраняющее форму фигур, но, возможно, меняющее их размеры.- 303, 309, 421
Позиционная система счисления - система записи чисел, в которой значение цифры зависит от занимаемого ею места в записи числа.- 276
Позиционный принцип записи чисел. - 265
Показательная функция - функция вида y =ах, где а ¹ 1 - некоторое положительное число.- 344, 345, 369, 484, 490, 504
Поле - понятие современной алгебры.- 413, 417, 496, 504
Полуправильные многогранники. - 293
Полярная ось. -338
Полярные координаты. - 338
Понтрягин, Лев Семенович (р. 1908) - советский математик, академик (с 1958 г.). Научные работы относятся к алгебре, топологии и теории дифференциальных уравнений. - 444
Постулат - суждение, принимаемое без доказательства в качестве исходного положения какой-либо теории. Между постулатом и аксиомой не существует отчетливого различия.- 296
Правильные многогранники. - 296, 297, 501, 502
Правильные многоугольники. -417, 418, 490, 491
Программа (для электронной вычислительной машины).- 432, 434, 437, 443
Проективное преобразование - геометрическое преобразование.- 308, 309, 421
Произведение. -383, 385, 389, 393, 406, 419
Производная - одно из основных понятий математического анализа. Употребляемое ныне обозначение f'(x) ввел Ж. Лагранж (1770).- 364, 365
Простые числа - целые положительные числа, большие, чем единица, и не имеющие других делителей, кроме самих себя и единицы. - 413, 414, 496, 502, 504
Противоречия закон - один из законов математической логики. - 395
Прямая - одно из основных (неопределяемых) понятий геометрии.- 311, 312, 333-336
«Псаммит» - математическое сочинение Архимеда, посвященное изложению способа записи чисел.- 274
Птолемей, Клавдий - древнегреческий ученый, работавший в Александрии во II в. К математике относятся его работы по прямолинейной и сферической тригонометрии и вычислению таблиц синусов.- 263, 502
Пуассон, Симеон Дени (1781-1840) - французский ученый. Математические работы относятся к теории дифференциальных уравнений, теории вероятностей и математическому анализу. -458, 500
Пустое множество. - 387
Равенство фигур - 300, 420, 421
Радиус-вектор. - 402
Раманужан, Сриниваза (1887-1917) - индийский математик.- 353
Распределительный закон - см. Дистрибутивность.
Рассеивания метод - метод решения неопределенных уравнений.- 282
Решение игры - понятие теории игр.- 467, 471
Риман, Георг Фридрих Бернхард (1826-1866) - немецкий математик. Его работы по геометрии, теории чисел и теории аналитических функций оказали большое влияние на развитие математики.- 298, 494, 504
Римана геометрия. -298
Римановы геометрии. - 298, 504
Римские цифры - цифры древних римлян.- 269
516
Самосовершенствующаяся система. - 447
Седловая точка - понятие теории игр.- 470
Середины правило. - 398
Сжатие к прямой - геометрическое преобразование (отображение), при котором каждая точка А переходит в точку А' перпендикуляра, опущенного из точки А на эту прямую, причем отношение расстояния от прямой до A и до A ' постоянно для всех точек А. - 305
Сжатия коэффициент. - 305
Симметрии ось. - 307
Симметрии центр. - 307
Симметрические многочлены. - 425
Симметрия - геометрическое преобразование; различают симметрию относительно точки (см. стр. 301), симметрию относительно прямой (см. стр. 301), симметрию порядка я (см. стр. 304, 423, 424).
Синус - одна из тригонометрических функций. Название «синус» (латинское sinus - пазуха) представляет собой точный перевод на латинский язык арабского слова «джайб», являющегося, по-видимому, искажением санскритского слова «джива», которое буквально переводится как «тетива лука» и которым индийские математики обозначали синус. Знак sin ввел (1748) Л. Эйлер.- 368, 369, 490, 504
Синусоида - плоская кривая, изображающая изменение синуса в зависимости от изменения его аргумента (угла). - 347
Славянская нумерация - алфавитная нумерация, употреблявшаяся в древней Руси до XVII в.- 274, 275
Следствие - понятие математической логики.- 396
Случайное событие - событие, которое может при данных условиях как произойти, так и не произойти и для которого имеется определенная вероятность его наступления.- 452, 453
Случайный процесс - процесс, течение которого может быть различным в зависимости от случая и для которого определена вероятность того или иного его течения. -461
Смешанная стратегия - понятие теории игр.- 468, 471
Событие. -452, 455
Совершенные числа. -325, 382
Сочетательный закон - см. Ассоциативность.
Среднее значение - понятие теории вероятностей.- 459
Стевин, Симон (1548-1620) - нидерландский математик. Ввел в употребление (в Европе) десятичные дроби и отрицательные корни уравнений.- 397, 503
Стратегия - понятие теории игр. - 466
Сумма. -383, 384, 385, 389, 393, 398
Сунь-Цзы - китайский математик III в. Автор «Математического трактата», содержащего сведения о решении неопределенных уравнений.- 503
Сферическая геометрия - математическая дисциплина, изучающая геометрические образы на сфере.- 502, 503
Сферическая тригонометрия - математическая дисциплина, изучающая зависимости между сторонами и углами сферических треугольников, возникающих при пересечении трех больших кругов сферы. - 502
Счетное множество - понятие теории множеств.- 378
Тарталья, Никколо (ок. 1499-1557) - итальянский математик. Его имя связано с разработкой способа решения кубического уравнения.- 327, 503
Теорема - предложение (утверждение), устанавливаемое при помощи доказательства (в противоположность аксиоме).- 313, 411
Тетраэдр - один из пяти типов правильных многогранников; имеет 4 грани (треугольные), 6 ребер, 3 вершины (в каждой вершине сходится 3 ребра).- 296, 501, 502
Техническая кибернетика. - 446
Теэтет - древнегреческий математик начала IV в. до н. э.- 502
Топология - математическая дисциплина, изучающая наиболее общие свойства геометрических фигур - так называемые топологические свойства, т. е. свойства формы и взаимного расположения фигур.- 489
Тор - поверхность, имеющая вид баранки.- 288
Торичелли, Эванджелиста (1608-1647) - итальянский ученый. Математические работы относятся к вычислению площадей большого класса фигур.- 503
Точка - одно из основных (неопределяемых) понятий геометрии.- 295, 311
Тригонометрические функции. -347, 484, 504
Тригонометрия - математическая дисциплина, изучающая тригонометрические функции и их приложения к геометрии.- 263, 478, 502
Трисекция угла - знаменитая задача древности: с помощью циркуля и линейки разделить угол на три части. Задача сводится к построению корня кубического уравнения, что неосуществимо в общем случае с помощью только указанных средств.- 327, 337, 501
Троичная система счисления - система счисления, в которой за основание принимается число «три», так что все числа записываются с помощью только трех цифр: О, 1, 2.- 266, 268
Туэ, Аксель (1863-1922) - норвежский математик. Работы в области теории чисел.- 286
Тьма - наименование в славянской нумерации числа 104 (при счете в «малом числе») или числа 106 (при счете в «большом числе»).- 275
Угловой коэффициент. - 334
Удвоение куба - знаменитая задача древности: с помощью циркуля и линейки построить куб, имеющий объем, вдвое больший объема данного куба. Задача
3 ___
сводится к построению отрезка, численно равного ³√2, что неосуществимо с помощью только указанных средств. - 327, 337, 418, 475, 501
Универсальная управляющая машина. - 445
Управляющая система. - 441
Управляющее устройство - одно из пяти основных устройств быстродействующей электронной вычислительной машины.- 434
Уравнение - аналитическая запись задачи о разыскании значений аргументов, при которых значения двух данных функций равны. Важнейший класс уравнений - алгебраические уравнения, исследование которых привело к созданию алгебры.- 324
Условие - понятие математической логики.- 396
517
Федоров, Евграф Степанович (1853-1919) - русский ученый, академик (с 1919 г.). Для математики имеют важное значение его исследования по геометрической структуре кристаллов.- 423
Ферма, Пьер (1601-1665) - французский математик.- 263, 286, 329, 456, 481, 482, 502, 503
Ферма великая теорема - утверждение о том, что уравнение xn +yn =zn, где n - целое число, большее двух, не имеет решений в целых положительных числах. В общем случае доказательство не найдено.- 286, 482
Ферма малая теорема. - 482
Ферма числа. - 482
Феррари, Лодовико (1522-1565) - итальянский математик. Нашел способ (опубл. в 1545 г.) решения уравнений 4-й степени.- 327, 503
Ферро, Даль Ферро, Сципион (1465-1526) - итальянский математик. С его именем связано открытие правила решения кубических уравнений специального вида.- 327, 503
Фибоначчи - см. Леонардо Пизанский.
Флюксий метод - ранняя форма дифференциального и интегрального исчислений, возникшая в трудах И. Ньютона.- 484
Функциональная зависимость. - 342, 503
Функция - одно из основных понятий математики, выражающее зависимость одних переменных величин от других. Общепринятое ныне обозначение произвольной функции f (х) ввел (1734) Л. Эйлер.- 342-352, 503, 504
Хайям, Омар (ок. 1040-1123) - среднеазиатский поэт, математик и философ.- 327, 474-476,. 503
Хинчин, Александр Яковлевич (1894-1959) - советский математик, член-корреспондент Академии наук СССР (с 1939 г.). Работы относятся к теории вероятностей и теории чисел.- 461
ал-Хорезми, Мухаммед бен Муса (ок.780-ок.850) - среднеазиатский математик и астроном. Автор трактатов, переведенных в XII в. с арабского на латинский язык, по которым в Европе познакомились с индийской позиционной десятичной системой счисления и алгеброй как самостоятельной областью математики.- 324-326, 503
Цена игры - понятие теории игр. - 467
Центральное проектирование - геометрическое преобразование.- 308
Центроид.- 406-408
Цепная линия - линия, по которой провисает тяжелая нерастяжимая нить.- 291
Циклоида - линия, являющаяся следом точки окружности, катящейся без скольжения по прямой.- 291
Чебышев (произносится Чебышёв), Пафнутий Львович (1821-1894) - русский математик, академик (с 1859 г.).- 264, 458, 459, 496-498, 504
Чисел теория - часть математики, посвященная изучению закономерностей, справедливых для целых чисел.- 481, 489, 491, 497, 501, 504
Число «e», неперово число - такое число, что график функции y=ex пересекает ось ординат под углом 45°; может быть определено так же как предел, к которому стремится выражение (1+1/n)n при неограниченном возрастании n; является основанием натуральных логарифмов. Обозначение (e) для этого числа ввел (1736) Л. Эйлер.- 344
Шмидт, Отто Юльевич (1891-1956) - советский ученый, академик (с 1935 г.). Математические работы относятся к теории групп,- 426
Штифель, Михаил (1486-1567) - немецкий математик. При решении квадратных уравнений один из первых стал употреблять отрицательные числа, сформулировал правила действия над показателями степеней. - 325
Шухов, Владимир Григорьевич (1835-1939) - советский ученый, почетный академик (с 1929 г.). По его конструкции сооружено множество мачт, башен, антенн в виде однополостного гиперболоида вращения (башни Шухова). - 290
Эвольвента круга - линия, описываемая концом гибкой нерастяжимой нити, сматываемой с круга. - 291
Эйлер, Леонард (1707-1783) - математик, механик и физик, работавший более 30 лет в Петербургской Академии наук. - 267, 286, 325, 327, 349, 481, 482, 488-491, 503, 504.
Эйлера диаграмма. - 385
Эйлера теорема о многогранниках. - 489, 490
Экватор. - 340
Экваториальная плоскость. - 340
Эквивалентные высказывания. - 393
Экономическая кибернетика. - 445
Электронная вычислительная машина. - 432
Эллипс - плоская овальная кривая; является геометрическим местом точек, сумма расстояний которых до двух данных равна постоянной величине.- 288, 291, 307, 308, 336, 337, 502
Эллипсограф.- 337
Экстремум - термин, употребляемый для объединения понятий максимума и минимума функции.- 474, 481, 503
Эллиптическая геометрия. - 298
«Эрлангенская программа». - 422, 424
Детская Энциклопедия - Список томов
ДЭ, том 2 Содержание